【论文解读】deepseek系列：《Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention》

论文链接

论文详细解析：Native Sparse Attention

硬件对齐与原生可训练的稀疏注意力机制

本文提出了一种全新的稀疏注意力机制（NSA），其核心目标是在保证长上下文建模能力的同时，实现高效的计算和端到端训练。

---

1. 摘要 (Abstract)

• 背景与问题：
  随着大语言模型对长文本、复杂推理和多轮对话的需求增加，传统全注意力（Full Attention）机制面临计算量急剧增加的瓶颈。虽然稀疏注意力通过只计算关键的查询-键对来降低计算复杂度，但大多数现有方法仅适用于推理阶段，且难以在训练时实现端到端优化。

• 提出方案：NSA
  NSA（Native Sparse Attention）是一种原生可训练的稀疏注意力机制，结合了两大创新：

  1. 硬件对齐的算法设计： 通过平衡算术强度，并针对现代硬件（如Tensor Core）进行优化，从而实现高效推理。
  2. 端到端训练支持： 设计了适用于训练的可微分操作，使得整个稀疏注意力模块能够在预训练中直接优化，而无需后期剪枝或其他后处理。

• 核心思路：
  NSA 利用动态分层策略，将输入序列转换为更紧凑的信息表示，既保留全局上下文信息，又能捕捉局部细节。其主要策略包括：

  • Token 压缩（Compression）： 对连续的 tokens 进行块级聚合，生成粗粒度表示。
  • Token 选择（Selection）： 针对每个查询，选取最相关的细粒度 tokens。
  • 滑动窗口（Sliding Window）： 保持局部最近 tokens 信息，确保局部细节不丢失。
    

---

2. 引言 (Introduction)

• 长上下文建模的重要性：
  现代大模型需要处理超长文本（如代码库、长篇对话、复杂推理文本等），而全注意力的计算复杂度随着序列长度呈平方级增长，极大影响了推理和训练效率。

• 现有方法的不足：

  • 推理阶段的稀疏化： 许多方法（如 KV-cache 剪枝、固定窗口策略）只在推理时应用稀疏策略，但在预训练时仍依赖全注意力。
  • 非可微分操作： 部分方法使用离散操作（如聚类、哈希）导致无法在训练过程中传递梯度，从而限制了稀疏模式的自适应学习。

• 面临的两大挑战：

  1. 硬件对齐的推理加速： 如何设计符合硬件调度和内存访问模式的算法，从而将理论上的计算节省转化为实际速度提升。
  2. 训练感知的设计： 需要构造可微分的稀疏操作，使模型能够在训练时自然学习到最优的稀疏模式。

---

3. 方法论 (Methodology)

3.1 背景知识

• 标准注意力机制：
  给定查询 $q_t$、键 $k_{1:t}$ 以及值 $v_{1:t}$，传统注意力计算公式为：
  $$o_t=\text{Attn}(q_t,k_{1:t},v_{1:t})=\sum _{i=1}^t\frac{e^{q_t^{\top }{k}_i/\sqrt{d_k}}}{{\sum }_{j=1}^t{e}^{q_t^{\top }{k}_j/\sqrt{d_k}}}{v}_i.$$
  随着序列长度 (t) 增大，计算复杂度和内存访问量急剧上升。

• 算术强度（Arithmetic Intensity）：
  指计算操作与内存访问的比率。训练和预填充阶段通常计算密集，而自回归解码阶段则受限于内存带宽。NSA正是针对不同阶段优化设计的。

3.2 NSA整体框架

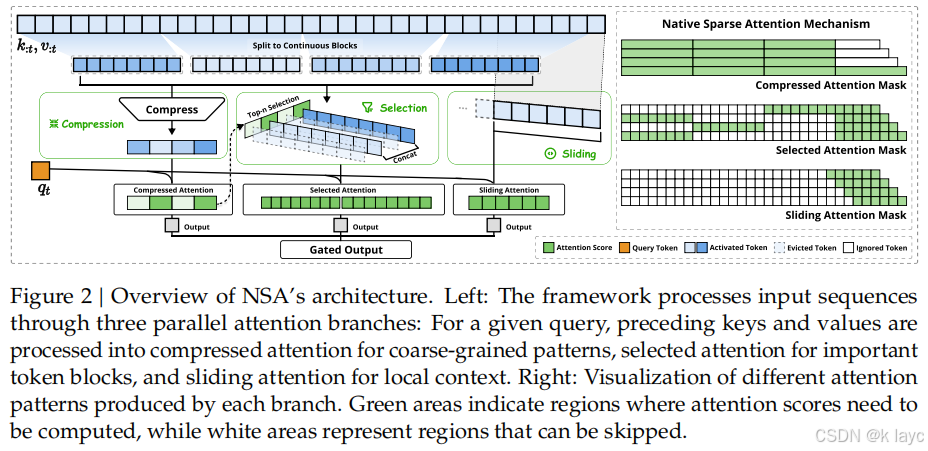
• 动态映射表示：
  NSA 不再直接使用全序列的键和值，而是通过映射函数 $f_K$ 与 $f_V$ 动态构造更紧凑的表示：
  $${\tilde{k}}_t=f_K(q_t,k_{1:t},v_{1:t}),{\tilde{v}}_t=f_V(q_t,k_{1:t},v_{1:t}).$$

• 多分支设计：
  将映射策略划分为三个分支 C = { cmp , slc , win } C = \{\text{cmp}, \text{slc}, \text{win}\} C={cmp,slc,win}：

  • 压缩（Compression，cmp）：
    将连续的 tokens 分成块，通过带位置编码的MLP将每个块聚合成一个压缩表示。
    数学上：
    k ~ cmp , t = f cmp K ( k 1 : t ) = { ϕ ( k i + 1 : i + l ) ∣ 1 ≤ i ≤ ⌊ ( t − l ) / d ⌋ } , \tilde{k}_{\text{cmp}, t} = f^K_{\text{cmp}}(k_{1:t}) = \{ \phi(k_{i+1:i+l}) \mid 1 \le i \le \lfloor (t-l)/d \rfloor \}, k~cmp,t​=fcmpK​(k1:t​)={ϕ(ki+1:i+l​)∣1≤i≤⌊(t−l)/d⌋},
    其中 $l$ 为块长度，$d$ 为滑动步长，$\varphi$ 为可学习的映射函数。

  • 选择（Selection，slc）：
    通过计算压缩分支得到的注意力分数，对输入序列的块进行评分，选出最关键的几个块以获得细粒度信息。
    具体做法是：

    1. 将输入序列分块；
    2. 利用压缩分支得到的中间注意力分数 $p_{\text{cmp},t}$ 推导出选择块的重要性 $p_{\text{slc},t}$；
    3. 按重要性排序，选择 top-$n$ 块，然后拼接这些块内的原始 tokens，得到细粒度表示 ${\tilde{k}}_{\text{slc},t}$。

  • 滑动窗口（Sliding Window，win）：
    为确保局部上下文信息不丢失，直接选取最近 (w) 个 tokens 作为滑动窗口表示，即：
    $${\tilde{k}}_{\text{win},t}=k_{t-w:t}.$$

• 融合策略：
  最终的注意力输出是各分支结果的加权和：
  $$o_t^{\ast }=\sum _{c\in C}{g}_{c,t}\cdot \text{Attn}(q_t,{\tilde{k}}_t^{(c)},{\tilde{v}}_t^{(c)}),$$
  其中 $g_{c,t}$ 是通过一个MLP和sigmoid函数计算得到的门控分数，用于平衡各分支的重要性。

3.3 详细算法设计

3.3.1 Token 压缩

• 目标：
  将长序列中的连续 tokens 压缩为少量的块级表示，捕捉全局语义同时降低计算量。

• 实现方法：

  • 设定块长度 $l$ 和滑动步长 $d$（通常 $d<l$ 以减少信息碎片化）；
  • 对每个块使用带位置编码的MLP $\varphi$ 聚合块内的 keys（和对应的 values），生成压缩表示。

3.3.2 Token 选择

• 目的：
  在压缩过程中可能丢失关键的细粒度信息，因此需要在原始序列中选取最具代表性的 tokens。

• 步骤：

  1. 块划分： 将输入序列划分为若干连续块。
  2. 计算重要性： 利用压缩分支产生的注意力分数 $p_{\text{cmp},t}$ 推导出各块的重要性评分 $p_{\text{slc},t}$；
     • 若压缩块与选择块采用相同分割方式，直接使用 $p_{\text{cmp},t}$；
     • 否则，通过空间加权平均获得选择块评分。
  3. 选取 Top-$n$ 块： 根据评分选择最重要的 $n$ 个块，并将这些块内的 tokens 拼接起来形成细粒度表示 ${\tilde{k}}_{\text{slc},t}$。

3.3.3 Sliding Window

• 作用：
  直接保留局部最近 tokens 信息，防止模型因过度依赖全局信息而忽略局部细节。

• 实现：

  • 设定窗口大小 $w$，直接提取序列中最近 $w$ 个 tokens 作为滑动窗口分支输入，形成 ${\tilde{k}}_{\text{win},t}$ 与 ${\tilde{v}}_{\text{win},t}$。

分支融合

各分支独立计算注意力后，通过门控机制按比例融合，既确保全局信息的捕捉，也保留了细粒度局部信息。

3.4 内核设计 (Kernel Design)

• 目标：
  实现与 FlashAttention 相媲美的速度，尤其是在训练和预填充阶段，同时兼顾解码时的内存访问效率。

• 关键优化措施：

  1. 组中心数据加载：
     针对基于 GQA（Grouped-Query Attention）的架构，在每个内循环中将同一组内所有查询头加载到共享存储器（SRAM）中，减少重复数据传输。
  2. 共享 KV 获取：
     在内循环中依次加载连续的键值块，从而充分利用内存访问的连续性，最大化 Tensor Core 的利用率。
  3. 网格调度（Grid Loop）：
     利用 Triton 的网格调度，将查询块的外循环并行化，平衡各个 Streaming Multiprocessor 的负载。

• 效果：
  得益于这些优化，NSA 在长序列（例如64k tokens）下的前向传播速度可达到 9 倍加速，反向传播速度可达 6 倍加速，并且在解码时由于内存访问量大幅降低，实现近似线性的加速效果。

---

4. 实验 (Experiments)

4.1 预训练设置

• 模型架构：

  • 采用27B参数的Transformer模型，结合了 Grouped-Query Attention（GQA）和 Mixture-of-Experts（MoE）结构。
  • MoE 部分采用 DeepSeekMoE 设计，拥有72个专家和2个共享专家，进一步提升模型能力。

• 训练数据与策略：

  • 在270B tokens的8k长度文本上预训练；
  • 随后在32k长度文本上继续训练，实现长上下文适应，保证模型在多种任务上的泛化能力。

• 关键参数配置：

  • 压缩块大小 $l=32$，滑动步长 $d=16$；
  • 选择块大小 $l^{\prime }=64$，选取块数 $n=16$（包括固定选取初始块和局部块）；
  • 滑动窗口大小 $w=512$。

4.2 与基线方法的比较

• 对比方法：

  • 全注意力模型（Full Attention）；
  • 其他先进的稀疏注意力方法，如 H2O、InfLLM、Quest、Exact-Top 等。

• 评估任务：

  • 涵盖知识问答（MMLU、CMMLU）、推理（BBH、GSM8K、MATH、DROP）以及代码生成（MBPP、HumanEval）等多个方面。

• 实验结果：

  • NSA 在大部分指标上均超越或匹配全注意力模型，尤其在长上下文任务中（例如64k上下文的 needle-in-a-haystack 检索任务）表现出完美准确率；
  • 在链式思考（Chain-of-Thought）推理任务中，经过监督微调后，NSA 在 AIME 数学推理测试中也显著优于全注意力基线。

4.3 效率评估

• 训练速度：

  • 基于 Triton 实现的 NSA 内核在前向传播和反向传播上均展示出显著加速，前向最高可达9倍，反向最高可达6倍（在64k序列下）。

• 解码速度：

  • 由于仅需加载压缩 tokens、选取 tokens 与局部窗口 tokens，总体内存访问大幅减少，使得解码速度随着序列长度的增长近似呈线性提升（64k上下文下加速比可达11.6倍）。

---

5. 效率分析 (Efficiency Analysis)

• 内存访问优势：
  NSA 通过精心设计的块级选择和连续内存加载策略，极大降低了解码过程中 KV 缓存的加载量，这对于内存带宽受限的自回归解码阶段尤为关键。

• 算术强度提升：
  内核设计优化了数据传输与计算的平衡，使得模型在计算密集和内存密集阶段均能高效运行，实现整体计算资源的最大化利用。

---

6. 讨论 (Discussion)

6.1 替代 Token 选择策略的挑战

• 聚类方法的局限性：

  • 例如 ClusterKV 等基于聚类的方法，在动态聚类、负载均衡以及周期性重聚类时会引入较大计算开销；
  • 在 MoE 等场景下，还可能因专家间负载不均而导致效率下降。

• 启发式选择的不足：

  • 基于非参数启发式方法（如 Quest 中的策略）虽然简单，但召回率较低，导致关键 token 可能被遗漏，从而影响整体性能。

• NSA 的优势：

  • 采用基于注意力分数的块级选择方式，在保持硬件友好性（连续内存访问）的同时，确保了重要细粒度信息的捕捉。

6.2 注意力分布的可视化

• 观察结果：
  • 通过对预训练的全注意力模型注意力图进行可视化，发现注意力分数呈现明显的块状聚类现象，即相邻的 tokens 往往具有相似的重要性。
• 启发：
  • 这一现象为 NSA 的块级选择策略提供了直观依据，即在连续块内进行聚合和选择能够更好地保留关键信息，同时降低计算量。

---

7. 相关工作 (Related Works)

论文中将现有稀疏注意力方法大致分为三类：

1. 固定稀疏模式（Fixed Sparse Pattern）：

   • 如 Sliding Window 方法，只在局部窗口内计算注意力，虽然降低了计算量，但在捕捉全局信息方面存在局限。

2. 动态 Token 剪枝（Dynamic Token Pruning）：

   • 例如 H2O、SnapKV，通过在推理时动态剪枝不重要的 tokens 来减少 KV 缓存，但训练阶段仍然依赖全注意力，且不支持端到端优化。

3. 查询感知选择（Query-Aware Selection）：

   • 包括 Quest、InfLLM、HashAttention、ClusterKV 等方法，通过计算查询与键之间的相似度来选取关键 tokens，但往往依赖非可微分操作，难以在训练中优化。

NSA 则突破了上述方法的局限，构建了一种既能支持高效推理又能端到端训练的稀疏注意力架构。

---

8. 结论 (Conclusion)

• 总结：

  • NSA 提出了一种硬件对齐且原生可训练的稀疏注意力机制，通过分层策略（Token 压缩、Token 选择和 Sliding Window）实现了对长上下文的高效处理。
  • 实验结果显示，NSA 在多项基准任务上不仅能够与全注意力模型持平，还在长上下文和复杂推理任务上展现出更优的性能，同时在训练与推理速度上具有显著优势。

• 未来展望：

  • NSA 的成功为在硬件友好性与模型高效性之间取得平衡提供了新思路，也为后续在长上下文大模型设计中的稀疏注意力机制研究指明了方向。

---