方格取数问题【网络流24题】

最新推荐文章于 2024-05-09 15:54:38 发布

原创最新推荐文章于 2024-05-09 15:54:38 发布 · 226 阅读

0 ·

CC 4.0 BY-SA版权

网络流专栏收录该内容

12 篇文章

订阅专栏

本文深入探讨了最小割算法在网络流问题中的应用，通过一个具体题目实例，讲解了如何利用最小割算法解决实际问题。文章详细介绍了算法的实现过程，包括构建网络流图、使用前向星结构进行加边操作、BFS构建分层图、DFS寻找增广路径等关键步骤，并最终实现了Dinic算法求解最大流，从而得到最小割。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：https://www.luogu.org/problem/P2774

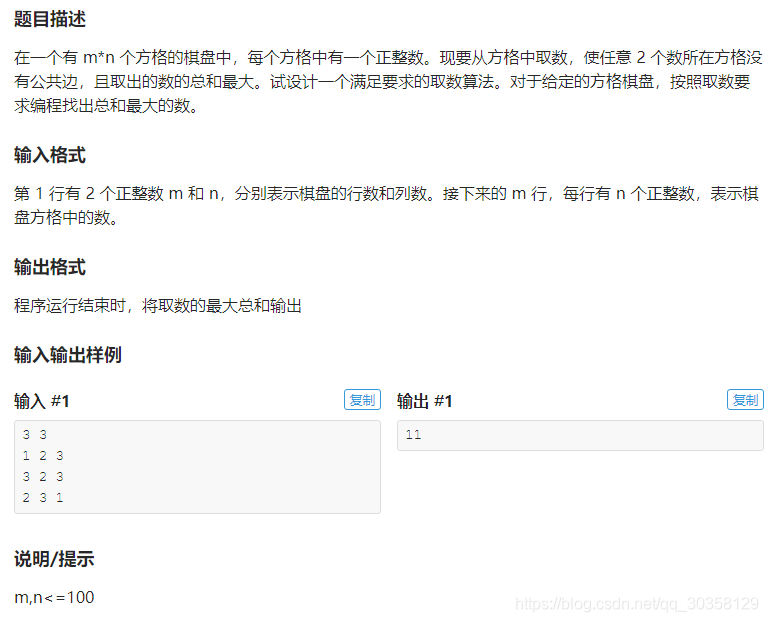
最小割建图。

先对格子分为黑白格，类似国际象棋。

然后S连黑，边权为黑点点权。

每个黑连周围4个白，边权为inf。

每个白连T，边权为白点点权。

#include <bits/stdc++.h>
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
using namespace std;
const int N = 1e4+100;
int n,m,S,T,tot;
int head[N];
struct node{
    int v,cap,nxt;
}edge[int(2e5+100)];
int cur[N],deep[N];
void ae(int u,int v,int cap){  //前向星加边
    edge[++tot] = node{v,cap,head[u]};
    head[u] = tot;

    edge[++tot] = node{u,0,head[v]};
    head[v] = tot;
}
bool bfs(){  //构建分层图
    memset(deep,-1,sizeof(deep));  //-1表示未访问
    queue<int>q;
    q.push(S);
    deep[S] = 0;
    while(!q.empty()){
        int u = q.front();
        for(int i = head[u]; ~i;i = edge[i].nxt){
            int v = edge[i].v;
            if(deep[v]==-1&&edge[i].cap>0){
                q.push(v);
                deep[v] = deep[u]+1;
                if(v==T) return 1;   //提前退出
            }
        }
        q.pop();
    }
    return 0;
}
int dfs(int u,int f){  //寻找增广网
    int flow = 0,d;
    if(u==T||f==0) return f;
    for(int &i = cur[u]; ~i;i = edge[i].nxt){ //当前弧优化
        int v = edge[i].v;
        if(deep[v]>deep[u]&&edge[i].cap>0&&(d=dfs(v,min(f,edge[i].cap)))){
            edge[i].cap -= d;
            edge[i^1].cap += d;
            f -= d;
            flow += d;
            if(!f) break;
        }
    }
    if(flow==0) deep[u] = -1;  //删除无法增广的点
	return flow;
}
int dinic(){
    int ans = 0;
    while(bfs()){
        memcpy(cur, head, sizeof(head));  //重置cur数组
        ans += dfs(S,1e9);
    }
    return ans;
}
int v[N],sum;
int main() {
    //freopen("a.txt","r",stdin);
    ios::sync_with_stdio(0);
    cin>>n>>m;
    memset(head,-1,sizeof(head));  //head初始化-1
    tot = -1;   //边从0开始编号
    rep(i, 0, n-1)
        rep(j, 0, m-1) {
            cin>>v[i*m+j];
            sum += v[i*m+j];
        }
    S = n*m;
    T = n*m+1;
    rep(i, 0, n-1)
        rep(j, 0, m-1) {
            int u = i*m+j;
            if((i+j)%2==0) {
                ae(S,u,v[u]);
                if(i>0) ae(u,u-m,1e9);
                if(i<n-1) ae(u,u+m,1e9);
                if(j>0) ae(u,u-1,1e9);
                if(j<m-1) ae(u,u+1,1e9);
            }
            else ae(u,T,v[u]);
        }
    cout<<sum-dinic()<<endl;
    return 0;
}