软渲染器(Directx11)一之向量,顶点,矩阵

最新推荐文章于 2025-05-21 09:05:42 发布

原创最新推荐文章于 2025-05-21 09:05:42 发布 · 1.5k 阅读

1 ·

CC 4.0 BY-SA版权

软渲染引擎(SoftRasterizer)的实现专栏收录该内容

6 篇文章

订阅专栏

本文介绍了3D渲染引擎中向量、顶点和矩阵的基本表示方法，并提供了具体的代码实现细节，包括向量和顶点的定义、矩阵的表示方式、向量间的点乘和叉乘运算、向量规格化等，最后还讲解了向量和点乘以矩阵及矩阵乘法的具体计算过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最近我完成了一个3D软件光栅器，也就是用CPU运行的小型3D渲染引擎，下面我就分为几个章节分别说下我实现的思路

一,向量,顶点,矩阵的表示。

(1) 向量,顶点

通常我们的向量和顶点都是用(x,y,z)表示，但是在3D图形学里，我们用(x,y,z,w)表示,那么在3D图形学里顶点和向量有什么区别呢?

在3D图形学里,顶点(Vertex)用(x,y,z,1.0)表示,而向量用(x,y,z,0.0)表示,为什么会这样呢?其实原因很多，第四个参数的引入可以让我们实现仿射变换,可以让我们在透视投影变换后用第四个参数保存相机空间的Z值，反正好处非常多，详细内容可参见http://blog.youkuaiyun.com/popy007/article/details/1797121

或者《Introduction+to+3D+Game+Programming+with+DirectX+11》第三章。

(2) 矩阵

在3D图形学里，我们用到的矩阵为4x4矩阵，用C++的二维数组来表示为 float[4][4], 如下面图所示：

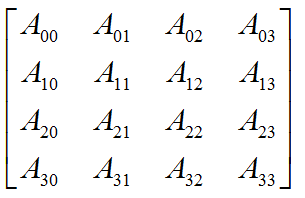
二,向量，顶点，矩阵的定义:

(1) 向量,顶点

代码实现:

/*----------------一，向量和顶点--------------*/
struct Vector
{
	float x, y, z, w;
};

typedef Vector Point;

//构造一个顶点
Point BuildPoint(float x, float y, float z)
{
	Point mPoint;
	mPoint.x = x;
	mPoint.y = y;
	mPoint.z = z;
	mPoint.w = 1.0f;
	return mPoint;
}

//构造一个向量
Vector BuildVector(float x, float y, float z)
{
	Vector mVector;
	mVector.x = x;
	mVector.y = y;
	mVector.z = z;
	mVector.w = 0.0f;
	return mVector;
}

(2) 矩阵

代码实现:

/*------------------二，矩阵-------------------*/
struct Matrix
{
	float ma[4][4];
};

三,向量，顶点，矩阵的运算

(1) 向量点乘:

假设有两个向量Vector1 (x1,y1,z1,0) 和Vector2 (x2,y2,z2,0),公式如下:

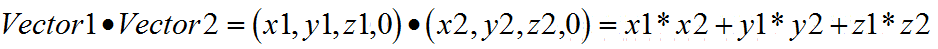
代码实现:

//向量点乘(包括点和向量)
float VectorDotProduct(const Vector* v1, const Vector* v2)
{
	float sum;
	sum = v1->x*v2->x + v1->y*v2->y + v1->z*v2->z + v1->w*v2->w;

	return sum;
}

(2) 向量叉乘:

假设有两个向量Vector1 (x1,y1,z1,0) 和Vector2 (x2,y2,z2,0),公式如下:

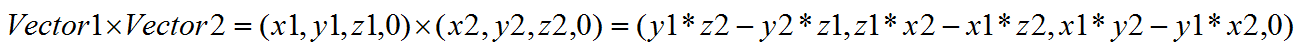
代码实现:

//向量叉乘
Vector VectorCrossProduct(const Vector* v1, const Vector* v2)
{
	Vector crossVector;
	float x1, y1, z1, x2, y2, z2;
	x1 = v1->x;
	y1 = v1->y;
	z1 = v1->z;
	x2 = v2->x;
	y2 = v2->y;
	z2 = v2->z;
	crossVector.w = 0.0f;
	crossVector.x = y1*z2 - z1*y2;
	crossVector.y = z1*x2 - x1*z2;
	crossVector.z = x1*y2 - y1*x2;
	return crossVector;
}

(3) 向量规格化:

假设有存在一个向量Vector(x1,y1,z1,0)，规格化后变为(x2,y2,z2,0),则x2*x2+y2*y2+z2*z2=1, 公式如下:

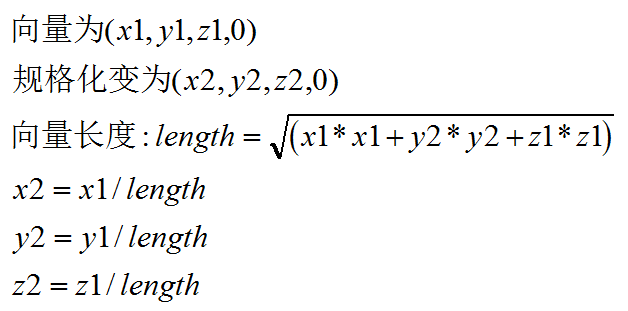
代码实现:

//向量规格化
void VectorNormalize(Vector* v)
{
	float length =(float)sqrt(v->x*v->x + v->y*v->y + v->z*v->z);
	v->x = v->x / length;
	v->y = v->y / length;
	v->z = v->z / length;
}

(4) 向量相减:

假设有两个向量Vector1 (x1,y1,z1,0) 和Vector2 (x2,y2,z2,0),公式如下:

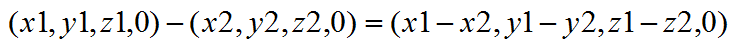
//向量相减,左减去右
Vector VectorSubtract(const Vector* v1, const Vector* v2)
{
	Vector vec;
	vec.x = v1->x - v2->x;
	vec.y= v1->y - v2->y;
	vec.z = v1->z - v2->z;
	vec.w = 0.0f;

	return vec;
}

(5) 向量或者点乘以矩阵:

假设有一个向量或者顶点为(x,y,z,w),则顶点或者向量乘以矩阵的运算公式为

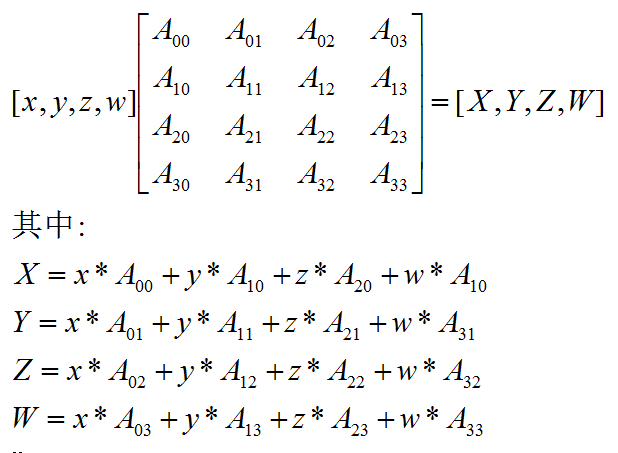
如果为顶点，也就是(x,y,z,1), 则运算公式为:

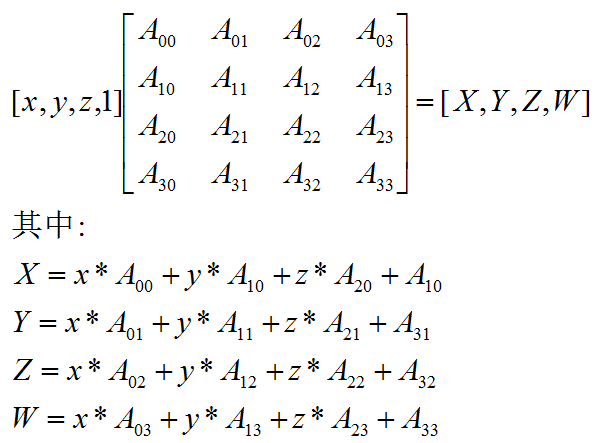
如果为向量，也就是(x,y,z,0), 则运算公式为:

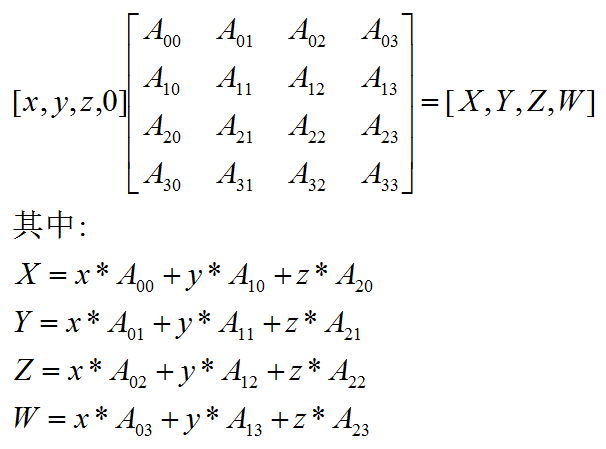
代码实现:

//向量进行矩阵变换, 对于不改变内容的函数形参加个const
void VectorTransform(Vector* PointPtr, const Matrix* MaPtr)
{
	if (PointPtr == nullptr || MaPtr == nullptr)
	{
		return;
	}
	else
	{
		//不能在中途改变点的值在用改变的点的值去计算，所以先保存顶点的XYZW值先
		float x = PointPtr->x;
		float y = PointPtr->y;
		float z = PointPtr->z;
		float w = PointPtr->w;

		//具体乘法,X
		PointPtr->x = x*MaPtr->ma[0][0] + y*MaPtr->ma[1][0] + z*MaPtr->ma[2][0] + w*MaPtr->ma[3][0];

		//具体乘法,Y
		PointPtr->y = x*MaPtr->ma[0][1] + y*MaPtr->ma[1][1] + z*MaPtr->ma[2][1] + w*MaPtr->ma[3][1];

		//具体乘法,Z
		PointPtr->z = x*MaPtr->ma[0][2] + y*MaPtr->ma[1][2] + z*MaPtr->ma[2][2] + w*MaPtr->ma[3][2];

		//具体乘法,W
		PointPtr->w = x*MaPtr->ma[0][3] + y*MaPtr->ma[1][3] + z*MaPtr->ma[2][3] + w*MaPtr->ma[3][3];
	}
}

(6) 矩阵乘以矩阵:

假设有两个矩阵A和B，A*B得到C矩阵

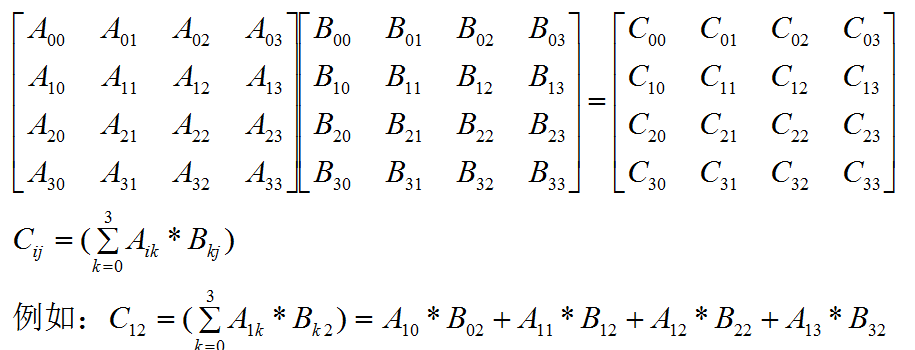
代码实现:

//矩阵乘法
Matrix MatrixMultiply(const Matrix* ma1, const Matrix* ma2)
{
	Matrix matrix;

	//清除为0
	ZeroMemory(&matrix, sizeof(matrix));

	//矩阵乘法
	for (int i = 0; i < 4; ++i)
	{
		for (int j = 0; j < 4; ++j)
		{
			for (int k = 0; k < 4; ++k)
			{
				matrix.ma[i][j] += ma1->ma[i][k] * ma2->ma[k][j];
			}
		}
	}
	return matrix;
}