【GNN】WL-test：GNN 的性能上界

今天学习斯坦福大学同学 2019 年的工作《HOW POWERFUL ARE GRAPH NEURAL NETWORKS?》，这也是 Jure Leskovec 的另一大作。

我们知道 GNN 目前主流的做法都是通过迭代地对邻居进行聚合（aggreating）和转换（transforming）来更新节点的表示向量。而在这篇文章中，本文作者提出了一个可以用于分析 GNN 能力的理论框架，通过对目前比较流行的 GNN 变体（如 GCN、GraphSAGE 等）进行分析，其结果表明目前的 GNN 变体甚至无法区分某些简单的图结构。

本文作者设计了一个简单的架构 GIN（Graph Isomorphism Network），并证明该架构在目前所有 GNN 算法中最具表达能力，并且具有与 Weisfeiler-Lehman 图同构测试一样强大的功能。

读完这段介绍大家可能会有多疑问，包括但不限于：

1. 为什么 GCN、GraphSAGEE 无法区分简单的图结构？
2. 分析 GNN 捕获图结构的能力的理论框架是什么？
3. Weisfeiler-Lehman 图同构测试是什么？
4. 为什么提出的 GIN 要与 Weisfeiler-Lehman 图同构测试进行比较？

接下来，我们带着问题来阅读本篇文章。

1.Introduction

GNN 的许多变体都采用了不同的邻域聚合图级别的池化方案，虽然这些变体在节点分类、连接预测和图分类等任务中取得了 SOTA，但是这些 GNN 的设计主要是基于经验而谈，并没有很好的理论基础来分析 GNN 的性质和局限性。

于是，作者提出了一个理论框架用于分析 GNN 及相关变体的表达能力和区分不同图结构的表现力。该框架的灵感来源于 Weifeiler-Lehman 图同构测试（以下简称 WL-test），WL-test 非常强大，其可用于区分各种图结构。与 GNN 类似，WL-test 可以通过聚合邻居节点的特征向量来迭代给定的特征向量，但目前的 GNN 的表达能力都不如 WL-test。WL-test 之所以那么强主要原因在于单射聚合更新（injective aggregation update），所以如果要想获得与 WL-test 一样强的表现力，首先考虑对 GNN 的聚合方案对单射函数进行建模。

本文有以下贡献：

1. 证明出 WL-test 是 GNN 的表达能力上限；
2. 提出了一个可以用于分析 GNN 能力的理论框架；
3. 设计了聚合函数和读出函数，使得 GNN 可与 WL-test 一样强大；
4. 构建了一个与 WL-test 一样强大的架构——GIN；

2.Weisfeiler-Lehamn

为了让大家无痛学习，我们先写介绍一下 WL-test。

2.1 Graph Isomorphism

先来介绍下什么是同构图。

简单来说，如果图 $G_1$ 和 $G_2$ 的顶点和边数量相同，且边的连接性相同，则可以称这两个图为同构的。也可以认为，$G_1$ 的点是由 $G_2$ 中的点映射得到。

举一个简单例子，判断下面两个图是否是同构的：

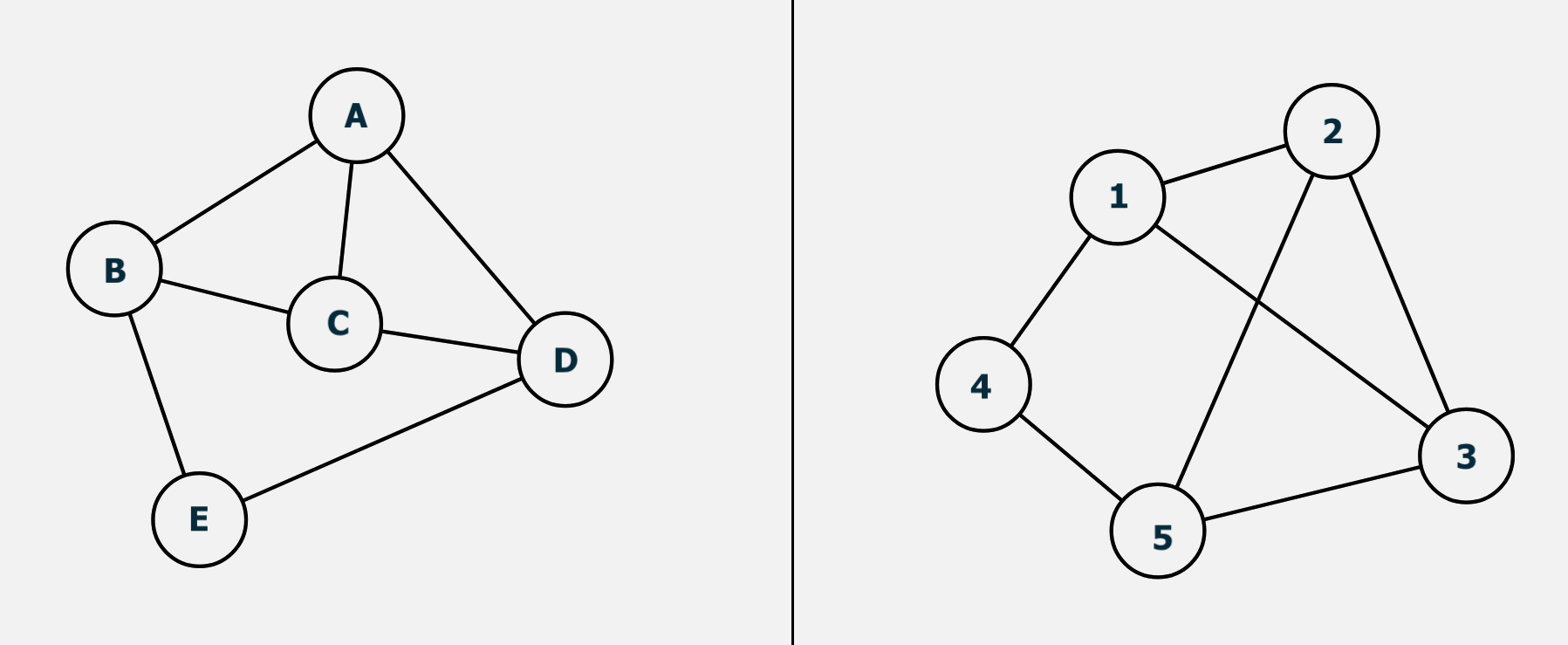
其实上面两张图是同构的，映射关系为：$A-3;B-1;C-2;D-5;E-4$。

这个还算比较简单，但是如果节点和边的数量都增加了，可能就没法一眼看出，更别说真实社交网络中几百万节点，几千条万条边的情况了。

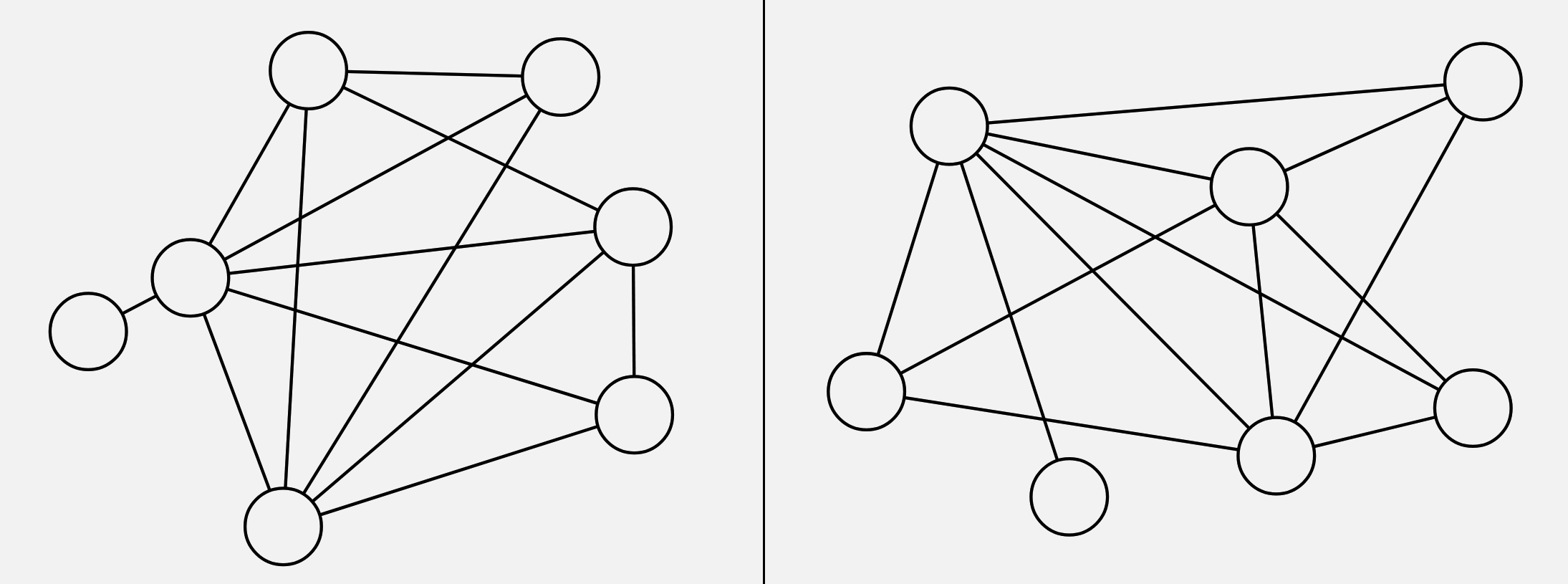
简单介绍下为什么要计算图同构：我们在分析社会网络、蛋白质、基因网络等通常会考虑彼此间的相似度问题，比如说，具有相似结构的分子可能具备相似的功能特性，因此度量图的相似度是图学习的一个核心问题。

而图同构问题通常被认为是 NP 问题，目前最有效的算法是 Weisfeiler-Lehman 算法，可以在准多项式时间内进行求解。

2.2 1-dimensional

WL 算法可以是 K-维的，K-维 WL 算法在计算图同构问题时会考虑顶点的 k 元组，如果只考虑顶点的自身特征（如标签、颜色等），那么就是 1-维 WL 算法。

介绍下 1-维 WL 算法，首先给出一个定义：

多重集（Multiset）：一组可能重复的元素集合。例如：{1,1,2,3}就是一个多重集合。

Nino 大佬在她的论文${}^{[2]}$中给出了一个很经典很形象的例子（不过要注意，这个例子其实从标签数量就可以判断两个图是非同构图了，这里只是以此举个例子。）：

• a：给出两个标签 Label 的图 $G,G^{{}^{\prime }}$；
• b：考虑节点邻域的标签，并对此排序。（4,1135 表示当前节点标签为 4，其领域节点标签排序后为 1135）；
• c：对标签进行压缩映射；
• d：得到新标签；
• e：迭代 1 轮后，利用计数函数分别得到两张图的计数特征，得到图特征向量后便可计算图之间的相似性了。

直观上来看，WL-test 第 k 次迭代时节点的标号表示的是结点高度为 k 的子树结构：

以节点 1 为例，右图是节点 1 迭代两次的子树。因此 WL-test 所考虑的图特征本质上是图中以不同节点为根的子树的计数。

给出伪代码：

分别为：聚合邻居节点标签；多重集排序；标签压缩；更新标签。

公式表示为：
a v k = f ( { h u k − 1 : u ∈ N ( v ) } ) h v k = H a s h ( h v k − 1 , a v k ) a^{k}_v = f(\{h^{k-1}_u : u \in N(v)\}) \\ h^{k}_v = \mathbf{Hash} (h^{k-1}_v, a^{k}_v) \\ avk​=f({ huk−1​:u∈N(v)})hvk​=Hash(hvk−1​,avk​)
看到这大家是不是想到了什么？是不是和 GCN、GraphSAGE 等 GNN 网络的公式差不多？都是分为两步：聚合和结合：
a v k = A G G R E G A T E k ( {