【GNN】第八章 基于GIN的图表征学习

本文参考自datawhale2021.6学习：图神经网络

【GNN】第一章 图论基础

【GNN】第二章 PyG中的图与图数据集

【GNN】第三章 消息传递范式与PyG的MessagePassing基类

【GNN】第四章 节点表征学习与节点分类任务（理论+调包实操）

【GNN】第五章 构造数据完全存于内存的数据集类InMemoryDataset

【GNN】第六章 边预测任务

前言

• 图表征学习要求根据节点属性、边和边的属性（如果有的话）生成一个向量作为图的表征，基于图表征我们可以做图的预测
• 基于图同构网络（Graph Isomorphism Network, GIN）的图表征网络是当前最经典的图表征学习网络

在论文《How Powerful are Graph Neural Networks?》 中：

• 首先证明了 WL-test 是目前所有 GNN 的性能上界，
• 并通过分析目前 GNN 出现的问题提出了构建有效的 GNN 的方法：使用单射函数
• 同时也利用 MLP 拟合单射函数设计出一个新的架构模型 GIN，并通过实验证明 GIN 的性能逼近 WL-test

1 WL-test

目前解决图同构问题最有效的算法

1.1 同构图 Graph Isomorphism

• 两图的边和顶点数量相同，且边的连接性相同
• 也可以认为一图的点是由另一图的点映射得到
• 计算图同构可以度量图的相似度（比如实际应用中具有相似结构的分子可能具备相似的功能特性）
  
  

1.2 多重集 Multiset

一组可能重复的元素集合。例如：{1,1,2,3}就是一个多重集合

1.3 1-dimensional WL-test 及图相似度量

• 通过计算图特征向量来衡量图相似度。
• WL 算法可以是 K-维的，K-维 WL 算法在计算图同构问题时会考虑顶点的 k 元组。如果只考虑顶点的自身特征（如标签、颜色等），那么就是 1-维 WL 算法
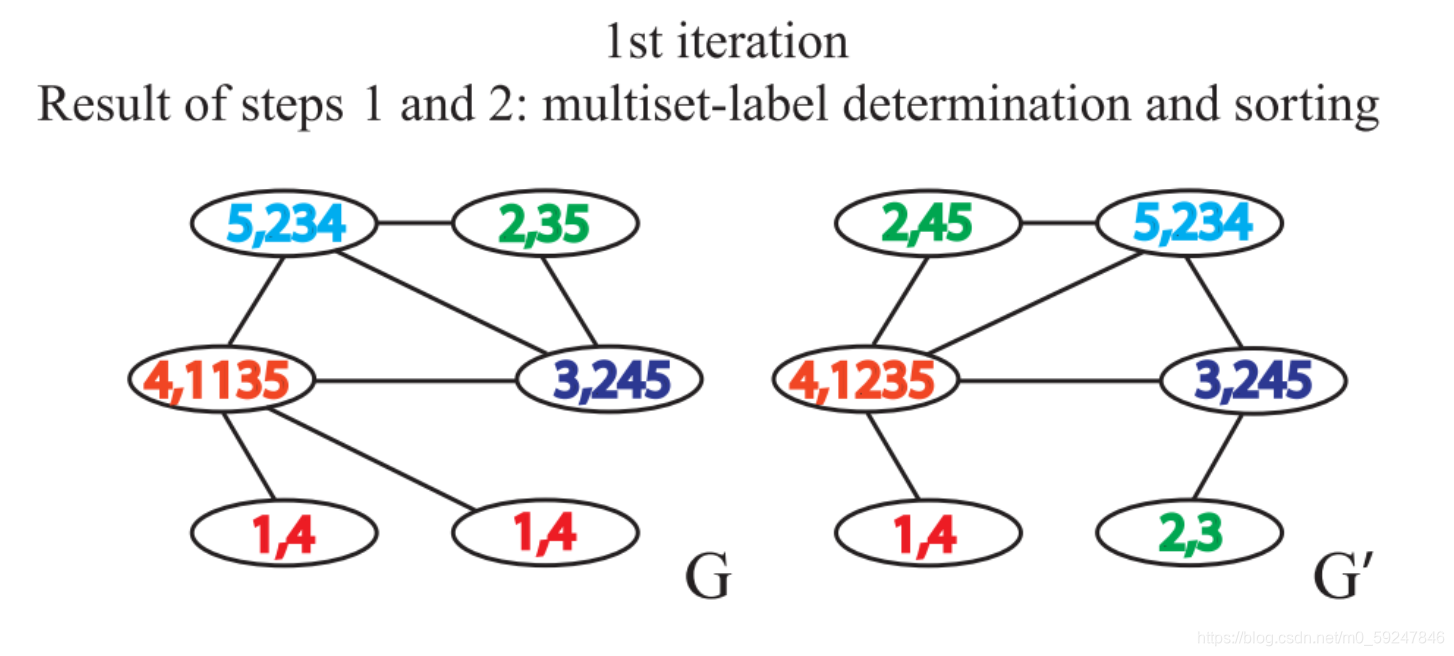
• 举例说明：一次迭代

1. 给定两个图$G$和$G^{\prime }$，每个节点拥有标签（实际中，一些图没有节点标签，我们可以以节点的度作为标签）
   

2.3. 考虑节点邻域的标签，并对此排序。逗号前是当前标签
排序的原因在于要保证单射性，即保证输出的结果不因邻接节点的顺序改变而改变

4. 对标签进行压缩映射

5. 得到新的标签

6. 计算图特征向量：迭代 1 轮后，利用计数函数分别得到两张图的计数特征，得到图特征向量后便可计算图之间的相似性了

• 当出现两个图相同节点标签的出现次数不一致时，即可判断两个图不相似
• 如果上述的步骤重复一定的次数后，没有发现有相同节点标签的出现次数不一致的情况，那么我们无法判断两个图是否同构

1.4 WL子树

• 在WL Test的第$k$次迭代中，一个节点的标签代表了：以该节点为根的高度为$k$的子树结构
• 当两个节点的$h$层的标签一样时，表示：分别以这两个节点为根节点的WL子树是一致的
• 举例：右图是节点1迭代两次的子树
  

1.5 WL-test的公式表示

• WL-test分为四步：聚合邻接节点标签、多重集排序、标签压缩、更新标签
• 公式：
  a v k = f ( { h u k − 1 : u ∈ N ( v ) } ) h v k = Hash ⁡ ( h v k − 1 , a v k ) a^{k}_v = f\left(\{ h^{k-1}_u:u\in N(v) \} \right) \\ h^{k}_{v} =\operatorname{Hash}\left(h_v^{k-1}, a_v^k\right) avk​=f({ huk−1​:u∈N(v)})hvk​=Hash(hvk−1​,avk​)
• 由公式发现，WL-test和GNN一样，学习节点表征分为两步：聚合和结合

2 GIN

2.1 单射的聚合方案

• 直观来说，一个好的 GNN 算法仅仅会在两个节点具有相同子树结构时才会将其映射到同一位置
• 由于子树结构是通过节点邻域递归定义的，所以我们可以将分析简化为这样一个问题：GNN 是否会映射两个邻域（即multiset）到相同的 Representation
• 一个好的 GNN 永远不会将两个不同领域映射得到相同的Representation。即，聚合模式必须是单射
• 因此，我们可以将 GNN 的聚合方案抽象为一类神经网络可以表示的多重集函数，并分析其是否是单射。

2.2 WL-test是GNN的上界

• 引理：
  • 对于两个非同构图$G_1$ 和 G 2 G_2 G