区别:
对偶上升:梯度上升的步长是针对每一次迭代都不固定。
增广拉格朗日方法:不过梯度上升的步长改成了固定的参数,而且罚项的系数也和这个步长有关。(一般取1)
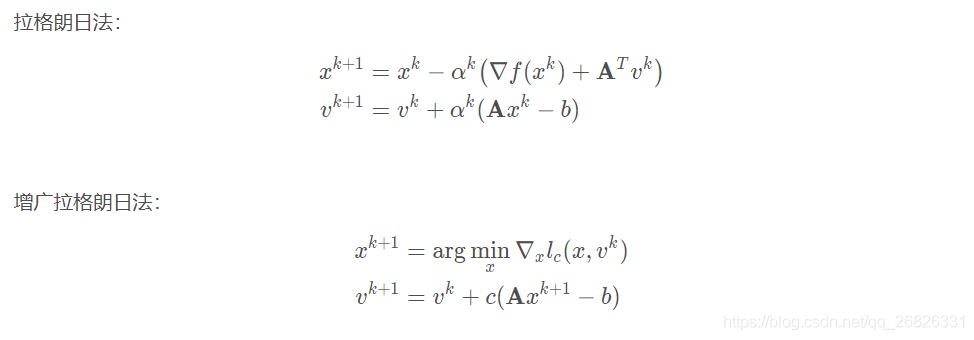
增广拉格朗日的鲁棒性更好,容易收敛。较为适合等式约束,对于不等式约束需要对问题进行变形,得到中间变量,然后对中间变量讨论求解。
类似于增广拉格朗日的方法:交替方向乘子法(ADMM)
 本文对比了对偶上升方法与增广拉格朗日方法在优化问题中的应用。对偶上升采用变化的步长,而增广拉格朗日使用固定步长,并具有更好的鲁棒性和收敛性,尤其适用于等式约束问题。文章还提到了类似方法——交替方向乘子法(ADMM)。
本文对比了对偶上升方法与增广拉格朗日方法在优化问题中的应用。对偶上升采用变化的步长,而增广拉格朗日使用固定步长,并具有更好的鲁棒性和收敛性,尤其适用于等式约束问题。文章还提到了类似方法——交替方向乘子法(ADMM)。
区别:
对偶上升:梯度上升的步长是针对每一次迭代都不固定。
增广拉格朗日方法:不过梯度上升的步长改成了固定的参数,而且罚项的系数也和这个步长有关。(一般取1)
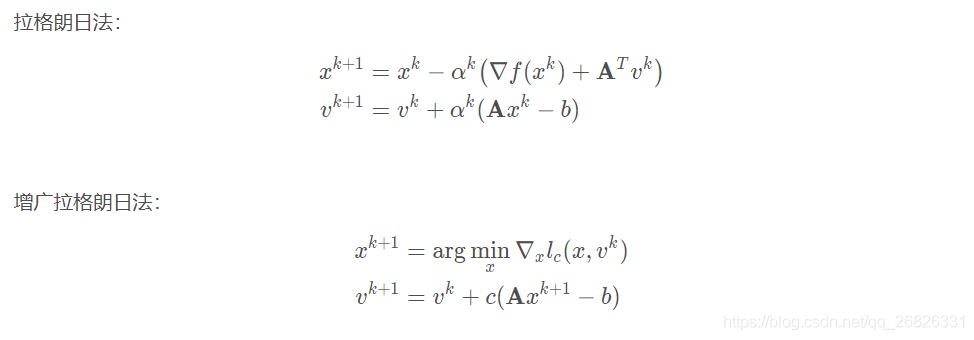
增广拉格朗日的鲁棒性更好,容易收敛。较为适合等式约束,对于不等式约束需要对问题进行变形,得到中间变量,然后对中间变量讨论求解。
类似于增广拉格朗日的方法:交替方向乘子法(ADMM)
 2万+
2万+
 4614
4614
 4763
4763

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


