全概率公式: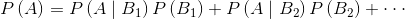
贝叶斯公式: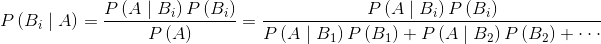
例题:
两个地区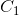 和
和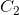 的人口比例是
的人口比例是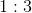 ,已知
,已知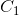 地区患某病的概率是
地区患某病的概率是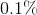 ,
,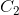 地区是
地区是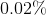 。现有一位该病患者,来自
。现有一位该病患者,来自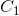 地区的概率是?
地区的概率是?
解1:根据贝叶斯公式
设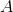 表示“一个人是该病患者”。
表示“一个人是该病患者”。
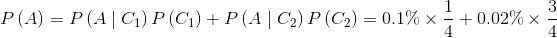 ,
,
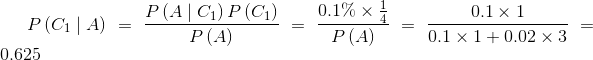 。
。
解2:根据比例关系
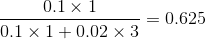 。
。
全概率公式: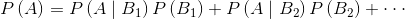
贝叶斯公式: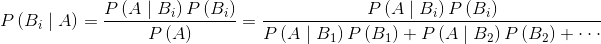
例题:
两个地区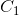 和
和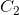 的人口比例是
的人口比例是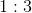 ,已知
,已知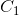 地区患某病的概率是
地区患某病的概率是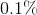 ,
,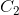 地区是
地区是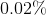 。现有一位该病患者,来自
。现有一位该病患者,来自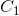 地区的概率是?
地区的概率是?
解1:根据贝叶斯公式
设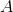 表示“一个人是该病患者”。
表示“一个人是该病患者”。
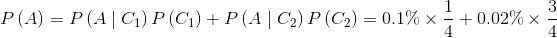 ,
,
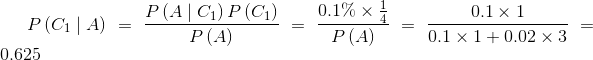 。
。
解2:根据比例关系
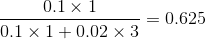 。
。
 2311
2311

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


