第十七课 : 旋转

最新推荐文章于 2025-07-17 18:24:49 发布

KenneySH

最新推荐文章于 2025-07-17 18:24:49 发布

阅读量2.8k

点赞数 2

分类专栏： OpenGL

OpenGL 专栏收录该内容

30 篇文章

订阅专栏

翻译自：http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-17-quaternions/

Tutorial 17 : Rotations

第十七课 : 旋转

This tutorial goes a bit outside the scope of OpenGL, but nevertheless tackles a very common problem: how to represent rotations ?

这篇教程有点超出了OpenGL的范畴，它讲解了一个常用的问题：如何旋转？

In Tutorial 3 - Matrices, we learnt that matrices are able to rotate a point around a specific axis. While matrices are a neat way to transform vertices, handling matrices is difficult: for instance, getting the rotation axis from the final matrix is quite tricky.

在第三课-矩阵中，我们学习了如何使用矩阵让点围绕特定轴进行旋转。虽然使用矩阵对点进行变换十分的简洁，但是处理矩阵却相对比较复杂：比如从最终的矩阵中得到旋转轴。

We will present the two most common ways to represent rotation: Euler angles and Quaternions. Most importantly, we will explain why you should probably use Quaternions.

我们将会使用两种常用的方法来表达旋转：欧拉角与四元数。最重要的是，我们会解释你为什么需要合理使用四元数。

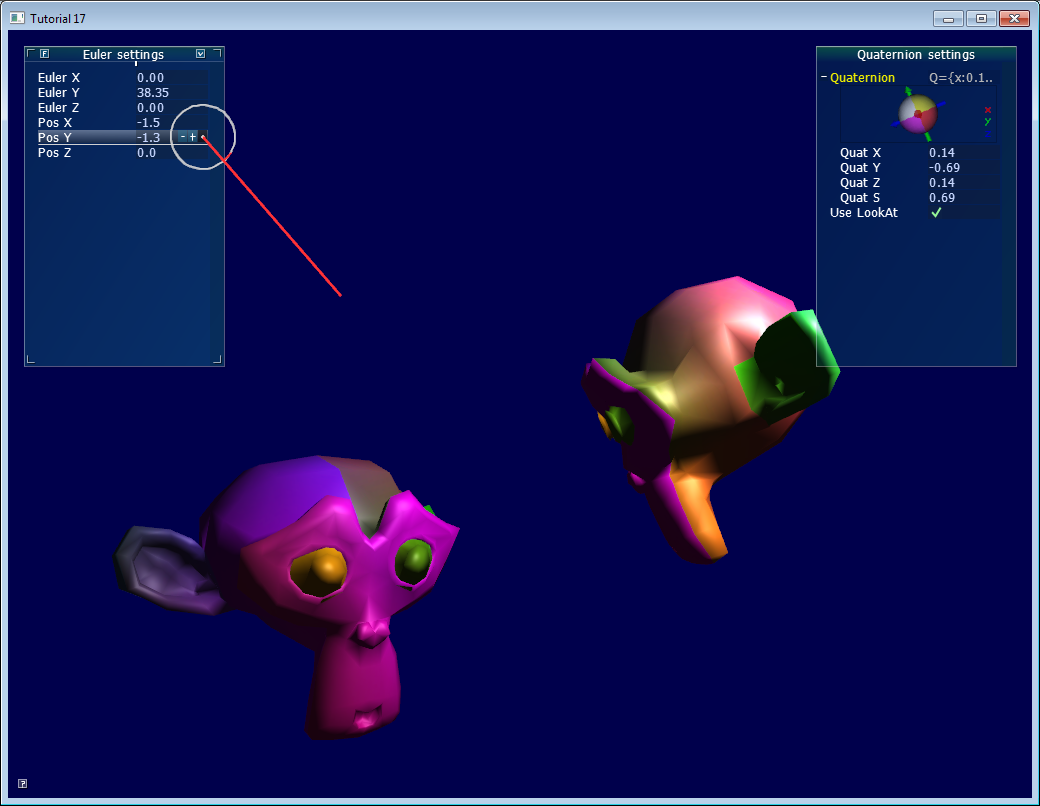
Foreword: rotation VS orientation

引言：旋转与方向

While reading articles on rotations, you might get confused because of the vocabulary. In this tutorial:

An orientation is a state: “the object’s orientation is…”
A rotation is an operation: “Apply this rotation to the object”

That is, when you apply a rotation, you change the orientation. Both can be represented with the same tools, which leads to the confusion. Now, let’s get started…

当在读旋转这篇教程时，你可能会被这样的词汇所困扰。在这篇教程中：

方向是这种状态：“对象的方向是...”

旋转是一种操作：“对这个对象应用旋转”

当你应用旋转时，你改变了方向。由于两者的表述方式类似，所以可能会导致混淆。现在让我们正式开始...

Euler Angles

欧拉角

Euler angles are the easiest way to think of an orientation. You basically store three rotations around the X, Y and Z axes. It’s a very simple concept to grasp. You can use a vec3 to store it:

欧拉角是用来表达方向的最简单的方式。你可以存储XYZ轴的三个旋转分量，这点很容易理解。你可以使用一个vec3来保存它：

1 vec3 EulerAngles( RotationAroundXInRadians, RotationAroundYInRadians, RotationAroundZInRadians);

These 3 rotations are then applied successively, usually in this order: first Y, then Z, then X (but not necessarily). Using a different order yields different results.

这三个旋转分量使用起来很方便，通常按照YZX轴的顺序进行变换(不是必须的)。使用不同的顺序最终得出的结果是不同的。

One simple use of Euler angles is setting a character’s orientation. Usually game characters do not rotate on X and Z, only on the vertical axis. Therefore, it’s easier to write, understand and maintain “float direction;” than 3 different orientations.

欧拉角的一个简单的应用是角色的方向。通常游戏角色不会旋转X和Z轴，只会旋转垂直轴。因此，相对于3个不同方向，角色朝向这个概念会很容易编写，理解和维护。

Another good use of Euler angles is an FPS camera: you have one angle for the heading (Y), and one for up/down (X). Seecommon/controls.cpp for an example.

欧拉角另一个很好的应用是FPS相机：你有一个角度用于左右旋转(Y轴)，一个角度用于上下旋转(X轴)。参见common/controls.cpp。

However, when things get more complex, Euler angle will be hard to work with. For instance :

然而，当索要处理更复杂的事情时，欧拉角使用起来就会比较麻烦，例如：

Interpolating smoothly between 2 orientations is hard. Naively interpolating the X,Y and Z angles will be ugly.
Applying several rotations is complicated and unprecise: you have to compute the final rotation matrix, and guess the Euler angles from this matrix
A well-known problem, the “Gimbal Lock”, will sometimes block your rotations, and other singularities which will flip your model upside-down.
Different angles make the same rotation ( -180° and 180°, for instance )
It’s a mess - as said above, usually the right order is YZX, but if you also use a library with a different order, you’ll be in trouble.
Some operations are complicated: for instance, rotation of N degrees around a specific axis.
在两个方向之间平滑的插值很困难。简单的对XYZ角度进行插值得出的结果很难看。
执行多个旋转的时候很复杂并且不精确：你需要计算最终的旋转矩阵，然后猜测这个矩阵中的欧拉角
一个总所周知的问题，万向节死锁，有时会妨碍你的旋转，在一些奇异点会导致你的模型颠倒
不同的角度导致相同的旋转(-180度与180度)
通常使用的旋转顺序是YZX，但如果你使用了一个不同旋转顺序的库，你就会遇到一些麻烦，它会使你的旋转乱的一团糟。
有些操作很复杂：例如，绕任意轴旋转一定角度。

Quaternions are a tool to represent rotations, which solves these problems.

四元数是表达旋转的工具，它解决了这些问题。

Quaternions

四元数

A quaternion is a set of 4 numbers, [x y z w], which represents rotations the following way:

四元数由4个数字[x y z w]来表达：

1 // RotationAngle is in radians
2 x = RotationAxis.x * sin(RotationAngle / 2)
3 y = RotationAxis.y * sin(RotationAngle / 2)
4 z = RotationAxis.z * sin(RotationAngle / 2)
5 w = cos(RotationAngle / 2)

RotationAxis is, as its name implies, the axis around which you want to make your rotation.

RotationAxis就像名字所描述的一样，是你的旋转轴。

RotationAngle is the angle of rotation around this axis.

Rotation是你围绕旋转轴旋转的角度。

So essentially quaternions store a rotation axis and a rotation angle, in a way that makes combining rotations easy.

所以四元数本质上存储的是一个旋转轴以及一个旋转角度，使得结合旋转更容易。

Reading quaternions

读四元数

This format is definitely less intuitive than Euler angles, but it’s still readable: the xyz components match roughly the rotation axis, and w is the acos of the rotation angle (divided by 2). For instance, imagine that you see the following values in the debugger: [ 0.7 0 0 0.7 ]. x=0.7, it’s bigger than y and z, so you know it’s mostly a rotation around the X axis; and 2*acos(0.7) = 1.59 radians, so it’s a rotation of 90°.

Similarly, [0 0 0 1] (w=1) means that angle = 2*acos(1) = 0, so this is a unit quaternion, which makes no rotation at all.

四元数的结构相对于欧拉角而言不那么的直观，但它仍然是可读的：xyz轴分量大致表示了旋转轴，w分量是旋转角的除以2的cos值（这里是个人的理解w=cos(角度/2)，前面的公式也有提到）。例如，你再调试器里看到[0.7 0 0 0.7]这样一组数字，其中x=0.7，它比y和z要大，所以你知道它可能是绕x轴进行旋转。然后2*acos(0.7)=1.59，所以它旋转90度。

类似的，[0 0 0 1](w=1)意味着旋转角=2*acos(1)=0，所以它是一个单位四元数，表示没有旋转。

Basic operations

基础操作

Knowing the math behind the quaternions is rarely useful: the representation is so unintuitive that you usually only rely on utility functions which do the math for you. If you’re interested, see the math books in the Useful Tools & Links page.

知道四元数背后的数学知识是非常有用的：你通常会依赖使用工具函数来为你进行计算它们使用起来是那么的直观，如果有兴趣的话可以看下Useful Tools&Links中的数学部分。

How do I create a quaternion in C++ ?

如何在C++中创建四元数？

 1 // Don't forget to #include <glm/gtc/quaternion.hpp> and <glm/gtx/quaternion.hpp>
 2 
 3 // Creates an identity quaternion (no rotation)
 4 quat MyQuaternion;
 5 
 6 // Direct specification of the 4 components
 7 // You almost never use this directly
 8 MyQuaternion = quat(w,x,y,z); 
 9 
10 // Conversion from Euler angles (in radians) to Quaternion
11 vec3 EulerAngles(90, 45, 0);
12 MyQuaternion = quat(EulerAngles);
13 
14 // Conversion from axis-angle
15 // In GLM the angle must be in degrees here, so convert it.
16 MyQuaternion = gtx::quaternion::angleAxis(degrees(RotationAngle), RotationAxis);

How do I create a quaternion in GLSL ?

如何在GLSL中创建四元数？

You don’t. Convert your quaternion to a rotation matrix, and use it in the Model Matrix. Your vertices will be rotated as usual, with the MVP matrix.

In some cases, you might actually want to use quaternions in GLSL, for instance if you do skeletal animation on the GPU. There is no quaternion type in GLSL, but you can pack one in a vec4, and do the math yourself in the shader.

将你四元数转换为旋转矩阵，然后在模型矩阵中使用。使用MVP矩阵的话，你的顶点会和往常一样进行旋转。

在某些情况下，你可能真的希望在GLSL中使用四元数，例如在GPU中计算骨骼动画。在GLSL中没有四元数类型，但是你可以自己组织一个vec4类型，然后在shader中自己计算。

How do I convert a quaternion to a matrix ?

如何将四元数转换成矩阵？

1 mat4 RotationMatrix = quaternion::toMat4(quaternion);

You can now use it to build your Model matrix as usual:

你现在可以和往常一样构建你的模型矩阵：

1 mat4 RotationMatrix = quaternion::toMat4(quaternion);
2 ...
3 mat4 ModelMatrix = TranslationMatrix * RotationMatrix * ScaleMatrix;
4 // You can now use ModelMatrix to build the MVP matrix

So, which one should I choose ?

如何抉择？

Choosing between Euler angles and quaternions is tricky. Euler angles are intuitive for artists, so if you write some 3D editor, use them. But quaternions are handy for programmers, and faster too, so you should use them in a 3D engine core.

在欧拉角与四元数之间进行抉择是微妙的。在使用3D编辑器时，欧拉角对于美术而言更加直观。但在3D核心引擎中，程序员处理四元数更加的快捷。

The general consensus is exactly that: use quaternions internally, and expose Euler angles whenever you have some kind of user interface.

通常共识是：在内部使用四元数，在用户接口中使用四元数。

You will be able to handle all you will need (or at least, it will be easier), and you can still use Euler angles for entities that require it ( as said above: the camera, humanoids, and that’s pretty much it) with a simple conversion.

你可以在简单的应用中使用欧拉角，比如之前提到的相机，角色等。

Other resources

其他资源

The books on Useful Tools & Links !
As old as it can be, Game Programming Gems 1 has several awesome articles on quaternions. You can probably find them online too.
A GDC presentation on rotations
The Game Programing Wiki’s Quaternion tutorial
Ogre3D’s FAQ on quaternions. Most of the 2nd part is ogre-specific, though.
Ogre3D’s Vector3D.h and Quaternion.cpp

Cheat-sheet

小抄

How do I know if two quaternions are similar ?

如何判断两个四元数是否相似？

When using vector, the dot product gives the cosine of the angle between these vectors. If this value is 1, then the vectors are in the same direction.

当使用向量时候，点积代表两个向量之间夹角的cos值。如果计算结果为1，那么这两个向量是同向的。

With quaternions, it’s exactly the same:

对于四元数而言也一样。

1 float matching = quaternion::dot(q1, q2);
2 if ( abs(matching-1.0) < 0.001 ){
3     // q1 and q2 are similar
4 }

You can also get the angle between q1 and q2 by taking the acos() of this dot product.

How do I apply a rotation to a point ?

如何使用四元数旋转一个点？

You can do the following:

你可以按照如下步骤操作：

1 rotated_point = orientation_quaternion *  point;

… but if you want to compute your Model Matrix, you should probably convert it to a matrix instead.

如果你想计算你的模型矩阵，你需要转换成一个矩阵。

Note that the center of rotation is always the origin. If you want to rotate around another point:

注意旋转的中心永远是原点。如果你想绕某点进行旋转，需要将该点变换到原点进行旋转，旋转完后再变换回来。

1 rotated_point = origin + (orientation_quaternion * (point-origin));

How do I interpolate between 2 quaternions ?

如何在两个四元数之间进行插值？

This is called a SLERP: Spherical Linear intERPolation. With GLM, you can do this with mix:

SLERP：球面线性插值。在GLM中你可以这样混合：

1 glm::quat interpolatedquat = quaternion::mix(quat1, quat2, 0.5f); // or whatever factor

How do I cumulate 2 rotations ?

如何对2个旋转进行相加？

Simple ! Just multiply the two quaternions together. The order is the same as for matrices, i.e. reverse:

简单！将两个四元数相乘。和矩阵的指令是一样的，反之亦然。

1 quat combined_rotation = second_rotation * first_rotation;

How do I find the rotation between 2 vectors ?

如何计算两个向量之间的旋转？

(in other words: the quaternion needed to rotate v1 so that it matches v2)

换句话说，使用四元数旋转v1到v2

The basic idea is straightforward:

基本概念是明确的：

The angle between the vectors is simple to find: the dot product gives its cosine.
The needed axis is also simple to find: it’s the cross product of the two vectors.
两个向量之间的夹角很容易计算：计算两个亮点的点积得到余弦值。
所需要的旋转轴也可以简单计算得到：它是两个向量的叉积。

The following algorithm does exactly this, but also handles a number of special cases:

以下算法实现了上述算法，并处理了一些异常情况：

 1 quat RotationBetweenVectors(vec3 start, vec3 dest){
 2 	start = normalize(start);
 3 	dest = normalize(dest);
 4 
 5 	float cosTheta = dot(start, dest);
 6 	vec3 rotationAxis;
 7 
 8 	if (cosTheta < -1 + 0.001f){
 9 		// special case when vectors in opposite directions:
10 		// there is no "ideal" rotation axis
11 		// So guess one; any will do as long as it's perpendicular to start
12 		rotationAxis = cross(vec3(0.0f, 0.0f, 1.0f), start);
13 		if (gtx::norm::length2(rotationAxis) < 0.01 ) // bad luck, they were parallel, try again!
14 			rotationAxis = cross(vec3(1.0f, 0.0f, 0.0f), start);
15 
16 		rotationAxis = normalize(rotationAxis);
17 		return gtx::quaternion::angleAxis(180.0f, rotationAxis);
18 	}
19 
20 	rotationAxis = cross(start, dest);
21 
22 	float s = sqrt( (1+cosTheta)*2 );
23 	float invs = 1 / s;
24 
25 	return quat(
26 		s * 0.5f, 
27 		rotationAxis.x * invs,
28 		rotationAxis.y * invs,
29 		rotationAxis.z * invs
30 	);
31 
32 }

(You can find this function in common/quaternion_utils.cpp)

I need an equivalent of gluLookAt. How do I orient an object towards a point ?

我需要一个类似于gluLookAt的函数。我如何将一个对象指向一个点？

Use RotationBetweenVectors !

使用RotationBetweenVectors

1 // Find the rotation between the front of the object (that we assume towards +Z,
2 // but this depends on your model) and the desired direction
3 quat rot1 = RotationBetweenVectors(vec3(0.0f, 0.0f, 1.0f), direction);

Now, you might also want to force your object to be upright:

1 // Recompute desiredUp so that it's perpendicular to the direction
2 // You can skip that part if you really want to force desiredUp
3 vec3 right = cross(direction, desiredUp);
4 desiredUp = cross(right, direction);
5 
6 // Because of the 1rst rotation, the up is probably completely screwed up.
7 // Find the rotation between the "up" of the rotated object, and the desired up
8 vec3 newUp = rot1 * vec3(0.0f, 1.0f, 0.0f);
9 quat rot2 = RotationBetweenVectors(newUp, desiredUp);

Now, combine them:

1 quat targetOrientation = rot2 * rot1; // remember, in reverse order.

Beware, “direction” is, well, a direction, not the target position ! But you can compute the position simply: targetPos - currentPos.

Once you have this target orientation, you will probably want to interpolate between startOrientation and targetOrientation.

(You can find this function in common/quaternion_utils.cpp)

注意方向就是方向，它不是一个目标的位置！你可以简单的用:targetPos-currentPos来计算得到。

一旦你得到了这个目标方向，你可能会需要在开始方向和目标方向之间进行插值。

How do I use LookAt, but limit the rotation at a certain speed ?

如何使用LookAt，并且将旋转限定在一定的速度范围内？

The basic idea is to do a SLERP ( = use glm::mix ), but play with the interpolation value so that the angle is not bigger than the desired value:

基本概念是使用球面线性插值(使用glm::mix)。使用插值计算所得到的值以便发生角度超出预期的情况：

1 float mixFactor = maxAllowedAngle / angleBetweenQuaternions;
2 quat result = glm::gtc::quaternion::mix(q1, q2, mixFactor);

Here is a more complete implementation, which deals with many special cases. Note that it doesn’t use mix() directly as an optimization.

以下是一个更加完整的实现，它处理了很多特殊情况。注意它没有直接使用mix函数来做优化。

 1 quat RotateTowards(quat q1, quat q2, float maxAngle){
 2 
 3 	if( maxAngle < 0.001f ){
 4 		// No rotation allowed. Prevent dividing by 0 later.
 5 		return q1;
 6 	}
 7 
 8 	float cosTheta = dot(q1, q2);
 9 
10 	// q1 and q2 are already equal.
11 	// Force q2 just to be sure
12 	if(cosTheta > 0.9999f){
13 		return q2;
14 	}
15 
16 	// Avoid taking the long path around the sphere
17 	if (cosTheta < 0){
18 	    q1 = q1*-1.0f;
19 	    cosTheta *= -1.0f;
20 	}
21 
22 	float angle = acos(cosTheta);
23 
24 	// If there is only a 2&deg; difference, and we are allowed 5&deg;,
25 	// then we arrived.
26 	if (angle < maxAngle){
27 		return q2;
28 	}
29 
30 	float fT = maxAngle / angle;
31 	angle = maxAngle;
32 
33 	quat res = (sin((1.0f - fT) * angle) * q1 + sin(fT * angle) * q2) / sin(angle);
34 	res = normalize(res);
35 	return res;
36 
37 }

You can use it like that:

你可以这样使用上面的函数。

1 CurrentOrientation = RotateTowards(CurrentOrientation, TargetOrientation, 3.14f * deltaTime );

(You can find this function in common/quaternion_utils.cpp)

How do I…

If you can’t figure it out, drop us an email, and we’ll add it to the list !