算法题（Math）---持续更新

最新推荐文章于 2024-08-12 10:44:50 发布

CLthinking

最新推荐文章于 2024-08-12 10:44:50 发布

阅读量184

点赞数

CC 4.0 BY-SA版权

分类专栏：算法题

本文链接：https://blog.youkuaiyun.com/qq_22158743/article/details/88812728

算法题专栏收录该内容

14 篇文章

订阅专栏

博客涵盖了三个算法问题：1. 找到数列中第n位的数字，涉及数字长度计算和定位。2. 整数替换，讨论如何通过变换次数最少地将正整数n替换为1，提出了两种解法。3. 计算无重复数字的个数，与高中排列组合知识相关。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、找第n位数字。

无限数列1,2,3,4,5,6,7,8,9,10,11,12......。第一位是1，第五位是5，第十位是1（10的第首位），第十一位是0（10的末位），第十二位是1（11的首位）........

三步：1、找到第n位所在数字的长度。2，找到第n位所在的具体数字。3，返回第n位。

    public int findNthDigit(int n) {
        int len = 1;
        long count = 9;
        int start = 1;
        while(n > len * count) {
            n -= len * count;
            len++;
            count *= 10;
            start *= 10;
        }
        start += (n - 1) / len;
        String s = Integer.toString(start);
        return Character.getNumericValue(s.charAt((n - 1) % len));
    }

2、整数替换。

给定一个正整数n，可以对它进行两种变换：1、如果是偶数，替换该数为n/2。2、如果是奇数，可以替换为n + 1或者n - 1。求最小的次数将n替换为1。

解法1：直观的解法

class Solution {
    public int integerReplacement(int n) {
        return help(n ,0);
    }
    private int help(long n, int count) {
        if(n == 1) return count;
        if((n & 1) == 0 ) {
            return help(n >> 1, count + 1);
        } else {
            return Math.min(help(n + 1, count + 1), help(n - 1, count + 1));
        }
    }
}

解法2：当数为奇数时，我们通过+1，或者-1应该得到更多的0才能使次数最小：例如 0111我们应该加1：

1111->10000->1000->100->10->1。如果减1的话：1111->1110->111->110->11->10->1。因此当末尾两位2进制为都为1时我们应该加1（只有3是例外。11->100->10->1 11->10->1）因为这种情况下我们加1会得到更多的0，其余的情况减1。

class Solution {
    public int integerReplacement(long n) {
        int res = 0;
        while(n != 1) {
            if((n & 1) == 0) {
                n >>= 1;
            } else if((n & 2) == 0 || n == 3) {
                n--;
            } else {
                n++;
            }
            res++;
        }
        return res;
    }
}

3、计算没有重复数字的个数

Given a non-negative integer n, count all numbers with unique digits, x, where 0 ≤ x < 10n.

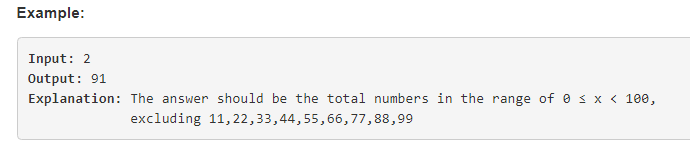
这道题就是高中学的排列组合的知识：

class Solution {
    public int countNumbersWithUniqueDigits(int n) {
        if(n == 0) return 1;
        if(n > 10) return 0;
        int res = 10, cur = 9;
        for(int i = 2; i <= n; ++i) {
            cur = cur * (11 - i);
            res += cur;
        }
        return res;
    }
}