数位dp-HDU - 4352-LIS状态压缩

最新推荐文章于 2020-11-28 18:29:04 发布

H_ang

最新推荐文章于 2020-11-28 18:29:04 发布

阅读量172

点赞数 1

CC 4.0 BY-SA版权

分类专栏：数位dp

本文链接：https://blog.youkuaiyun.com/qq_21433411/article/details/95037128

数位dp 专栏收录该内容

6 篇文章

订阅专栏

本文介绍了一种解决区间内寻找特定长度最长递增子序列问题的方法，通过状态压缩和动态规划技术，在O(n*logn)的时间复杂度内求解。特别关注于数字0-9范围内的问题，利用二进制位表示状态，巧妙地处理前导0的影响。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4352
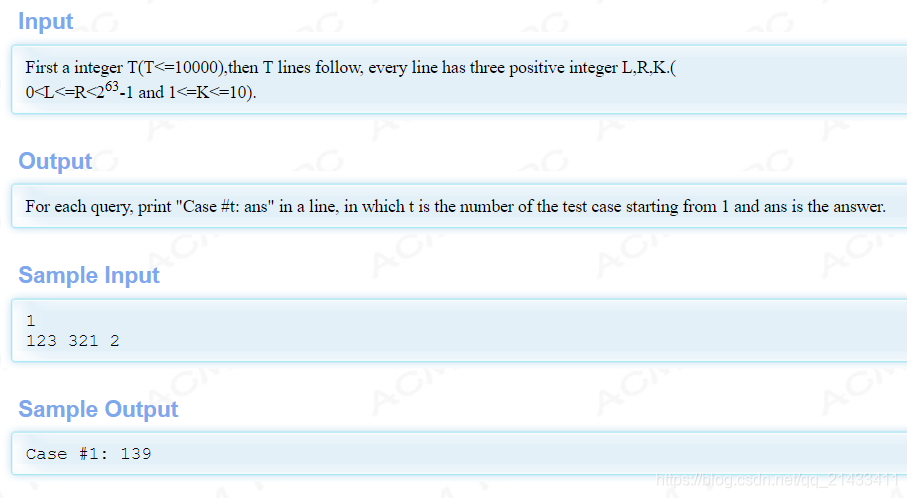
题目大意：题意：介绍了电子科大的一个传奇学姐，最后几句话才是题意，这题意思就是给你一个LL范围内的区间[L, R]，问你在这个区间内最长递增子序列长度恰为K的数有多少个。
在这里插入图片描述

在dp过程中，我们要维护LIS。而且数字只有0-9,如果你知道怎么在O(n * logn)的时间复杂度维护LIS，那么就好办了。但是这个方法用维护一个栈，每次替换栈中第一个大于当前值的数。但是我们怎么把一个大小最大为10的栈表示为状态。就是状态压缩：用一个int来表示栈0000000000。这表示一个空栈。

举例来说：如果sta按照数字13425来更新。
首先遇到1，变成 0100000000 （或者0000000010，其实这是完全一样的，只要保证不同状态的sta不一样就行了）
然后遇到3，很明显，之前没有比3更大的数字，然后变成0101000000

遇到4，sta变成0101100000

在这里打断一下，不能看出，sta中1的个数，就是LIS的长度。

然后遇到2，这时大于等于2的有一个3.于是把3的二进制1交给2，sta变成0110100000 实现替换。遇到4，sta变成0101100000

所以：sta中1的个数，就是LIS的长度。

当然要判断前导0，例如：1 10 2，如果没有判断前导0，那么pos=1时，当前数为0，栈变1000000000，再枚举pos=0时，那么1 2 3 4 5 6 7 8 9都满足条件了。所以必须考虑前导0的影响。

#include <bits/stdc++.h>
#define LL long long
using namespace std;
LL a[20];
LL dp[20][1024][15];

LL Size(LL x)//二进制0的个数
{
    LL ans=0;
    while(x)
    {
        ans+=(x&1);
        x>>=1;
    }
    return ans;
}

LL Lis(LL st, LL k)//维护LIS
{
    for(LL i=k;i<10;i++)//第一个>k的数
    {
        if(st&(1<<i))
        {
            return (st^(1<<i))|(1<<k);
        }
    }

    return st|(1<<k);
}

LL dfs(LL pos, LL st, LL Lead, LL mt, LL k)
{
    if(pos==-1)
    {
        if(Size(st)==k)//LIS==k
        {
            return 1;
        }
        else
        {
            return 0;
        }
    }
    if(!Lead&&!mt&&dp[pos][st][k]!=-1)
    {
        return dp[pos][st][k];
    }

    LL Len=mt?a[pos]:9;
    LL ans=0;
    for(LL i=0;i<=Len;i++)
    {
        ans+=dfs(pos-1, (i==0&&Lead)?st:Lis(st, i), Lead&&(i==0), mt&&(i==a[pos]), k);//考虑前导0
    }

    if(!mt&&!Lead)
    {
        dp[pos][st][k]=ans;
    }

    return ans;
}

LL slove(LL x, LL k)
{
    LL pos=0;
    while(x)
    {
        a[pos++]=x%10;
        x/=10;
    }
    return dfs(pos-1, 0, 1, 1, k);
}

int main()
{
    LL T, CUT=1;
    memset(dp, -1, sizeof(dp));
    scanf("%lld",&T);
    while(T--)
    {
        LL L, R, k;
        scanf("%lld%lld%lld",&L,&R,&k);
        printf("Case #%lld: %lld\n",CUT++, slove(R, k)-slove(L-1, k));
    }

    return 0;
}