概率专题迷宫任意门回到原点的期望

最新推荐文章于 2020-07-31 20:35:22 发布

原创最新推荐文章于 2020-07-31 20:35:22 发布 · 709 阅读

1 ·

CC 4.0 BY-SA版权

概率专栏收录该内容

15 篇文章

订阅专栏

博客给出题目链接，题目是在迷宫中有n扇门，每扇门有数字k，k为正走k分钟出去，k为负走 -k分钟回迷宫，各扇门概率相同，要求走出迷宫所需时间的期望值，还指出若全是负数则为inf。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：https://vjudge.net/contest/299639#problem/A
题目大意：
你在一个迷宫里,面前有n扇们,每个门有一个数字k;如果k为正数,则通过这扇门,走k分钟就能出去,如果为负数,则通过这扇门走-k的分钟回到迷宫;走每扇门概率一样.问走出迷宫所需时间的期望值;
首先如果全是负数肯定是inf;

然后我们假设我们走出去的期望时间是d;
那么拿第三个样例举例子; d = 1/3 * 3  + 1/3( 6 + d) + 1/3 (9 + d);
意思就是每扇门被选择的概率是1/3;
选第一扇门要花3分钟出去,选第二扇门要6 + d(花6分钟返回原地,在花期望d出去);

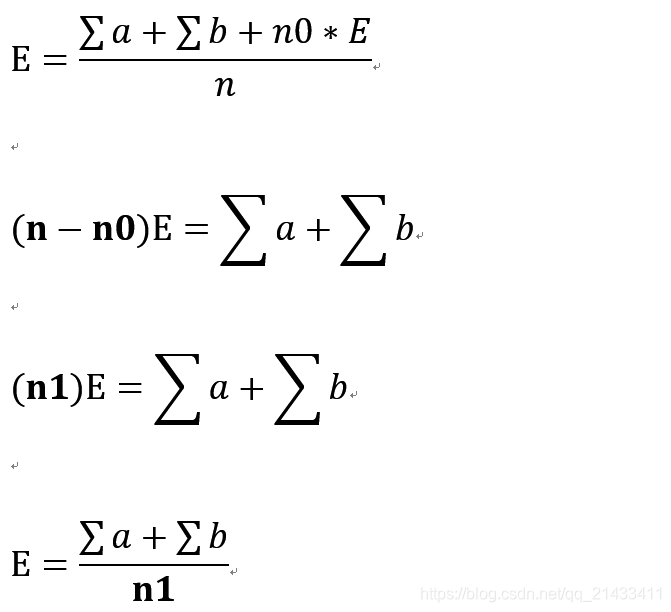
在这里插入图片描述

#include<bits/stdc++.h>
#define LL long long
using namespace std;

LL a[2000];
int main()
{
    int t, CUT=0;
    scanf("%d",&t);
    while(t--)
    {
        CUT++;
        LL n;
        scanf("%lld",&n);
        LL n0=0, n1=0, s0=0, s1=0;
        for(int i=0;i<n;i++)
        {
            scanf("%lld",&a[i]);
            if(a[i]>0)
            {
                s0+=a[i];
                n1++;
            }
            else
            {
                s1+=a[i];
                n0++;
            }
        }
        LL ans=s0-s1;
        cout<<"Case "<<CUT<<": ";
        if(s0==0)
        {
            cout<<"inf"<<endl;
        }
        else
        {
            cout<<ans/__gcd(ans, n1)<<'/'<<n0/__gcd(ans, n1)<<endl;
        }
    }

    return 0;
}