LeetCode-85. Maximal Rectangle [C++][Java]

目录

一、题目描述

二、解题思路

1. 动态规划+单调栈

【C++】

【Java】

2. 动态规划+双指针

【C++】

【Java】

---

LeetCode-85. Maximal Rectanglehttps://leetcode.com/problems/maximal-rectangle/description/

一、题目描述

Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

Example 1:

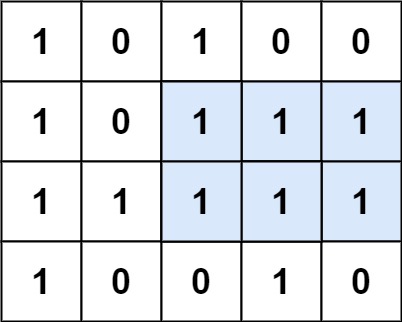
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 6
Explanation: The maximal rectangle is shown in the above picture.

Example 2:

Input: matrix = [["0"]]
Output: 0

Example 3:

Input: matrix = [["1"]]
Output: 1

Constraints:

• rows == matrix.length
• cols == matrix[i].length
• 1 <= row, cols <= 200
• matrix[i][j] is '0' or '1'.

二、解题思路

1. 动态规划+单调栈

• 时间复杂度为 O(mn)

• 空间复杂度为 O(n)

【C++】

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int m = matrix.size(), n = matrix[0].size(), res = 0;
        if (m == 0 || n == 0) {
            return res;
        }
        vector<int> height(n, 0);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                height[j] = matrix[i][j] == '1' ? height[j] + 1 : 0;
            }
            vector<int> left(n, -1), right(n, n); 
            stack<int> st;
            for (int j = 0; j < n; ++j) {
                while (!st.empty() && height[st.top()] >= height[j]) {
                    right[st.top()] = j;
                    st.pop();
                }
                if (!st.empty()) {
                    left[j] = st.top();
                }
                st.push(j);
            }
            for (int j = 0; j < n; ++j) {
                res = max(res, height[j] * (right[j] - left[j] - 1));
            }
        }
        return res;
    }
};

【Java】

public class Solution {
    public int maximalRectangle(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int m = matrix.length, n = matrix[0].length, res = 0;
        int[] height = new int[n];
        Arrays.fill(height, 0);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                height[j] = matrix[i][j] == '1' ? height[j] + 1 : 0;
            }
            int[] left = new int[n];
            int[] right = new int[n];
            Arrays.fill(left, -1);
            Arrays.fill(right, n);
            Stack<Integer> st = new Stack<>();
            for (int j = 0; j < n; j++) {
                while (!st.isEmpty() && height[st.peek()] >= height[j]) {
                    right[st.pop()] = j;
                }
                if (!st.isEmpty()) {
                    left[j] = st.peek();
                }
                st.push(j);
            }
            for (int j = 0; j < n; j++) {
                res = Math.max(res, height[j] * (right[j] - left[j] - 1));
            }
        }
        return res;
    }
}

2. 动态规划+双指针

• 时间复杂度为 O(mn)

• 空间复杂度为 O(n)

【C++】

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int m = matrix.size(), n = matrix[0].size(), res = 0;
        if(m == 0 || n == 0) {
            return res;
        }
        vector<int> left(n, 0), right(n, n), height(n, 0);
        int cur_left = 0, cur_right = n;
        for (int i = 0 ; i < m; ++i) {
            cur_left = 0;
            cur_right = n;
            for(int j = 0;  j < n; ++j) {
                if (matrix[i][j] == '0') {
                    height[j] = 0;
                    left[j] = 0;
                    cur_left = j + 1;
                } else {
                    height[j] += 1;
                    left[j] = max(left[j], cur_left);
                }
            }
            for (int j = n - 1; j >= 0; --j) {
                if (matrix[i][j] == '0') {
                    cur_right = j;
                    right[j] = n;
                } else {
                    right[j] = min(right[j], cur_right);
                    res = max(res, (right[j] - left[j]) * height[j]);
                }
            }
        }
        return res;
    }
};

【Java】

class Solution {
    public int maximalRectangle(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int m = matrix.length, n = matrix[0].length, res = 0;
        int[] left = new int[n];
        int[] right = new int[n];
        int[] height = new int[n];
        Arrays.fill(left, -1);
        Arrays.fill(right, n);
        Arrays.fill(height, 0);
        
        for (int i = 0; i < m; i++) {
            int curLeft = 0;
            int curRight = n;
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '0') {
                    height[j] = 0;
                    left[j] = 0;
                    curLeft = j + 1;
                } else {
                    height[j]++;
                    left[j] = Math.max(left[j], curLeft);
                }
            }
            for (int j = n - 1; j >= 0; j--) {
                if (matrix[i][j] == '0') {
                    curRight = j;
                    right[j] = n;
                } else {
                    right[j] = Math.min(right[j], curRight);
                    res = Math.max(res, (right[j] - left[j]) * height[j]);
                }
            }
        }
        return res;
    }
}