leetcode难题之Maximal Rectangle

一，题目简述

leetcode第85题，Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

在一个只含有0和1的二维矩阵中，找出只含有1的最大矩形并返回其面积。

 

二，题目分析

在解决这一道题之前，让我们先看一下84题：Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram

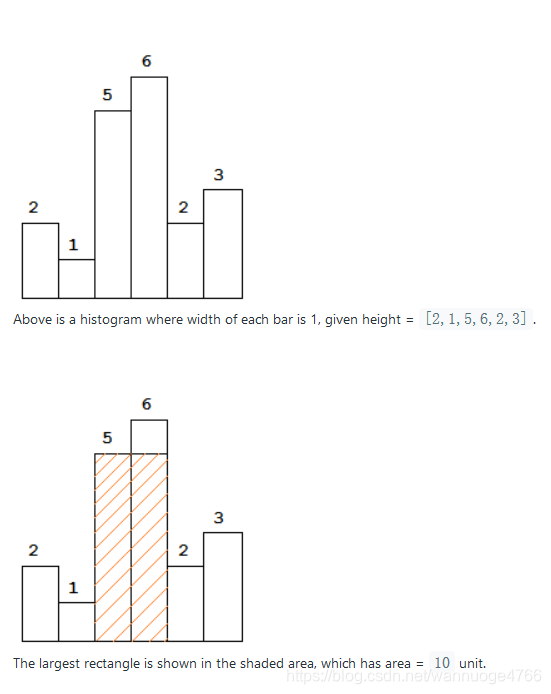
题目大意是找到条形图围住的最大面积，我们通过解决84题，然后找到84和85的联系，再通过84题的思路找到快速解决85题的方法。

在84题中，我们不难想到当我们从左到右遍历每一个条形图时，都计算下当前的最大面积；那我们可以观察到：如果条形图是递增，每下一个条形出现肯定会出现新的最大面积。这样的话我们可以利用递增栈辅助完成这道题，思路如下：

(1) 在height尾部添加一个高度为0的立柱，为了能计算所有条形图的情况，使递增栈倒空。

(2) 定义了一个递增栈stack，然后遍历时如果height[i] 小于stack.top()，出栈直到栈顶元素小于height[i]，并计算当前面积，再进栈。

(3) 由于比height[i]大的元素都出完了，height[i]又比栈顶元素大了，因此再次进栈。如此往复，直到遍历到最后那个高度为0的柱，触发最后的弹出以及最后一次面积的计算，此后stack为空。

(4) 返回面积最大值。

具体代码：

class Solution {
    public int largestRectangleArea(int[] heights) {
        if(heights == null || heights.length == 0)
            return 0;
        Stack<Integer> stack = new Stack<>();
        int res = 0;
        for(int i = 0; i <= heights.length;i++){
            int h = i == heights.length ? 0:heights[i];
            while(!stack.isEmpty() && h < heights[stack.peek()]){
                int height = heights[stack.pop()];
                int start = stack.isEmpty()?-1:stack.peek();
                int area = height * (i-start-1);
                res = Math.max(res,area);
            }
            stack.push(i);
        }
        return res;
    }
}

理解84题很重要，多画画图会加深理解，不过问题实质还是在借助一个递增栈计算可计算的最大面积，把时间效率提到最高

接下来讲为什么84题和85题会有联系

由题意可知，84题求条形图能围住的最大面积，85题是已知二元矩阵中1围住的最大面积。

我们可以想象一下如果84题的数据是动态的，即条形图的数据每天都有变化，而且变化是二元的即增加1或设置为0，然后我们要求过去几天条形图能围住的最大面积，就是85题的样子。

通过这个思路，我们可以想到，在m*n的矩阵中，相当于一个动态变化的m条形图要观察n天得到最大面积，84题算法时间复杂度乘以n即可。

三，题目解答

代码：

class Solution {
    public int maximalRectangle(char[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0) 
            return 0;
//初始化
        int[] height = new int[matrix[0].length];
        for(int i = 0; i < matrix[0].length; i ++){
            if(matrix[0][i] == '1') height[i] = 1;
        }
        
        int res = largestRectangleArea(height);

//重置整理height数组，并计算面积
        for(int i = 1; i < matrix.length; i ++){
            resetHeight(matrix, height, i);
            res = Math.max(res, largestRectangleArea(height));
         }
    
        return res;
    }
    
    private void resetHeight(char[][] matrix, int[] height, int idx){
        for(int i = 0; i < matrix[0].length; i++){
            if(matrix[idx][i] == '1') height[i] += 1;
            else height[i] = 0;
    }
}   
    
     public int largestRectangleArea(int[] heights) {
        if(heights == null || heights.length == 0)
            return 0;
        Stack<Integer> stack = new Stack<>();
        int res = 0;
        for(int i = 0; i <= heights.length;i++){
            int h = i == heights.length ? 0:heights[i];
            while(!stack.isEmpty() && h < heights[stack.peek()]){
                int height = heights[stack.pop()];
                int start = stack.isEmpty()?-1:stack.peek();
                int area = height * (i-start-1);
                res = Math.max(res,area);
            }
            stack.push(i);
        }
        return res;
    }
}

其中largeRectangleArea是84题原函数，resetHeight函数是通过新一行的数据调整height数组，主函数就根据我们上边的思路，先通过第一行初始化，然后剩下的行经过处理计算得到res的最大值。

四，题目回忆

计算条形图最大面积：递增栈

解决二元二维数组的一个思路->动态条形图->计算最大面积