从0实现树结构：存储与遍历

**

树及其深度/宽度优先遍历

1.树是递归定义的
2. 树的基本术语
• 结点的度：树中⼀个结点孩⼦的个数称为该结点的度。
• 树的度：树中结点最⼤的度数称为树的度。
• 树的⾼度（深度）：树中结点的最⼤层数称为树的⾼度（深度）。
• 路径：树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的，路径⻓度为序列中边的个数。
3.有序树和⽆序树
• 有序树：结点的⼦树按照从左往右的顺序排列，不能更改。
• ⽆序树：结点的⼦树之间没有顺序，随意更改。
4.有根树和⽆根树
• 有根树：树的根节点已知，是固定的。
• ⽆根树：树的根节点未知，谁都可以是根结点。

树的存储（孩子表示法）
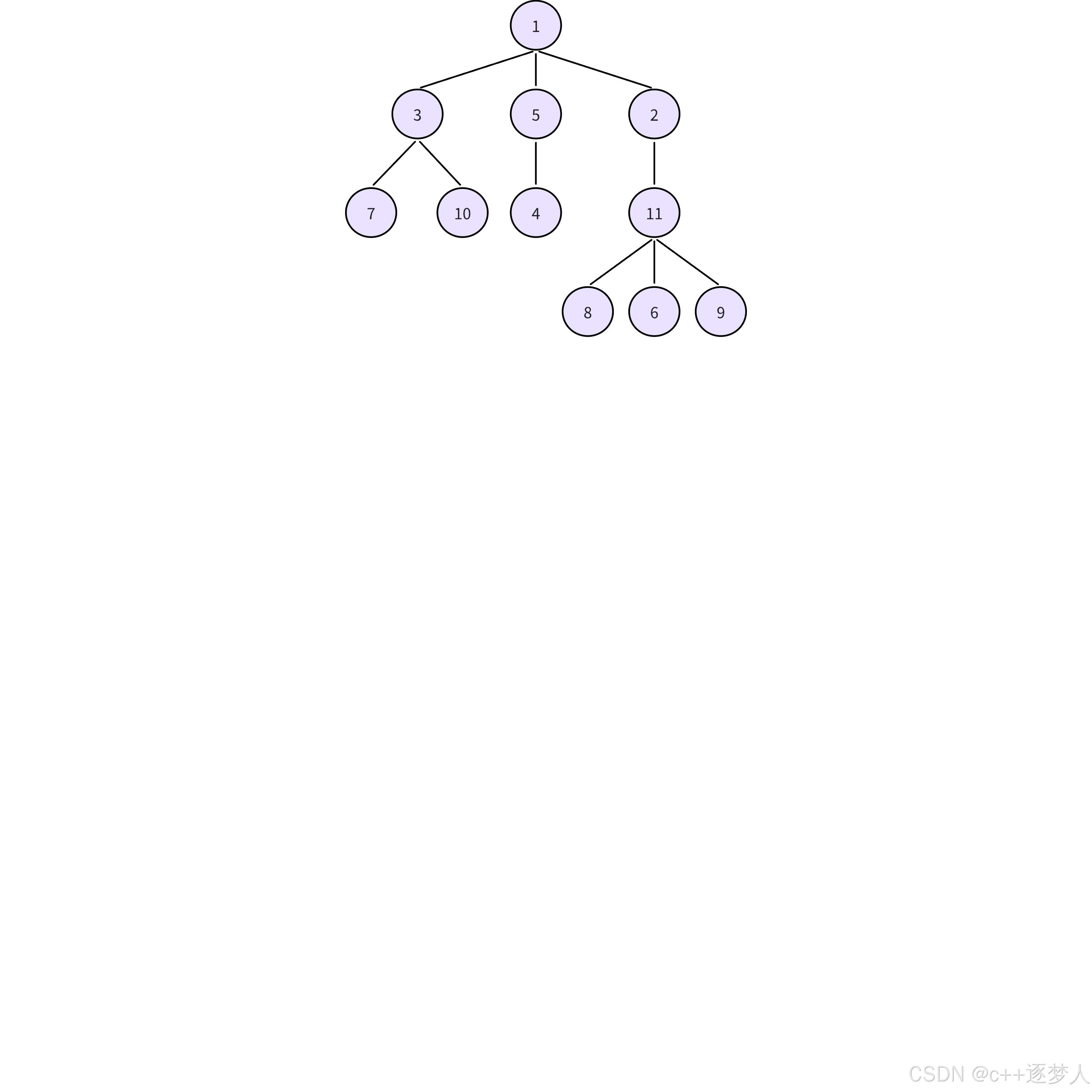
案例：
题⽬描述：
给定⼀棵树，该树⼀共有n个结点，编号分别是 1 ∼ n
输⼊描述：
第⼀⾏⼀个整数n ，表⽰n个结点。
接下来n-1⾏，每⾏两个整数u,v，表⽰u 和v之间有⼀条边。

2.1.⽤vector数组实现

#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5 + 10;
vector<int>p[N];
int main()
{
	int n;
	int a, b;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a >> b;
		p[a].push_back(b);
		p[b].push_back(a);

	}
	return 0;
}

2.2.链式前向星

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int h[N];//存储所有节点的哨兵位
int n[N], ne[N], id;
void add(int a, int b)
{
	id++;
	n[id] = b;
	ne[id] =h[a] ;
	h[a] = id;
}
int mian()
{
	int a, b, n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a >> b;
		add(a,b), add(b, a);
	}
	return 0;
}

3.1深度优先遍历-DFS
所谓深度优先，就是说每次都尝试向更深的节点⾛，也就是⼀条路⾛到⿊。
1.⽤vector数组实现

#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5 + 10;
vector<int>p[N];
bool st[N];
void dfs(int u)
{
	cout << u;
	st[u] = true;
	for (auto v: p[u])
	{
		if (!st[v])
		{
			dfs(v);
		}
	}
}

int main()
{
	int n;
	int a, b;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a >> b;
		p[a].push_back(b);
		p[b].push_back(a);
	}
	dfs(1);
	return 0;
}

2.链式前向星

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int h[N];//存储所有节点的哨兵位
int n[N], ne[N], id;
bool st[N];
void dfs(int u)
{
	cout << u;
	st[u] = true;
	for (int i = h[u]; i; i = ne[i])
	{
		int v = n[i];
		if (!st[v])
		{
			dfs(v);
		}
	}
}


void add(int a, int b)
{
	id++;
	n[id] = b;
	ne[id] =h[a] ;
	h[a] = id;
}
int main()
{
	int a, b, n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a >> b;
		add(a,b), add(b, a);
	}
	dfs(1);
	return 0;
}

3.2宽度优先遍历-BFS
所谓宽度优先。就是每次都尝试访问同⼀层的节点。如果同⼀层都访问完
了，再访问下⼀层。
1.⽤vector数组实现

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
vector<int>p[N];
bool st[N];
void bfs()
{
	queue<int>q;
	q.push(1);
	st[1] = true;
	while (q.size())
	{
		auto u = q.front(); q.pop();
		cout << u;
		for (auto v: p[u])
		{
			if (!st[v])
				{
					q.push(v);
					st[v] = true;
				}
		}
	}
	
}
int main()
{
	int n;
	int a, b;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a >> b;
		p[a].push_back(b);
		p[b].push_back(a);
	}
	bfs();
	return 0;
}

2. 链式向前星

#include<iostream>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
int h[N];//存储所有节点的哨兵位
int n[N], ne[N], id;
bool st[N];
void bfs()
{
	queue<int>q;
	q.push(1);
	st[1] = true;
	while (q.size())
	{
		auto u = q.front(); q.pop();
		cout << u;
		for (int i = h[u]; i; i = ne[i])
		{
			int v = n[i];
			if (!st[v])
			{
				q.push(v);
				st[v] = true;
			}
		}
	}
}
void add(int a, int b)
{
	id++;
	n[id] = b;
	ne[id] =h[a] ;
	h[a] = id;
}
int main()
{
	int a, b, n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a >> b;
		add(a,b), add(b, a);
	}
	bfs();
	return 0;
}. 

下一篇二叉树