三角学
- 用弧度度量的角与三角函数的基本知识
- 实轴上的三角函数(不只是介于0∘0^\circ0∘和90∘90^\circ90∘)的角
- 三角函数的图像
- 三角恒等式
基本知识
旋转一周为2π2\pi2π,因为半径为1个单位的圆的周长为2π2\pi2π个单位。事实上,这个圆的一个扇形的弧长就是这个扇形的圆心角的弧度
几个重要的角
| 角度制 | 弧度制 |
|---|---|
| 90∘90^\circ90∘ | π2\frac{\pi}{2}2π |
| 180∘180^\circ180∘ | π\piπ |
| 270∘270^\circ270∘ | 3π2\frac{3\pi}{2}23π |
角度制和弧度制转换的公式
用弧度度量的角=π180×用度计量的角
用弧度度量的角=\frac{\pi}{180}\times用度计量的角
用弧度度量的角=180π×用度计量的角
由三角形定义三角函数
假设有一个直角三角形,除直角外的一角被记为θ\thetaθ
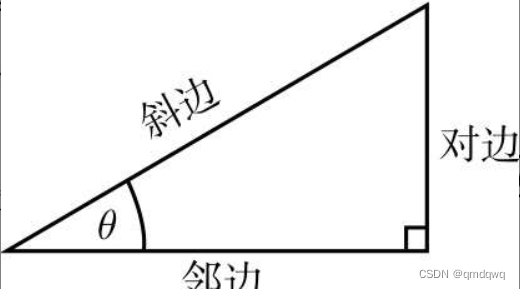
那么基本公式为
sin(θ)=对边斜边
\sin(\theta)=\frac{对边}{斜边}
sin(θ)=斜边对边
cos(θ)=邻边斜边 \cos(\theta)=\frac{邻边}{斜边} cos(θ)=斜边邻边
tan(θ)=对边邻边 \tan(\theta)=\frac{对边}{邻边} tan(θ)=邻边对边
对边就是对着角θ\thetaθ的边,邻边则是挨着角θ\thetaθ的边,斜边是最长的那条边,并始终对着直角
他们的倒数函数分别为
余割
csc(x)=1sin(x)
\csc(x)=\frac{1}{\sin(x)}
csc(x)=sin(x)1
正割
sec(x)=1cos(x)
\sec(x)=\frac{1}{\cos(x)}
sec(x)=cos(x)1
余切
cot(x)=1tan(x)
\cot(x)=\frac{1}{\tan(x)}
cot(x)=tan(x)1
以下角的三角函数值需要牢记

那么我们该如何求任意角的正弦或者余弦呢,下面这张图给了很好的回答
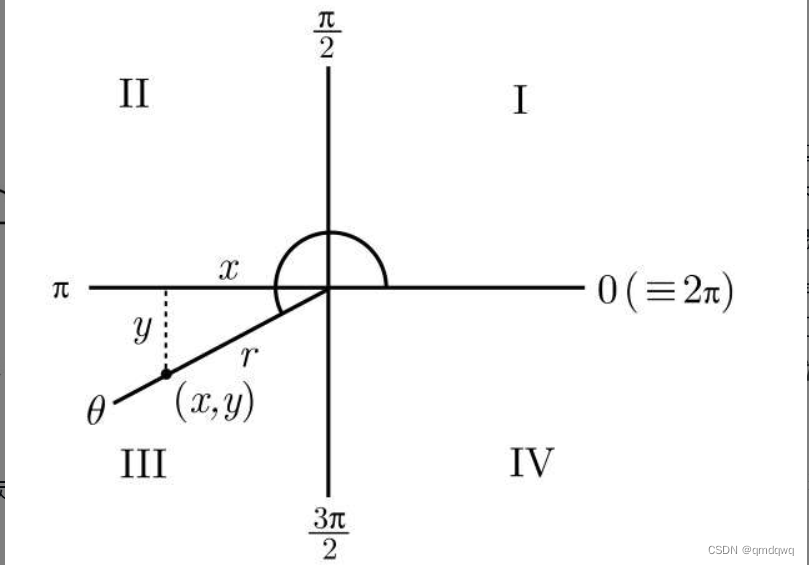
根据这张图,我们就可以定义如下三个三角函数
sin(θ)=yr
\sin(\theta)=\frac{y}{r}
sin(θ)=ry
cos(θ)=xr \cos(\theta)=\frac{x}{r} cos(θ)=rx
tan(θ)=yx \tan(\theta)=\frac{y}{x} tan(θ)=xy
如果我们选取了另外一个点,上述比值不会受到任何影响,为方便起见,甚至经常假设r=1,这样得到的点(x,y)会落在单位圆上。,因此上述公式可以化简为
sin(θ)=y
\sin(\theta)=y
sin(θ)=y
cos(θ)=x \cos(\theta)=x cos(θ)=x
tan(θ)=yx \tan(\theta)=\frac{y}{x} tan(θ)=xy
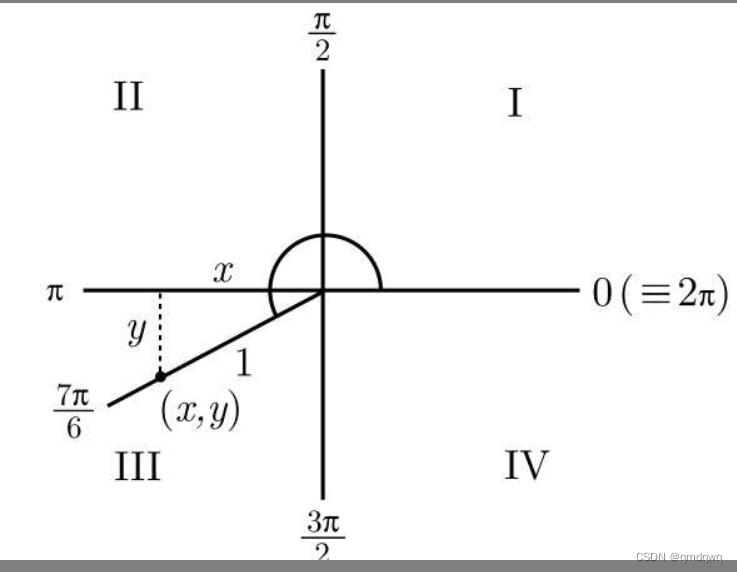
假设我们要求sin(7π6)\sin(\frac{7\pi}{6})sin(67π)
-
首先,画一个如下图所示的直角坐标系
-
选取该射线上的一点,该点到原点的距离r=1
-
然后我们从该点至x轴做了一条垂线
*
-
我们目前已知r=1,只需再知道y等于多少,即可知道该角的正弦
-
这里我们就需要用到7π6\frac{7\pi}{6}67π的参考角,一般来说θ\thetaθ的参考角是在表示角θ\thetaθ的射线和x轴之间的最小角,它必定介于0到π2\frac{\pi}{2}2π
-
这里7π6\frac{7\pi}{6}67π的参考角为7π6−π=π6\frac{7\pi}{6}-\pi=\frac{\pi}{6}67π−π=6π
-
根据上文我们总结的公式可得y=sin(π6)=12y=\sin(\frac{\pi}{6})=\frac{1}{2}y=sin(6π)=21,但请注意,y是有正负的,所以,因为7π6\frac{7\pi}{6}67π在第三象限,所以y应该为−12-\frac{1}{2}−21
-
所以sin(7π6)=−12\sin(\frac{7\pi}{6})=-\frac{1}{2}sin(67π)=−21
ASTC方法
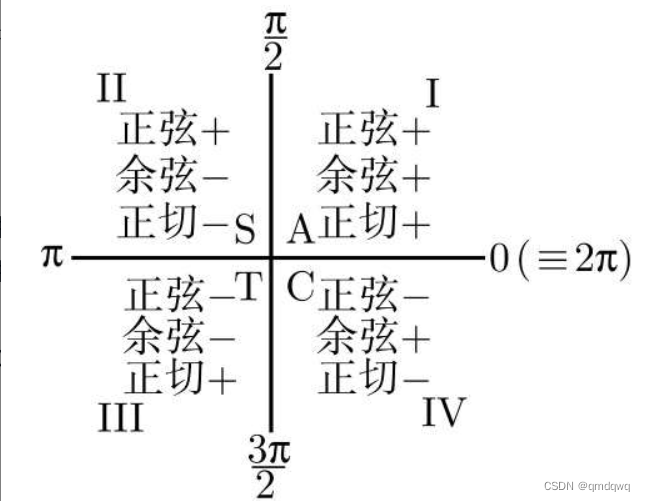
所谓ASTC分别对应着角在第一象限到第四象限中正弦、余弦、正切的正负情况。该方法以每个象限中为正值的首字母命名
A: all
S: sin
t: tan
c: cos
也就是说,在第一象限中,三个函数全为正值;第二象限中,只有正弦为正值;第三象限中,只有正切为正值;第四象限中,只有余弦为正值
但该方法对角0,π2\frac{\pi}{2}2π,π\piπ,3π2\frac{3\pi}{2}23π无效,因为它们都位于左标轴上
使用该方法的步骤简单总结如下(这里我们不讨论在坐标轴上的情况)
- 画出象限图,确定角的位置在第几象限
- 找出该角的参考角
- 根据常用角的三角函数求出参考角的三角函数值
- 使用ASTC来确定正负
[0,2π][0,2\pi][0,2π]以外的三角函数
如何取大于2π2\pi2π或小于0的角的三角函数呢?
仔细想象我们旋转360度,是不是面向的方向不变呢?在三角函数中,加上或减去2π2\pi2π的倍数,最终的三角函数值也是不变的,因此我们可以加上或减去2π2\pi2π的倍数,直到得到的角落在[0,2π][0,2\pi][0,2π],就可以求了
假设有一个角为n,所有跟它等价的角我们可以写为π/2+2πn{\pi/2+2\pi n}π/2+2πn,,其中n可以取所有整数
另外,逆时针旋转−nπ-n\pi−nπ实际上就是顺时针旋转nπn\pinπ
三角函数的图像
记住正弦、余弦和正切函数的图像非常有用,这些函数都是周期的,这意味着,它们会从左到右反复地重复自己
下面是正弦函数在[0,2π][0,2\pi][0,2π]的图像
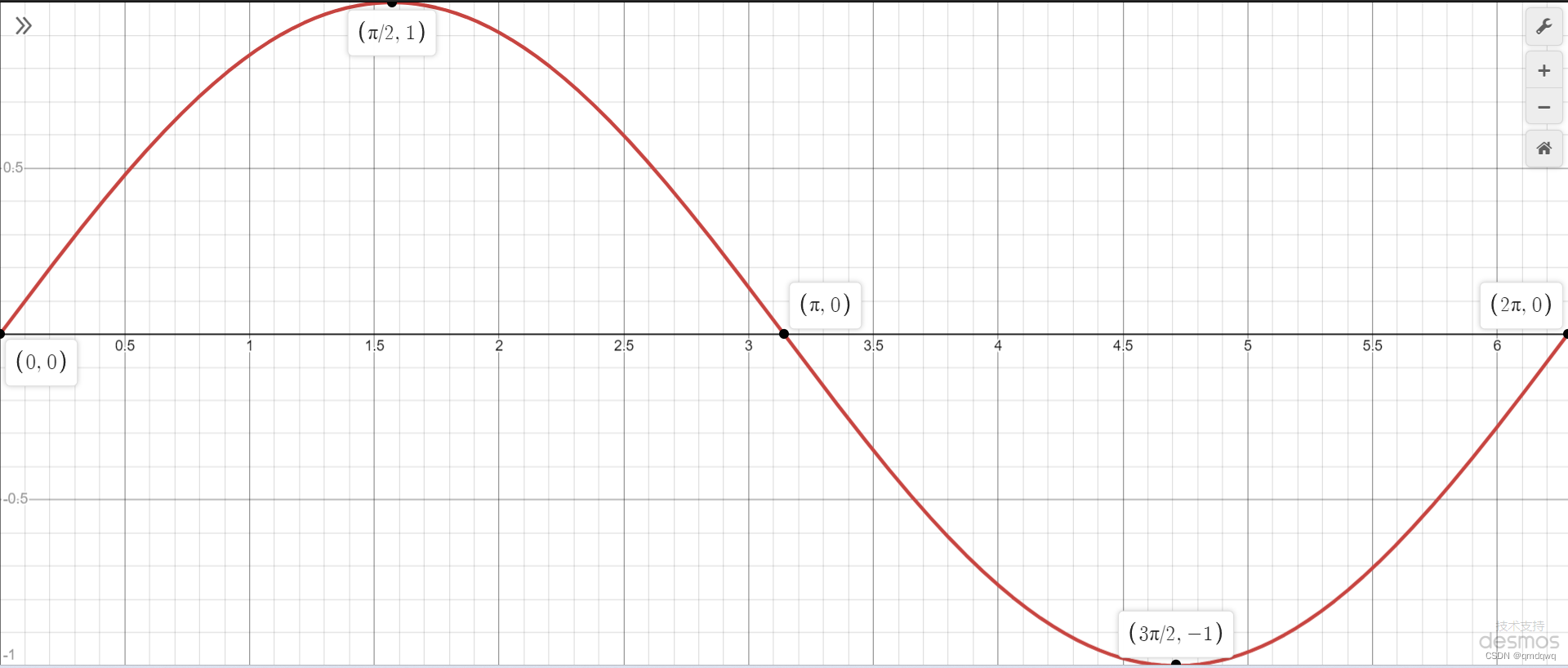
由于sin(x)\sin(x)sin(x)以2π2\pi2π为单位重复,我们说sin(x)是x的周期函数,其周期为2π2\pi2π,可以利用这一点来看看在[0,2π][0,2\pi][0,2π]外的图像,由于这里会无限重复,所以我们只看在[−3π,3π][-3\pi,3\pi][−3π,3π]的图像
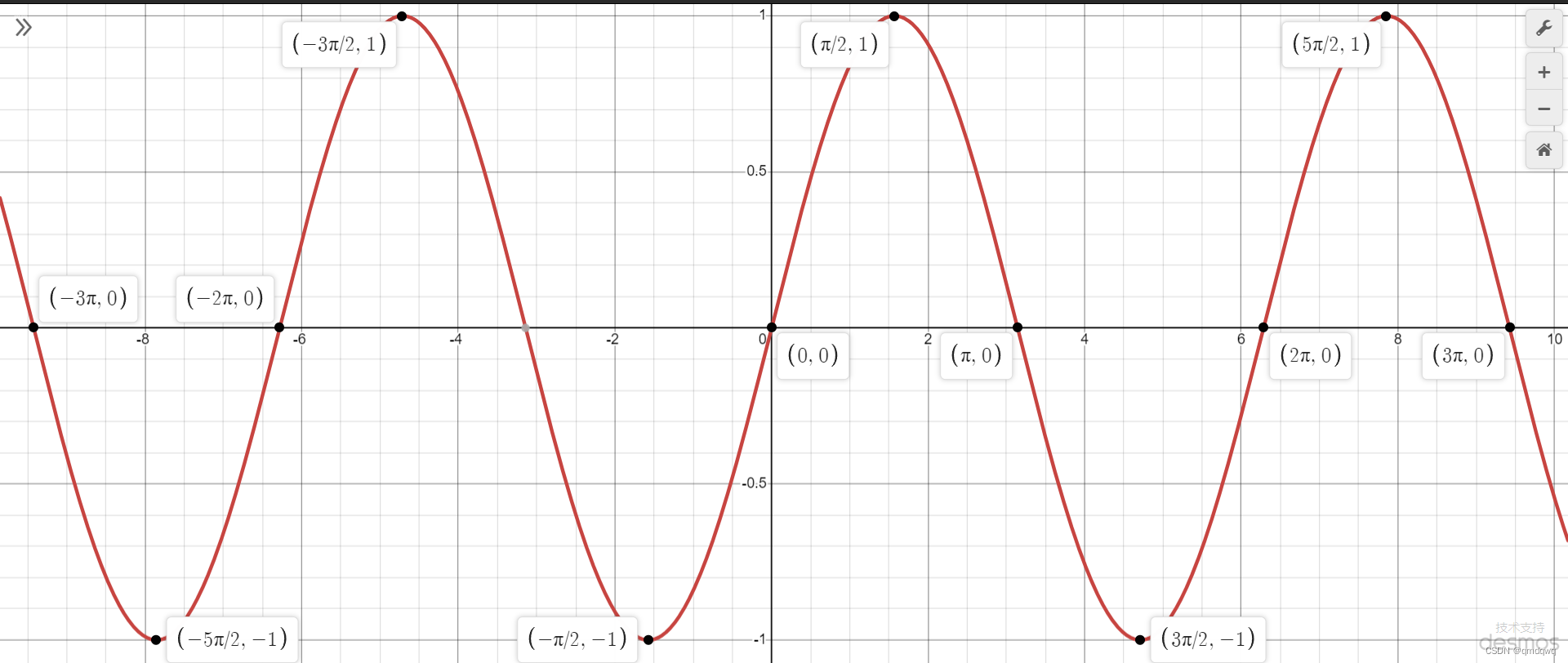
该图像关于原点有180∘180^\circ180∘点对称,即该函数是一个奇函数
下面是余弦函数在[0,2π][0,2\pi][0,2π]的图像
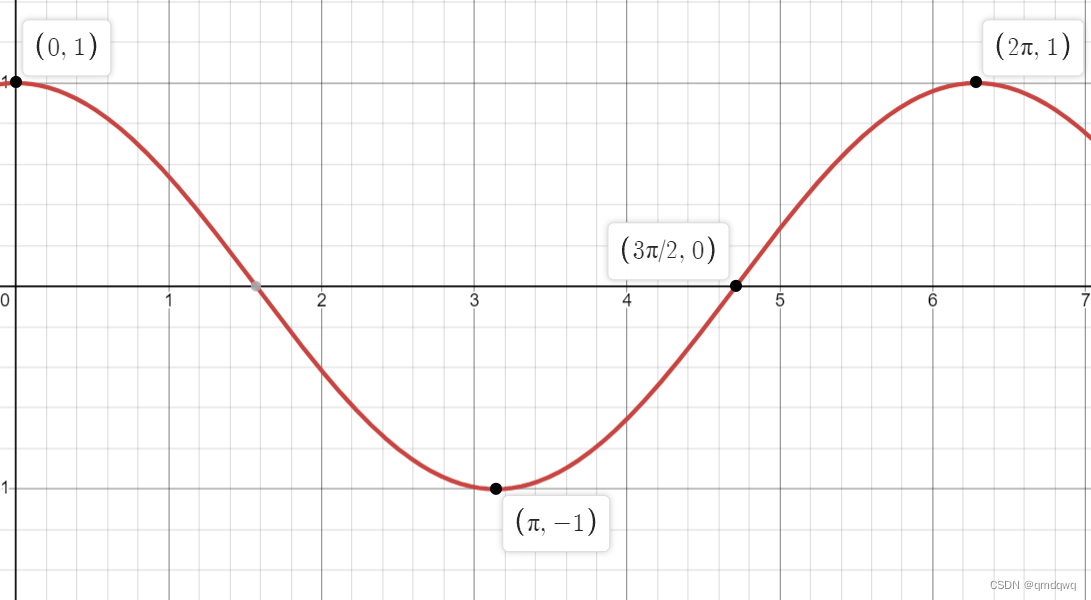
利用cos(x)\cos(x)cos(x)的周期为2π2\pi2π这一事实,画出该函数在[−3π,3π][-3\pi,3\pi][−3π,3π]的图像
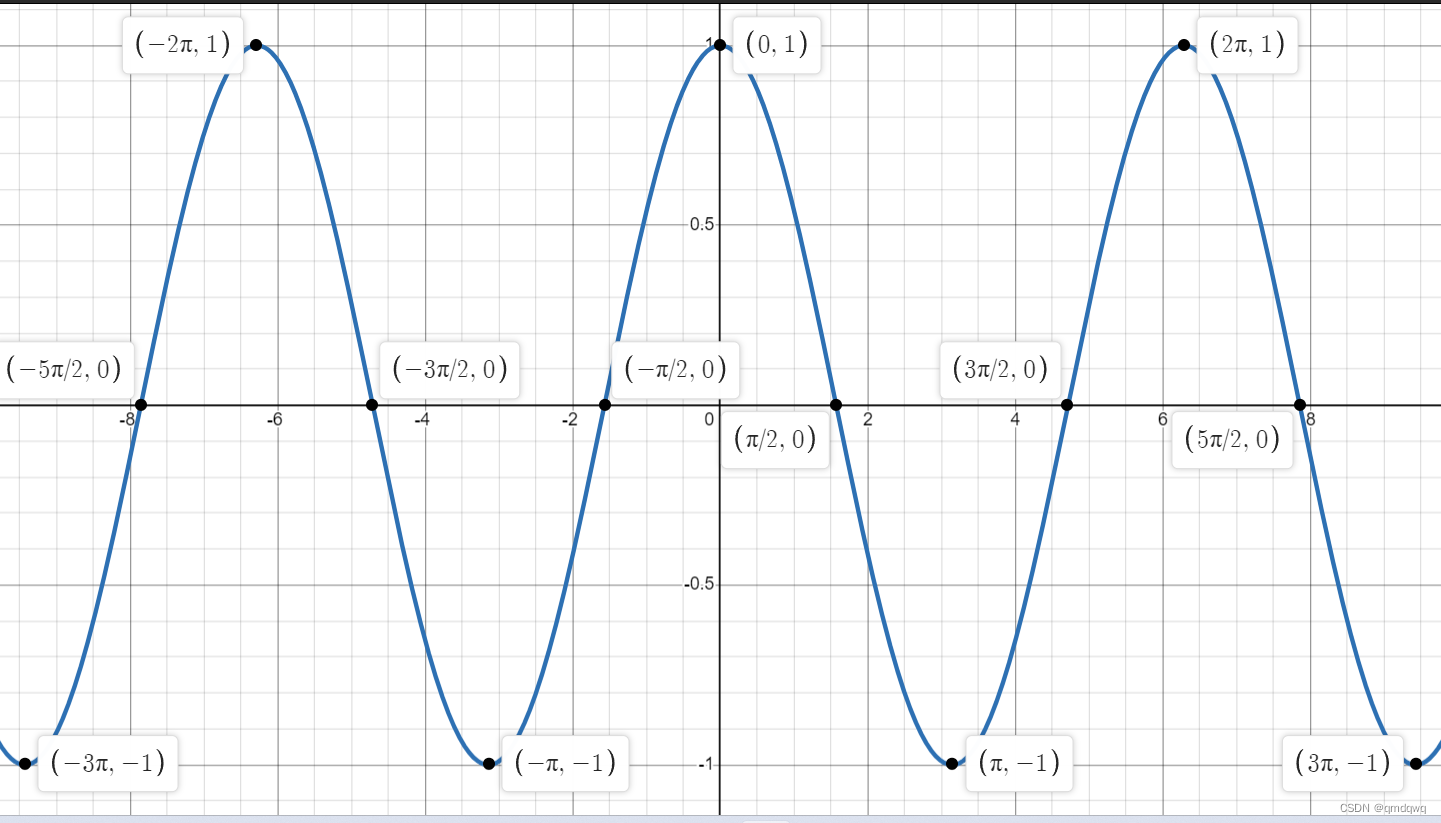
可以看出该图像关于y轴有镜面对称性,因此,我们可知cos(x)\cos(x)cos(x)是偶函数
与正弦函数和余弦函数不同的是,正切函数的周期是π\piπ且其有垂直渐近线,下面是正切函数的图像
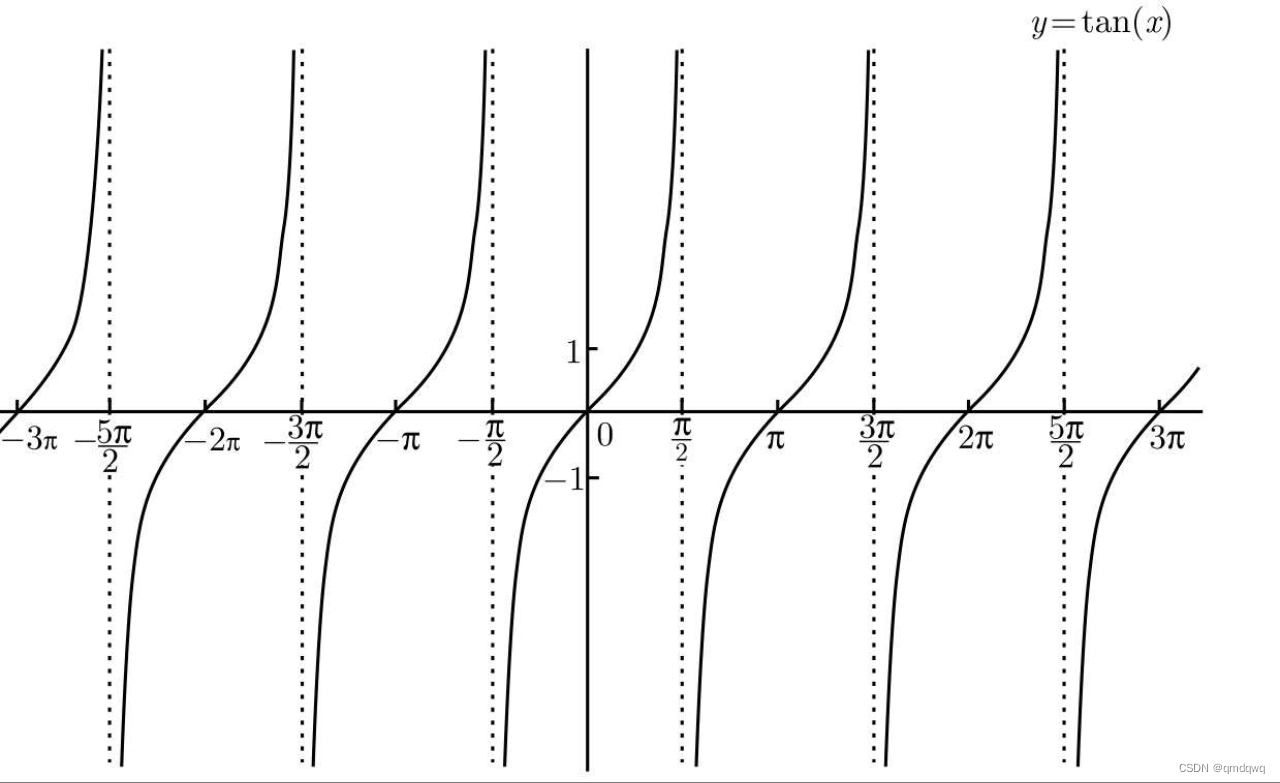
下面分别是正割、余割、余切的函数图像
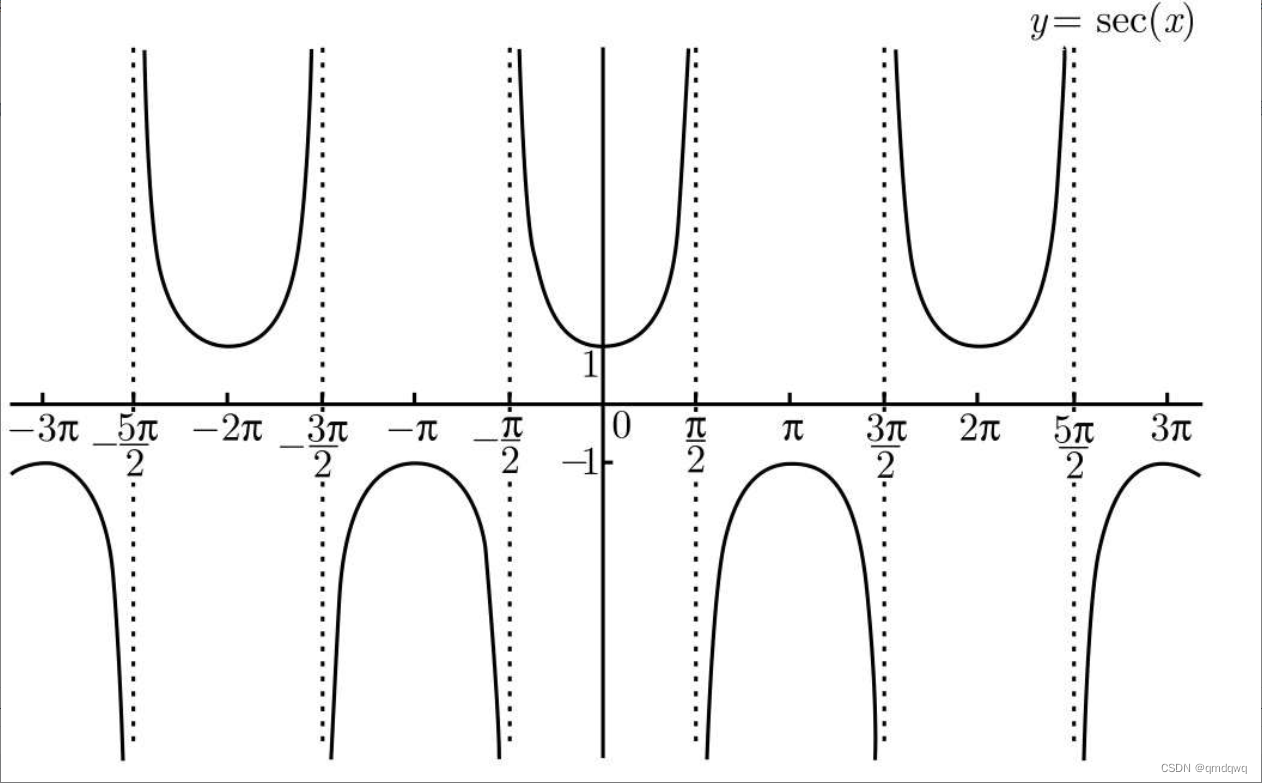
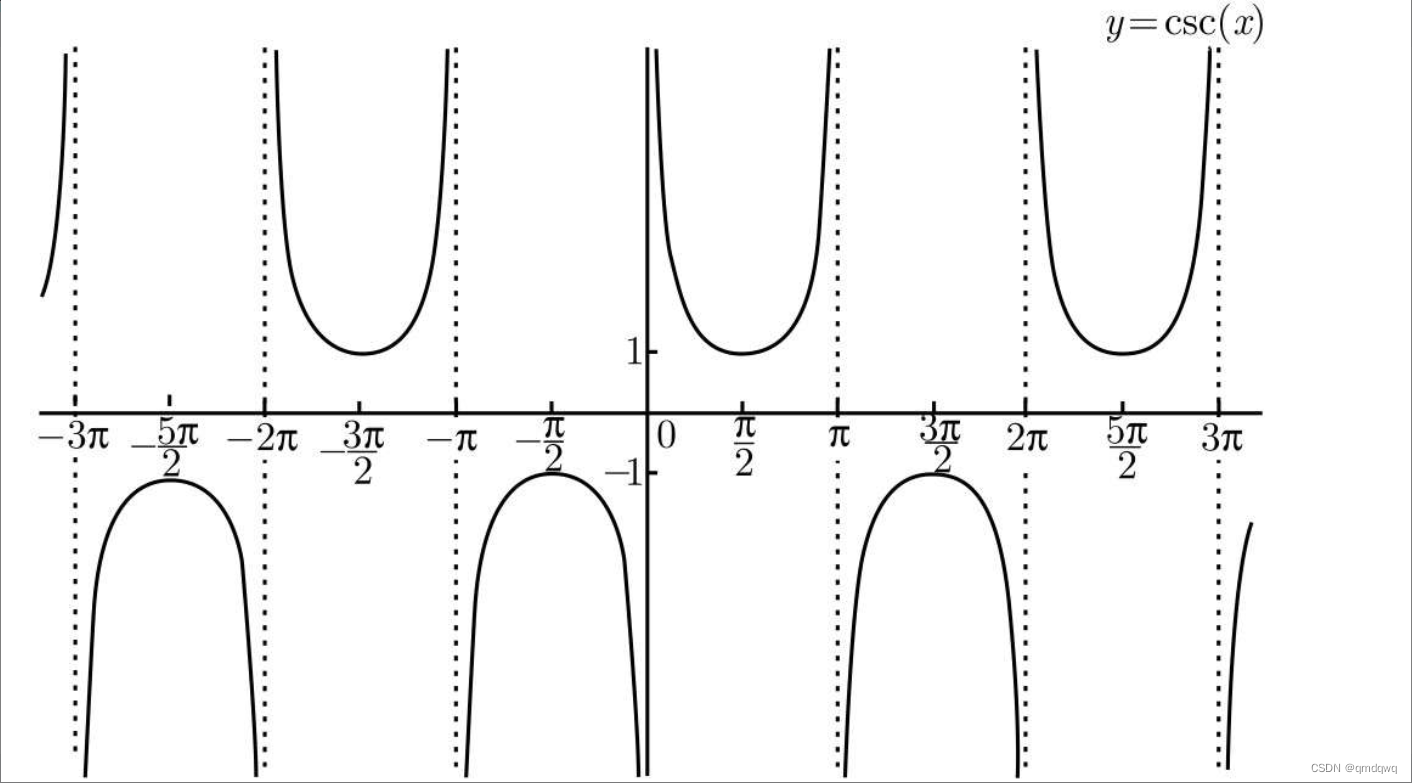
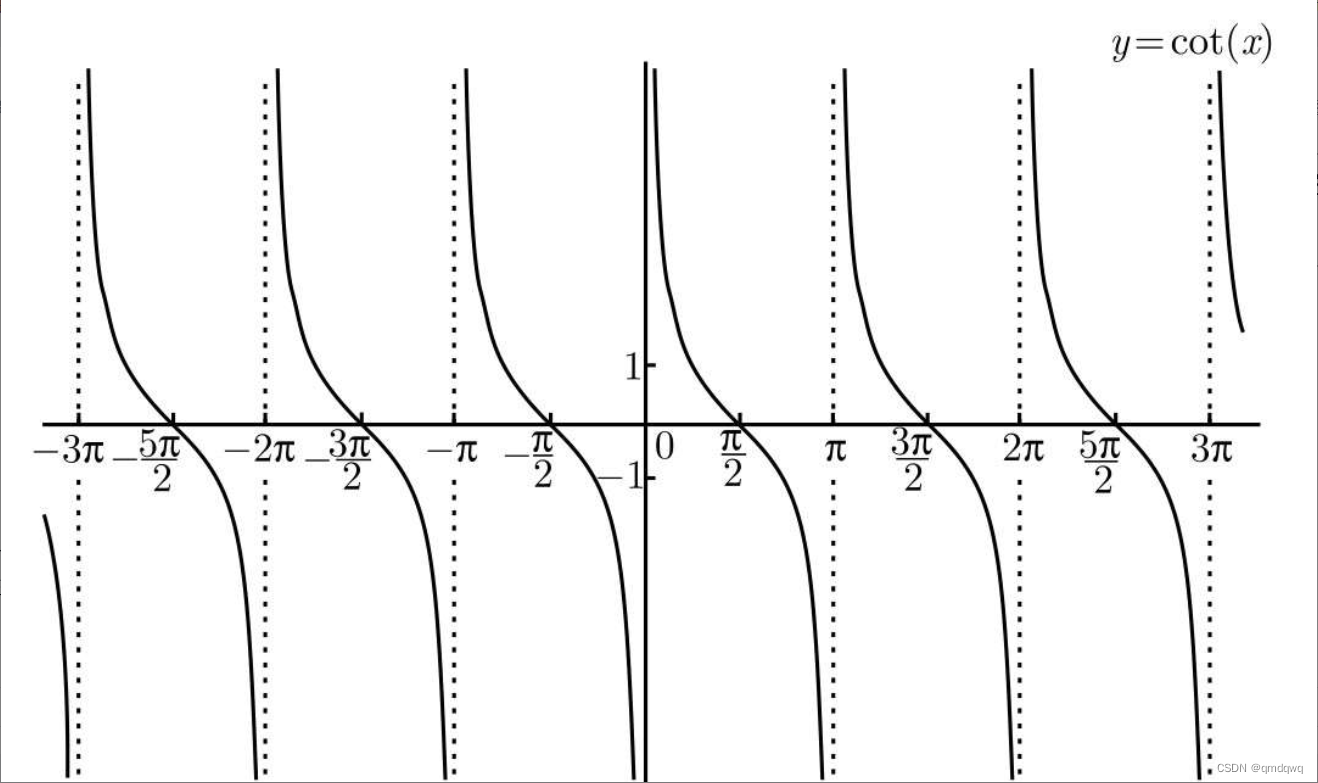
总结
sin(x)\sin(x)sin(x)、tan(x)\tan(x)tan(x)、cot(x)\cot(x)cot(x)、csc(x)\csc(x)csc(x)都是奇函数。cos(x)cos(x)cos(x)、sec(x)\sec(x)sec(x)都是偶函数
三角恒等式
正切和余切可以用正弦和余弦表示
正切
tan(x)=sin(x)cos(x)
\tan(x)=\frac{\sin(x)}{\cos(x)}
tan(x)=cos(x)sin(x)
余切
cot(x)=cos(x)sin(x)
\cot(x)=\frac{\cos(x)}{\sin(x)}
cot(x)=sin(x)cos(x)
毕达哥拉斯定理
cos2(x)+sin2(x)=1
\cos^2(x)+\sin^2(x)=1
cos2(x)+sin2(x)=1
将这个等式两边同时除以cos2(x)\cos^2(x)cos2(x),将得到如下等式
1+tan2(x)=sec2(x)
1+\tan^2(x)=sec^2(x)
1+tan2(x)=sec2(x)
如果将毕达哥拉斯定义等式两边同时处于sin2(x)sin^2(x)sin2(x),将得到以下等式
cot2(x)+1=csc2(x)
\cot^2(x)+1=\csc^2(x)
cot2(x)+1=csc2(x)
其他关系
一些函数的名字以音节co开头,这表示互余,有如下一般关系
三角函数(x)=co三角函数(π2−x)
三角函数(x)=co三角函数(\frac{\pi}{2}-x)
三角函数(x)=co三角函数(2π−x)
特别地,有如下几条公式
sin(x)=cos(π2−x)
sin(x)=cos(\frac{\pi}{2}-x)
sin(x)=cos(2π−x)
tan(x)=cot(π2−x) \tan(x)=\cot(\frac{\pi}{2}-x) tan(x)=cot(2π−x)
sec(x)=csc(π2−x) \sec(x)=\csc(\frac{\pi}{2}-x) sec(x)=csc(2π−x)
下面这组恒等式也很重要
sin(A−B)=sin(A)cos(B)−cos(A)sin(B)
\sin(A-B)=\sin(A)\cos(B)-\cos(A)\sin(B)
sin(A−B)=sin(A)cos(B)−cos(A)sin(B)
cos(A+B)=cos(A)cos(B)−sin(A)sin(B) \cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B) cos(A+B)=cos(A)cos(B)−sin(A)sin(B)
sin(A+B)=sin(A)cos(B)+cos(A)sin(B) \sin(A+B)=\sin(A)\cos(B)+\cos(A)\sin(B) sin(A+B)=sin(A)cos(B)+cos(A)sin(B)
cos(A−B)=cos(A)cos(B)+sin(A)sin(B) \cos(A-B)=\cos(A)\cos(B)+\sin(A)\sin(B) cos(A−B)=cos(A)cos(B)+sin(A)sin(B)
上面这组恒等式中,我们令A=B=x,再利用毕达哥拉斯定理,就会得到倍角公式
sin(2x)=2sin(x)cos(x)
\sin(2x)=2\sin(x)\cos(x)
sin(2x)=2sin(x)cos(x)
cos(2x)=2cos2(x)−1=1−2sin2(x) \cos(2x)=2\cos^2(x)-1=1-2\sin^2(x) cos(2x)=2cos2(x)−1=1−2sin2(x)





















 7164
7164

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








