数据结构--线段树

1 线段树定义

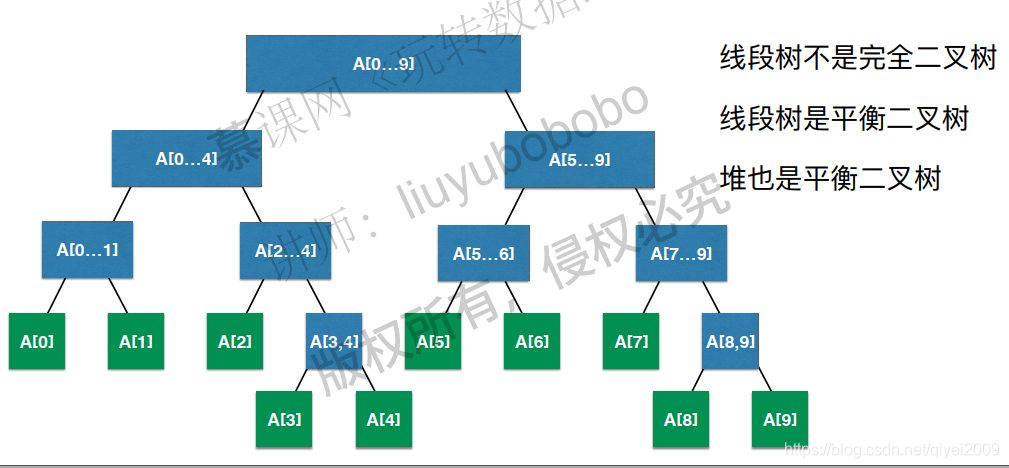
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。 [1]
对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

2 线段树实现

1 创建线段树
创建一颗线段树来讲，还是使用递归的方式
线段树使用两个数组
data[]表示真实的元素
tree[]表示创建好后的线段树，并且每个tree[i]对应的值与业务相关

    /**
     * 融合操作定义
     * 对于不同的业务场景，融合操作定义不一样，例如求和，求最大值，最小值
     * @param <E>
     */
    public interface Merger<E>{
        /**
         * 两个元素的融合操作
         * @param a
         * @param b
         * @return
         */
        E merge(E a,E b);
    }

    /**
     * 线段树元素存储区
     */
    private E[] data;
    /**
     * 线段树
     */
    private E[] tree;
    /**
     * 融合器
     */
    private Merger<E> merger;

    public SegmentTree(E[] array,Merger<E> merger) {
        this.data = (E[]) new Object[array.length];
        System.arraycopy(array,0,data,0,array.length);
        tree = (E[]) new Object[4 * array.length];

        this.merger = merger;
        buildSegmentTree(0,0,data.length - 1);
    }

    /**
     * 在index处创建[l...r]的线段树
     * @param treeIndex
     * @param l 左边界
     * @param r 右边界
     */
    private void buildSegmentTree(int treeIndex, int l, int r) {

        //数据边界检查
        if (treeIndex < 0 || treeIndex >= tree.length){
            return;
        }

        if (l < 0 || l >= data.length){
            return;
        }

        if (r < 0 || r >= data.length){
            return;
        }

        //无法再分割了，已经到了最小区间
        if (l == r){
            tree[treeIndex] = data[l];
            return;
        }

        int leftChildIndex = indexLeftChild(treeIndex);
        int rightChildIndex = indexRightChild(treeIndex);
        int mid = l + ( r - l ) / 2;
        //创建左子树和右子树的线段树
        buildSegmentTree(leftChildIndex,l,mid);
        buildSegmentTree(rightChildIndex,mid + 1,r);
        //根节点是两个子节点的融合值
        tree[treeIndex] = merger.merge(tree[leftChildIndex],tree[rightChildIndex]);
}
	….
    /**
     * 返回二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
     * @param index
     * @return
     */
    private int indexLeftChild(int index){
        return 2 * index + 1;
    }

    /**
     * 返回二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
     * @param index
     * @return
     */
    private int indexRightChild(int index){
        return 2 * index + 2;
    }

2 线段树的查询
线段树最主要的操作就是查询某个区间的值。因此定义如下接口

/**
 * 查询线段树[l..r]的结果
 * @param l
 * @param r
 * @return
 */
public E query(int l,int r){
    if (l < 0 || l >= data.length || r < 0 || r >= data.length){
        throw new IllegalArgumentException("illegalArgument for l r");
    }
    return query(0,0,data.length - 1,l,r);
}

/**
 * 在treeIndex的线段树中查询[l..r]区间结果
 * @param treeIndex
 * @param l
 * @param r
 * @param queryL
 * @param queryR
 * @return
 */
private E query(int treeIndex,int l,int r,int queryL,int queryR){

    //查询到结果了
    if (l == queryL && r == queryR){
        return tree[treeIndex];
    }

    int leftChildIndex = indexLeftChild(treeIndex);
    int rightChildIndex = indexRightChild(treeIndex);
    int mid = l + ( r - l ) / 2;
    //全部在左子树
    if (queryR <= mid){
        return query(leftChildIndex,l,mid,queryL,queryR);
    } else if (queryL > mid + 1){
        //全在右子树
        return query(rightChildIndex,mid + 1,r,queryL,queryR);
    }

    //左右子树都有
    E leftResult = query(leftChildIndex,l,mid,queryL,mid);
    E rightResult = query(rightChildIndex,mid + 1,r,mid + 1,queryR);
    return merger.merge(leftResult,rightResult);
}

3 更新线段树

有时需要对线段树中的某个值进行更新

/**
 * 修改线段树索引为index处的值
 * @param index
 * @param e
 */
public void set(int index,E e){
    set(0,0,size() - 1,index,e);
}

/**
 * 修改treeIndex为根节点的线段树的值
 * @param treeIndex
 * @param l
 * @param r
 * @param index
 * @param e
 */
private void set(int treeIndex,int l,int r,int index,E e){

    if (l == r){
        tree[treeIndex] = e;
        return;
    }

    int leftChildIndex = indexLeftChild(treeIndex);
    int rightChildIndex = indexRightChild(treeIndex);

    int mid = l + ( r - l ) / 2;
    if (index <= mid){
        set(leftChildIndex,l,mid,index,e);
    } else {
        set(rightChildIndex,mid + 1,r,index,e);
    }

    tree[treeIndex] = merger.merge(tree[leftChildIndex],tree[rightChildIndex]);
}

4 线段树时间复杂度分析
线段树是一颗平衡二叉树，因此各种操作的时间复杂度是O(logn)

3 线段树应用

1 区间染色及查询问题

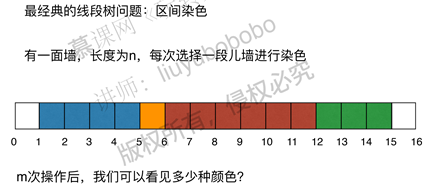
2 基于区间的统计查询