SVM核函数大揭秘：一文读懂线性核、多项式核、RBF核和Sigmoid核（附Python代码）

最新推荐文章于 2025-07-22 14:04:39 发布

原创最新推荐文章于 2025-07-22 14:04:39 发布 · 2.3k 阅读

31 ·

CC 4.0 BY-SA版权

文章标签：

#支持向量机 #python #机器学习 #SVN #svm

前言：为什么核函数是SVM的"魔法棒"？🧙‍♂️

在支持向量机(SVM)的世界里，核函数就像哈利波特的魔法棒——轻轻一挥，就能让线性不可分的数据变得服服帖帖！今天我们就来深度解析SVM最常用的四大核函数，用最通俗的语言+最直观的代码，带你玩转核技巧。

一、核函数是什么？🤔

简单来说，核函数就是SVM的"翻译官"：

🌍 把原始数据从低维空间"翻译"到高维空间
🎯 让原本线性不可分的数据在高维空间中变得可分
🚀 无需显式计算高维坐标，直接计算相似度

二、四大核函数深度对比🆚

1. 线性核 (Linear Kernel)📏

公式：

核心原理：

直接计算原始特征空间的内积，不进行非线性变换

优点：

计算效率高：复杂度低，适合大规模数据集
可解释性强：支持向量对应关键样本，决策边界清晰

缺点：

无法处理非线性问题：环形或月牙形数据分类效果差

适用场景：

数据线性可分（如文本分类、高维稀疏数据）
特征维度远高于样本量（如TF-IDF文本特征）

实战表现：

在鸢尾花数据集分类中准确率约88.3%，低于非线性核函数

代码示例：

from sklearn.svm import SVC
model = SVC(kernel='linear')  # 默认C=1.0
model.fit(X_train, y_train)

2. 多项式核 (Polynomial Kernel)🎢

公式：

其中 γ 为缩放系数，r 为常数项，d 为多项式阶数

核心原理：

通过升维将数据映射到高维空间实现线性可分

优点：

灵活性：通过调整 d 控制模型复杂度

缺点：

参数敏感：高阶 d 易导致过拟合和计算爆炸（复杂度 O(d!)）
调参复杂：需优化 γ,r,d 三个参数

适用场景：

中等规模数据集（如带明显多项式关系的数据分布）
数据存在多项式关系时
需要非线性边界但不太复杂的情况

实战表现：

在鸢尾花分类中准确率约95%，但决策边界易波动

代码示例：

model = SVC(kernel='poly', degree=3, gamma='scale', coef0=1)

3. 高斯核/RBF核 (Gaussian/RBF Kernel)🌌

公式：

其中 γ 控制高斯函数宽度

核心原理：

将数据映射到无限维空间，通过局部相似性划分边界

优点：

强大拟合能力：在多数数据集上表现最优（如鸢尾花分类准确率98.3%）
参数较少：仅需调整 γ 和惩罚参数 C

缺点：

过拟合风险：γ 过大时决策边界过于复杂
计算开销大：样本量大时训练慢（复杂度）

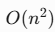适用场景：

非线性问题（如环形数据）
图像分类（如MNIST）
生物信息学数据

调参要点：

γ 增大→模型更敏感→易过拟合；γ 减小→决策边界平滑→易欠拟合

代码示例：

model = SVC(kernel='rbf', gamma=0.1, C=1.0)

4. Sigmoid核 (Sigmoid Kernel)🧠

公式：

其中 γ 为缩放系数，r 为截距

核心原理：

模拟神经网络激活函数，输出双曲正切值

优点：

与神经网络兼容：可用于迁移学习场景

缺点：

表现不稳定：参数选择不当易导致低准确率（如月牙形数据分类准确率仅66.7%）
非正定风险：核矩阵可能不满足Mercer条件，影响收敛性

适用场景：

特定二分类问题（如模拟神经网络结构）
需要概率输出的特殊情况

实战建议：

需严格调参，否则效果可能不如随机猜测

代码示例：

model = SVC(kernel='sigmoid', gamma='scale', coef0=0)

三、核函数对比总表📊

核函数	适用数据	参数复杂度	计算效率	典型准确率	推荐场景
线性核	线性可分、高维稀疏	低（仅 C）	⭐⭐⭐⭐⭐	中（~88%）	文本分类、大规模数据
多项式核	中度非线性	高（γ,r,d）	⭐⭐	中高（~95%）	已知数据多项式关系
高斯核	强非线性	中（γ,C）	⭐⭐	高（~98%）	默认首选，复杂模式
Sigmoid核	特定二分类	中（γ,r）	⭐⭐⭐	低（~66%）	神经网络迁移场景

选型优先级建议：
1. 优先尝试RBF核（通用性强） → 2. 线性数据用线性核（高效可解释） → 3. 特定需求选多项式/Sigmoid核（需严格验证）

四、实战演示：不同核函数的效果对比🎯

1. 生成测试数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons, make_circles
from sklearn.svm import SVC

X, y = make_circles(n_samples=200, noise=0.1, factor=0.4, random_state=42)

2. 可视化函数

def plot_decision_boundary(model, X, y):
    # 创建网格点
    xx, yy = np.meshgrid(np.linspace(-1.5, 1.5, 200), np.linspace(-1.5, 1.5, 200))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # 绘制决策边界
    plt.contourf(xx, yy, Z, alpha=0.4)
    plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor='k')
    plt.title(f"Kernel: {model.kernel}")

3. 测试不同核函数

kernels = ['linear', 'poly', 'rbf', 'sigmoid']
plt.figure(figsize=(12, 10))

for i, kernel in enumerate(kernels):
    plt.subplot(2, 2, i+1)
    model = SVC(kernel=kernel, gamma='scale').fit(X, y)
    plot_decision_boundary(model, X, y)
    
plt.tight_layout()
plt.show()

4. 效果对比图👇

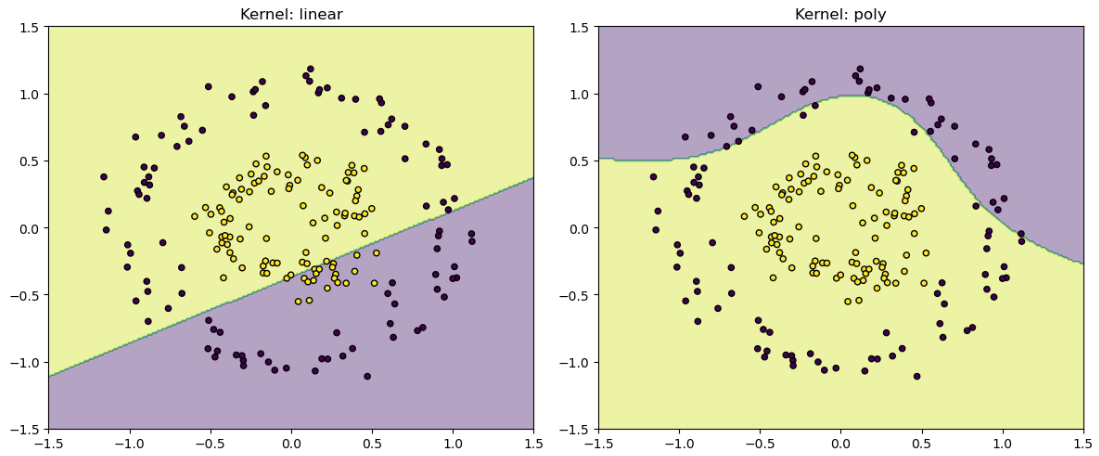
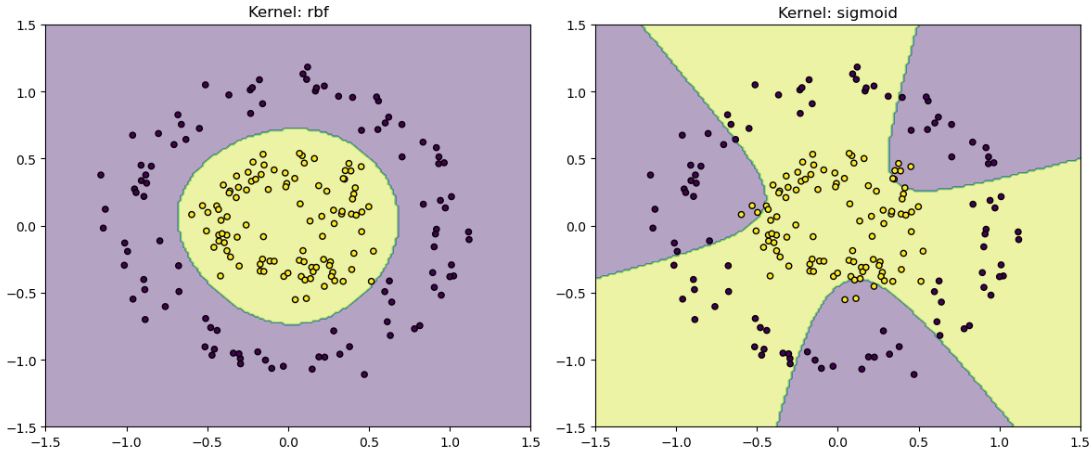
结果分析：

线性核：完全无法处理环形数据
多项式核：能部分拟合但边界不完美
RBF核：完美拟合环形边界
Sigmoid核：表现最差（符合预期）

五、参数调优技巧🛠️

1. RBF核参数调优

from sklearn.model_selection import GridSearchCV

param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [0.01, 0.1, 1, 'scale']
}

grid = GridSearchCV(SVC(kernel='rbf'), param_grid, cv=5)
grid.fit(X_train, y_train)
print("最佳参数:", grid.best_params_)

2. 多项式核参数建议

degree：通常2-5，超过3易过拟合
gamma：默认'scale'通常足够
coef0：控制高阶项影响，可从0开始尝试

六、常见问题解答❓

Q1: 核函数可以自定义吗？
A1: 可以！只需满足Mercer条件（核矩阵半正定）。示例：

def my_kernel(x, y):
    return np.dot(x, y.T) + np.sum(x**2) + np.sum(y**2)

model = SVC(kernel=my_kernel)

Q2: 如何判断数据是否需要非线性核？

A2: 先尝试线性核，若训练准确率远低于100%且测试集表现差，则考虑非线性核。

Q3: 为什么Sigmoid核很少使用？
A3: 理论上有吸引力，但实际效果常不如RBF核，且参数调节更敏感。

Q4：为什么RBF核是默认首选？
A4：RBF核映射到无限维空间，理论上可拟合任意复杂边界，且参数仅需调整γ和C。

Q5:如何避免SVM过拟合？

A5：优先降低γ值；减小C值增大间隔；增加正则化（如sklearn的class_weight='balanced'）

Q6：特征标准化对核函数重要吗？

A6：致命重要！ 特别是RBF核对特征尺度敏感，未标准化会导致某些维度主导计算

七、总结：核函数选择口诀🗣️

默认选择RBF核：除非有明确理由用其他核
线性核三板斧：高维稀疏数据+大规模数据+快速原型
多项式核当备胎：当RBF核参数难调时尝试
Sigmoid核慎用：除非你懂它在干什么

💡 温馨提示：核函数不是越复杂越好，适合数据的才是最好的！建议通过交叉验证实验确定最终方案。

欢迎在评论区分享你的核函数使用心得或遇到的问题！👇

拓展阅读：

人工智能基石：SVM支持向量机全解析（附Python实战）