决策树剪枝：让你的决策树更“聪明”_决策树什么时候需要剪枝-优快云博客

本文链接：https://blog.youkuaiyun.com/qiutesting/article/details/148608868

大家好，我是你们的技术分享小能手😎！今天咱们来聊聊决策树剪枝这个重要的话题。决策树在机器学习中可是个“明星选手”，但有时候它也会“长歪”，这时候剪枝就派上用场啦😏。

🤔什么是决策树剪枝？

决策树剪枝，简单来说，就是对决策树进行“修剪”，去掉一些不必要的分支，让决策树变得更简洁、更高效🌳。就像修剪树木一样，去掉多余的枝叶，让树木能更好地生长。

🧐决策树为什么需要剪枝？

决策树在构建过程中，如果不加限制，会一直生长下去，直到每个叶子节点都只包含一个样本或者达到最大深度。这样生成的决策树虽然对训练数据拟合得很好，但对新数据的预测能力却很差，这就是所谓的过拟合问题😱。

举个🌰：

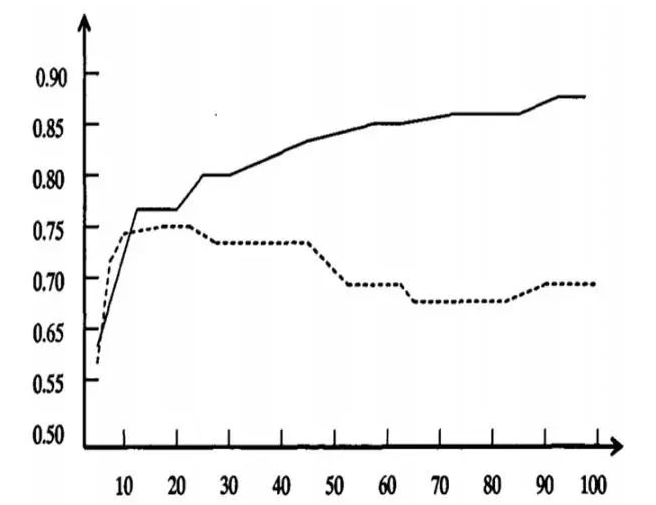
下图为决策树学习过程中的过度拟合。

横轴：决策树创建过程中树的结点总数。

纵轴：决策树的预测精度。

实线：决策树在训练集上的精度。

虚线：在独立测试集上测量出来的精度。

由图可以看出，随着树的增长，在训练集上的精度是单调上升的。然而在独立的测试样例上测出的精度先上升后下降。分析原因如下：

①噪声、样本冲突，即错误的样本数据。

②特征即属性不能完全作为分类标准。

③巧合的规律性，数据量不够大。

所以不剪枝的后果：

过拟合风险高：模型过度依赖训练数据中的噪声和异常值
模型复杂度高：树结构庞大，计算和存储开销大
泛化能力差：测试集表现显著低于训练集（例如训练精度100%，测试精度仅85%）

✨ 核心目标：通过剪枝降低方差（Variance），牺牲少量训练精度，换取更强的泛化能力，让决策树在新数据上也能有好的表现👍。

📋常用剪枝方法

🌱预剪枝（Pre-pruning）

原理

预剪枝是在决策树生成过程中，提前停止树的生长。当满足一定的条件时，就不再继续划分节点。

常用停止条件：

最大深度限制 (max_depth): 树的最大层数
最小样本分裂 (min_samples_split): 节点继续分裂所需的最小样本数
最小叶子样本 (min_samples_leaf): 叶节点最少样本数
信息增益阈值：划分带来的收益小于设定值

步骤

设置预剪枝条件：比如设置树的最大深度为 3，节点中样本的最小数量为 10，信息增益的最小阈值为 0.1。
构建决策树：在构建决策树的过程中，每次划分节点前，检查是否满足预剪枝条件。如果满足，就不再划分该节点，将其标记为叶子节点。
生成剪枝后的决策树：当所有节点都处理完毕后，就得到了预剪枝后的决策树。

✅ 优点：

显著降低训练时间和计算资源
减少过拟合风险

❌ 缺点：

贪心策略可能过早停止分裂（欠拟合风险）
对参数选择敏感

代码示例（使用 scikit-learn）

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# 加载数据
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 预剪枝参数设置
clf = DecisionTreeClassifier(
    max_depth=3,              # 最大深度
    min_samples_split=5,      # 最小分裂样本数
    min_samples_leaf=2,      # 叶节点最小样本
    random_state=42
)
clf.fit(X_train, y_train)

# 评估效果
print(f"训练集精度: {clf.score(X_train, y_train):.3f}")
print(f"测试集精度: {clf.score(X_test, y_test):.3f}")

# 可视化树
plt.figure(figsize=(12, 8))
plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

输出结果：

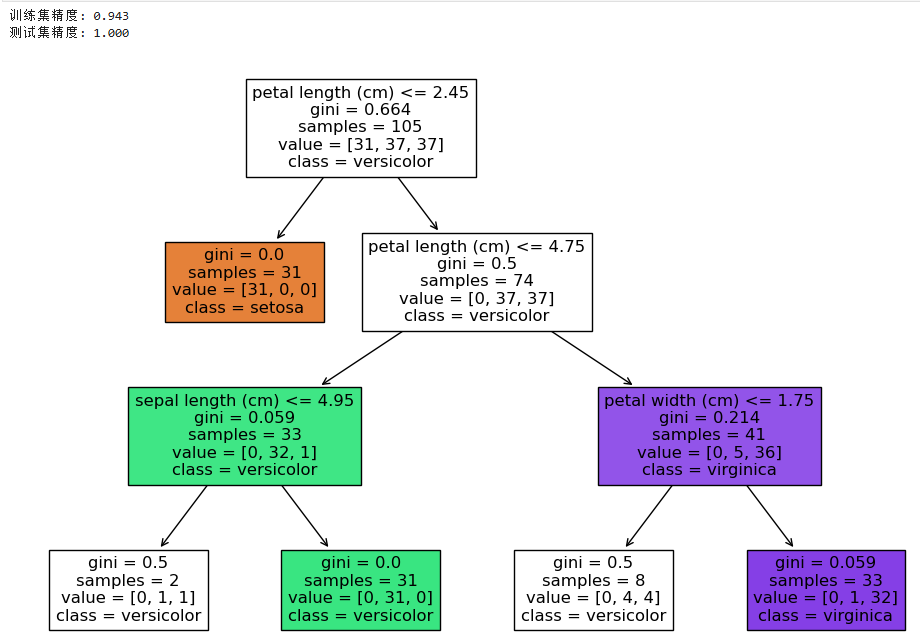
🌳后剪枝（Post-pruning）

原理

后剪枝是先生成一棵完整的决策树，然后从底部向上对非叶子节点进行考察，如果将该节点对应的子树替换为叶子节点能提高模型的泛化能力，就将该子树替换为叶子节点😃。

步骤

生成完整的决策树：不进行任何限制，生成一棵完整的决策树。
自底向上考察非叶子节点：从决策树的底部开始，依次考察每个非叶子节点。
判断是否剪枝：对于每个非叶子节点，计算将其对应的子树替换为叶子节点前后的模型性能（比如准确率）。如果替换后模型性能提高，就进行剪枝；否则，不进行剪枝。
生成剪枝后的决策树：当所有非叶子节点都考察完毕后，就得到了后剪枝后的决策树。

常用算法：
（ 1 ） REP- 错误率降低剪枝
（ 2 ） PEP- 悲观剪枝
（ 3 ） CCP- 代价复杂度剪枝
（ 4 ） MEP- 最小错误剪枝

✅ 优点：

保留更多有效分支，泛化性能通常优于预剪枝
欠拟合风险小

❌ 缺点：

需生成完整树，计算开销大
依赖验证集质量

代码示例（CCP剪枝方法）

# 生成CCP路径
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas = path.ccp_alphas

# 训练不同alpha的树
clfs = []
for ccp_alpha in ccp_alphas:
    tree = DecisionTreeClassifier(ccp_alpha=ccp_alpha, random_state=42)
    tree.fit(X_train, y_train)
    clfs.append(tree)

# 绘制精度变化
train_acc = [tree.score(X_train, y_train) for tree in clfs]
test_acc = [tree.score(X_test, y_test) for tree in clfs]

plt.figure(figsize=(10, 6))
plt.plot(ccp_alphas, train_acc, marker='o', label='训练集')
plt.plot(ccp_alphas, test_acc, marker='o', label='测试集')
plt.xlabel('Alpha参数')
plt.ylabel('精度')
plt.title('剪枝参数与模型精度关系')
plt.legend()
plt.show()

# 选择最优alpha（测试集精度最高）
best_alpha = ccp_alphas[test_acc.index(max(test_acc))]
best_tree = DecisionTreeClassifier(ccp_alpha=best_alpha, random_state=42)
best_tree.fit(X_train, y_train)

输出结果：

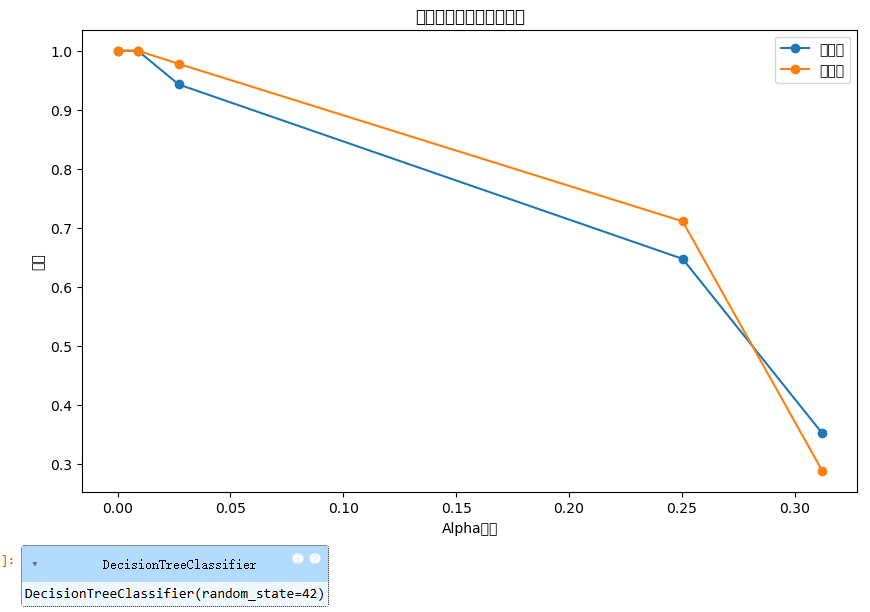
📊预剪枝和后剪枝的比较

特点	预剪枝	后剪枝
计算成本	较低，因为提前停止了树的生长	较高，需要先生成完整的决策树，然后进行剪枝
过拟合风险	较低，因为限制了树的生长	较低，因为通过自底向上的考察进行剪枝
欠拟合风险	较高，可能会过早停止树的生长，导致模型过于简单	较低，因为先生成完整的决策树，能更好地捕捉数据特征