算法导论第二章——插入排序和分治算法

2-1 插入排序

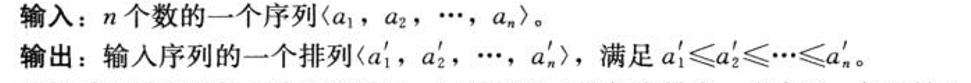
将序列的第一个作为参考，循环与下一个进行比较，若后者小于前者，则交换位置。

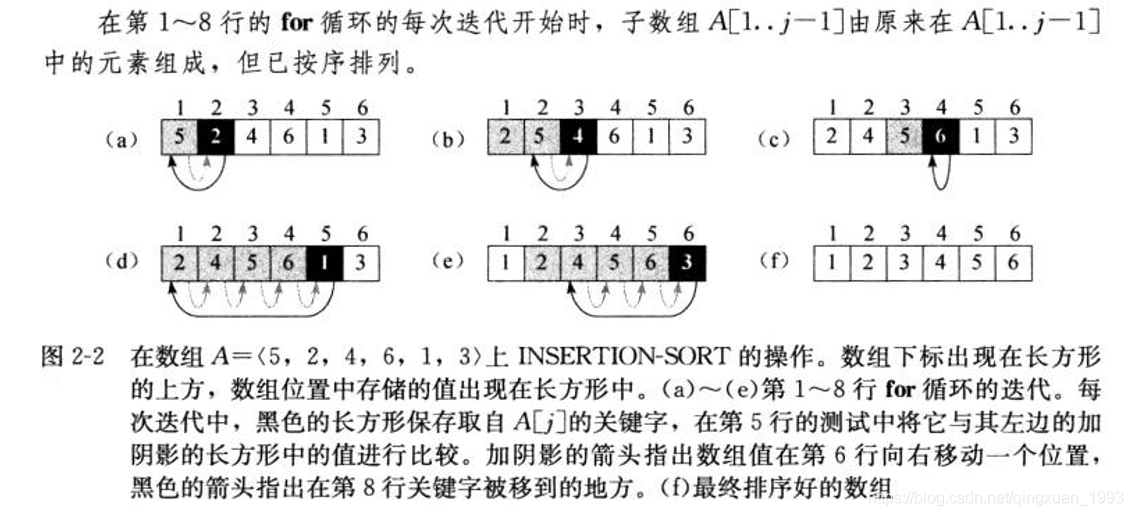
插入算法简单代码：

import sys

if __name__ == "__main__":
    n = list(map(int, sys.stdin.readline().strip().split(' ')))
    for i in range(1, len(n)):
        key = n[i]
        j = i-1
        while j>=0 and n[j]>key:
            n[j+1]=n[j]
            j=j-1
        n[j+1]=key
    print(n)

import sys
import numpy as np

if __name__ == "__main__":
    n1 = list(map(str, sys.stdin.readline().strip()))
    n1 = np.array(n1,dtype = np.int)
    n2 = list(map(str, sys.stdin.readline().strip()))
    n2 = np.array(n2,dtype = np.int)
    l = len(n1)
    carry = 0
    result = np.zeros(l+1,dtype = np.int)

    for i in range(0, l):
        j = l-i-1
        if n1[j] == 1 and n2[j] == 1:
            result[j+1] = 0 + carry
            carry = 1
        elif (n1[j] == 1 and n2[j] == 0) or (n1[j] == 0 and n2[j] == 1):
            result[j+1] = 1 + carry
            if result[j+1] == 2:
                carry = 1
                result[j+1] = 0
            else:
                carry = 0
        else:
            result[j+1] = 0 + carry
            carry = 0
    if carry == 1:
        result[0] = 1
    output = ''.join(str(i) for i in result)
    print(output)

这里需要注意的点有：
1、输入字符串转成数组，并以整数形式保存
2、创建常为n+1的0数组用来储存结果，同样整数形式。
3、进位carry的设置，何时进位，将情况梳理清楚。
4、输出时，将数组转为字符串的方法。

2-2 分析算法

通过伪代码，分析每一步需要执行的次数，并把他们相加。
通常只考虑最坏情况的运行时间。Θ(n)表示。
习题

1. Θ（n3）
2. 
   伪代码：
   for i in range(0, len(A)-1): n-1
   min = i n-2
   for j in range(i+1, len(A)): n(n-2)/2
   if A[j]<A[min]: n(n-2)/2
   min = j // 最好：0； 最坏：n(n-2)/2
   temp = A[i] n-2
   A[i] = A[min] n-2
   A[j] = temp n-2
   最好和最坏的情况都是Θ(n2)，算法不稳定

2-2-3：顺序查找的平均时间复杂度和最差时间复杂度都是Θ（n）

2-3 分治算法

许多有用的算法在结构上是递归的：为了解决一个给定的问题，算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。

这些算法典型的遵循分治法的思想，将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

归并排序

算法思想：
归并过程：将两组已经分别排好序的数组，合并成一个排好序的数组。依次比较两个数组最小的数，将小的添加到输出数组中，比较n次后可以得到最终结果。
伪代码：

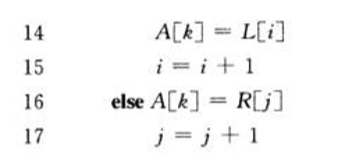
递归过程：
输入一个乱序的数组，将其依次分解，直到每组只有一个元素，那么这组就是有序的了，再两两进行归并过程。

伪代码：

分析分治算法

归并排序的复杂度分析
n个数最坏情况：
n>1
分解：计算中间位置， 需要常量时间D(n)=Θ(1)
解决：递归地求解两个规模为n/2的子问题，将贡献2T(n/2)的运行时间
合并：在一个具有n个元素的子数组上合并需要Θ(n)的时间。
T(n)=2T(n/2)+Θ(n)

递归树：
总代价为：cnlgn+cn，忽略常数项和低阶项
即为Θ(nlgn)

递归排序代码（没有哨兵习题2-3-2）：

import sys

def merge(A,p,q,r):
    n1 = q-p+1
    n2 = r-q
    L=[0]*n1
    R=[0]*n2
    for i in range(0,n1):
        L[i] = A[p+i]
    for j in range(0,n2):
        R[j] = A[q+1+j]
    i = 0
    j = 0
    k = p
    while i<n1 and j<n2:
        if L[i]<=R[j]:
            A[k]=L[i]
            i = i+1
        else:
            A[k]=R[j]
            j = j+1
        k = k+1
 #当把一个子数组完全填入A中后，剩下的子数组中如果还有元素，那么将其复制到A中，因为都是最大的，按顺序复制就行了。       
    while i < n1:
        A[k] = L[i]
        i += 1
        k += 1

        # 拷贝 R[] 的保留元素
    while j < n2:
        A[k] = R[j]
        j += 1
        k += 1



def mergesort(A,p,r):
    if p<r:
        q=int((p+r-1)/2)
        mergesort(A,p,q)
        mergesort(A,q+1,r)
        merge(A,p,q,r)


if __name__ == "__main__":
    A = list(map(int, sys.stdin.readline().strip().split(' ')))
    mergesort(A,0,len(A)-1)
    print(A)

2-3-4
递归的插入排序：

import sys

def insert(A,r):
    key = A[r]
    # 不用for 是因为需要判断条件才决定是否循环。
    # for i in range(0,r):
    #     if key>A[p-i]:
    #         for j in range(0,i):
    #             A[r-j]=A[r-j-1]
    #         A[p-i+1] = key
    #         break
    #     else:
    #         if i == p:
    #             for k in range(0,r):
    #                 A[p-k+1] = A[p-k]
    #             A[0]=key
    i = r
    while i>0 and key<A[i-1]:
        A[i] = A[i-1]
        A[i-1] = key
        i = i-1



def mergesort(A,r):
    if r>0:
        mergesort(A,r-1)
        insert(A,r)


if __name__ == "__main__":
    A = list(map(int, sys.stdin.readline().strip().split(' ')))
    mergesort(A,len(A)-1)
    print(A)

分解：Θ(1)
解决：T（n-1）
合并：Θ（n）

最终最坏的时间复杂度为：Θ(n2)

2.3-5
二分查找递归写法：

import sys

index = 0

def halffind(A,p,r,v):
    global index
    if index == 0:
        q = int((r+p+1)/2)
        if q<=r and q>=p:
            if v>A[q] :
                halffind(A,q+1,r,v)
            elif v<A[q]:
                halffind(A,p,q-1,v)
            else:
                index = q
        else:
            index = None

if __name__ == "__main__":
    A = list(map(int, sys.stdin.readline().strip().split(' ')))
    v = int(sys.stdin.readline().strip())
    halffind(A, 0, len(A)-1, v)
    if index == None:
        print('null')
    else:
        print(index)

return 版不用全局变量也少了很多判断，原来保留结果的递归是这样用的呀。继续多学习呀：

import sys

# index = 0

def halffind(A,p,r,v):

    q = int((r+p+1)/2)
    if q<=r and q>=p:
        if v>A[q] :
            return halffind(A,q+1,r,v)
        elif v<A[q]:
            return halffind(A,p,q-1,v)
        else:
            return q
    else:
        return None

if __name__ == "__main__":
    A = list(map(int, sys.stdin.readline().strip().split(' ')))
    v = int(sys.stdin.readline().strip())
    index = halffind(A, 0, len(A)-1, v)
    if index == None:
        print('null')
    else:
        print(index)

只有递归过程是T(n/2), 其他都是Θ（1），所以时间复杂度为Θ(lgn)

2.3-6 转载：https://www.cnblogs.com/heyuquan/p/insert-sort.html

算法复杂度

1. 时间复杂度：O(n^2)
   二分查找插入位置，因为不是查找相等值，而是基于比较查插入合适的位置，所以必须查到最后一个元素才知道插入位置。
   二分查找最坏时间复杂度：当2^X>=n时，查询结束，所以查询的次数就为x，而x等于log2n（以2为底，n的对数）。即O(log2n)。
   所以，二分查找排序比较次数为：x=log2n

二分查找插入排序耗时的操作有：比较 + 后移赋值。时间复杂度如下：

1. 最好情况：查找的位置是有序区的最后一位后面一位，则无须进行后移赋值操作，其比较次数为：log2n 。即O(log2n)
2. 最坏情况：查找的位置是有序区的第一个位置，则需要的比较次数为：log2n，需要的赋值操作次数为n(n-1)/2加上 (n-1) 次。即O(n^2)
3. 渐进时间复杂度（平均时间复杂度）：O(n^2)

2.空间复杂度：O(1)
从实现原理可知，二分查找插入排序是在原输入数组上进行后移赋值操作的（称“就地排序”），所需开辟的辅助空间跟输入数组规模无关，所以空间复杂度为：O(1)

(三)稳定性
二分查找排序是稳定的，不会改变相同元素的相对顺序。