回文自动机学习笔记

最新推荐文章于 2025-07-13 20:03:16 发布

原创最新推荐文章于 2025-07-13 20:03:16 发布 · 211 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#回文自动机 #回文树

字符串专栏收录该内容

12 篇文章

订阅专栏

回文自动机学习笔记

由两棵子树构成

一棵节点编号为0，子树是长度为偶数的回文串
一棵节点编号为1，子树是长度为奇数的回文串

回文自动机

奇偶回文串处理

$l e n [0] = 0, l e n [1] = - 1$ 使得在 $1$ 号子树下的字符串长度 $- 1$

$f a i l [0] = 1$ 使得字符串最终能跳到 $- 1$ ，即本身为回文串

$f a i l [1] = 0$ 使得本身为回文串的情况，最小真后缀回文串为0成立

回文树节点

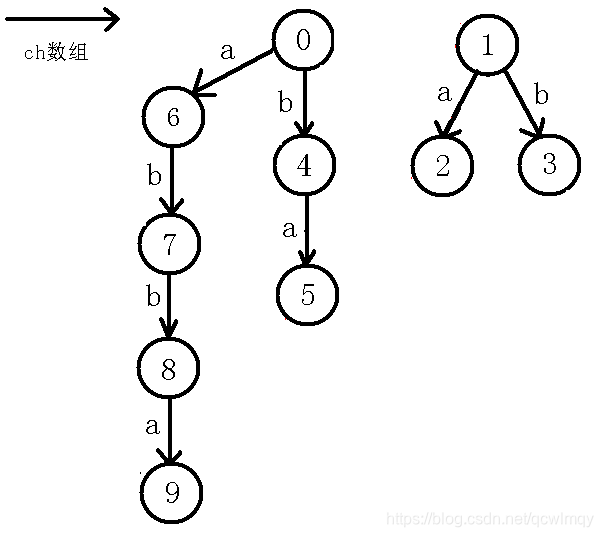
对于 $0$ 号子树，路径上的字母表示回文串后半段
以 $5$ 号节点为例，表示的是baab
对于 $1$ 号子树，路径上的字母表示回文串后半段（包括中间字符）
以 $2$ 号节点为例，表示的是 $a$

此图片为 $a b b a a b b a$ 的回文树

建树

$i n [0] =^{'}^{'}$ ，为必定不相同的字符

$f a i l []$ ：表示当前回文串的最长真后缀回文串

找到最新节点 $l a s t$ ，
寻找 $l a s t$ 代表回文串的前一个点： $i n [i - l e n [l a s t] - 1]$
与当前节点（ $i n [i]$ ）比较，若相当于在原回文串两边加上一个字符ch
创建新的节点且 $l e n [t r e e [l a s t] [c h]] = l e n [l a s t] + 2$
若当前回文串不匹配，跳 $f a i l$ 指针寻找最长真后缀回文子串是否匹配
最终至少会跳到 $f a i l [0] = = - 1$ ，字符本身必定为回文串

$f a i l$ 指针建立

寻找一个回文串的最长真后缀回文子串

相当于寻找 $l a s t$ 回文串的最长真后缀回文子串的匹配回文串

定义一个新变量 $j$ 跳到 $f a i l [l a s t]$
如建树一样寻找匹配回文串即可
对于以自己为回文串的回文串 $f a i l [1] = 0$ ，不然至少找到本身

代码

$i n []$ ：字符串

$t r e e [n] [c h]$ ：字典树

$f a i l []$ ： $f a i l$ 指针跳转到当前回文串的** 最长真后缀回文串**

$l e n []$ ：当前回文串的长度

初始化

scanf("%s", in + 1); in[0] = '#';
//第一个为不同字符
fail[0] = 1; fail[1] = 0;
//保证最终跳到本身
len[0] = 0; len[1] = -1;
//易处理处理
last = 0;
//last最新节点置0
num = 1;
//字典树编号，已有2个节点：0，1

建树

for (int i = 1; i <= n; i++) {
	while (in[i - len[last] - 1] != in[i]) last = fail[last];
	//跳到第一个匹配的串
	if (!tree[last][in[i] - 'a']) {//若改字符串不存在
		len[++num] = len[last] + 2;//新的回文串为原回文串+2
		int j = fail[last];//当前串的最长真后缀回文串
		while (in[i - len[j] - 1] != in[i]) j = fail[j];
		//最长真后缀回文串的第一个匹配串
		fail[num] = tree[j][in[i] - 'a'];
		tree[last][in[i] - 'a'] = num;
		//字典树编号
	}
	last = tree[last][in[i] - 'a'];
	//更新last
}