灵敏度函数

灵敏度

灵敏度函数是描述了系统输出对输入或系统参数变化的响应程度，一般来说定义为：
$$S=\frac{dY(s)/Y(s)}{dX(s)/X(s)}\text{\hspace{1em}(1)}$$其中，$Y(s)$是系统输出，$X(s)$是系统参数。

开环系统灵敏度

对于开环系统，只存在前向路径，没有反馈回路。则系统的传递函数可表示为：
$$G(s)=\frac{Y(s)}{R(s)}$$根据灵敏度公式(1)，开环系统灵敏度为：$$S(s)=\frac{dY(s)/Y(s)}{dG(s)/G(s)}=1$$可以看出开环控制系统对于摄动的作用毫无抑制能力，任何摄动产生的结果会完全影响到系统的输出。

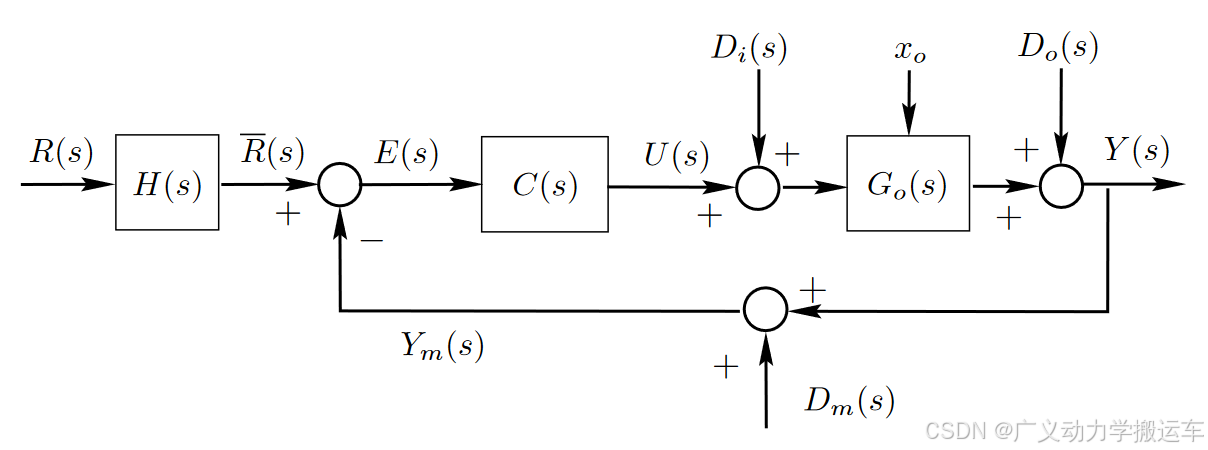
闭环系统灵敏度

众所周知，闭环系统传递函数为
$$T(s)=\frac{G(s)}{1+G(s)H(s)}=G(s)(1+G(s)H(s){)}^{-1}$$则 $$\Delta T=\frac{\Delta G}{(1+G(s)H(s){)}^2}$$代入(1)得$$S=\frac{\Delta T/T}{\Delta G/G}=\frac{1}{1+G(s)H(s)}$$

未完待续…