深度学习入门（五）：神经网络的学习之数值微分和梯度

数值微分

梯度法使用梯度的信息决定前进的方向。而首先要明白导数的作用。
导数定义这里不再赘述，这里主要强调数值微分的概念。
利用微小的差分求导数的过程称为数值微分（numerical differentiation）。而基于数学式的推导求导数的过程，则用“解析性”（analytic）一词，称为“解析性求解”或者“解析性求导”
首先，在计算程序中会产生微小值导致的舍入误差。
其次，数值微分和解析性求导相比，会产生误差。这是由导数定义$f^{\prime }(a)={\lim }_{h\to 0}\frac{f(a+h)-f(a)}{h}$中的$h$导致的，因为$h$不可能无限接近于0。
为了减小误差，可以计算函数在$(x+h)$和$(x-h)$之间的差分。这种计算方法称为中心差分。
$(x+h)$和$x$之间的差分称为前向差分。

实例

这个导数在$x=5$和$x=10$两处的“真的导数”分别为0.2和0.3，而计算差分值为0.19999和0.29999，虽然在严格意义上不相等，但是误差非常小，小到可以认为它们是相等的。

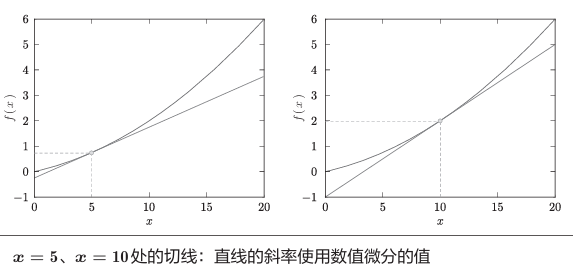
当然，以上概念全部可以扩展到多元函数的偏导数上。
有多个变量的函数的导数称为偏导数。以函数$f(x_0,x_1)=x_0^2+x_1^2$为例，其中两个变量的公式可以表示为$\frac{\partial f}{\partial x_0}$和$\frac{\partial f}{\partial x_1}$。
偏导数和单变量的导数一样，都是求某个地方的斜率。不过，偏导数需要将多个变量中的某一个变量定为目标变量，并将其他变量固定为某个值。

梯度

像$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})$这样的由全部变量的偏导数汇总而来的向量称为梯度。梯度的计算方法不再赘述。

梯度指示的方向是各点处的函数值减小最多的方向。

梯度法

机器学习的主要任务是在学习时寻找最优参数。同样地，神经网络也必须在学习时找到最优参数（权重和偏置）。即损失函数取最小值的参数。
一般而言，损失函数很复杂，参数空间庞大，不知道在何处可以取最小值，梯度法就是解决这个问题。
需要注意的是，梯度表示的是各点处的函数值减小最多的方向。因此，无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际上，在复杂的函数中，梯度指示的方向基本上都不是函数值最小处。虽然梯度方向不一定指向最小值，但是能最大限度减小函数的值，因此可以作为线索。
函数的极小值、最小值以及被称为鞍点（saddle point）的地方，梯度为0。
梯度法就是指函数的取值从当前位置沿着梯度方向前进一定距离，然后重新求梯度，再沿着新梯度方向前进，如此反复，不断前进，可以做到函数值逐渐减小。
梯度法是解决机器学习中最优化问题的常用方法，特别是在神经网络的学习中经常被使用。
严格地讲，寻找最小值的梯度法称为梯度下降法（gradient descent method），寻找最大值的梯度法称为梯度上升法（gradient ascent method）。
数学式如下：

$\eta$表示更新量，在神经网络的学习中称为学习率。学习率决定一次学习中，应该学习多少，以及在多大程度上更新参数。学习率需要事先确定为某个值，比如0.01或0.001。一般而言，这个值过大或过小，都无法抵达一个“好的位置”。在神经网络的学习中，一般会一边改变学习率的值，一边确认学习是否正确进行了。
学习率过大的话，会发散成一个很大的值；反过来，学习率过小的话，基本上没怎么更新就结束了。也就是说，设定合适的学习率是一个很重要的问题。
像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数。超参数是人工设定的，一般而言要尝试多个值。

神经网络的梯度

神经网络的学习也要求梯度。这里所说的梯度是指损失函数关于权重参数的梯度。