深度学习入门（六）：学习算法的实现

神经网络的学习步骤

• 前提：
  神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为“学习”。
• 步骤1（mini-batch）：
  从训练数据中随机选出一部分数据称为mini-batch，目的是减小mini-batch的损失函数的值。
• 步骤2（计算梯度）：
  为了减小mini-batch的损失函数的值，需要求出各个权重参数的梯度。梯度表示损失函数的值。
• 步骤3（更新参数）：
  将权重参数沿梯度方向进行微小更新。
• 步骤4（重复）：
  重复上述步骤1、2、3。

神经网络的学习按照上面4个步骤进行。这个方法通过梯度下降法更新参数，不过因为这里使用的数据是随机选择的mini batch数据，所以又称为随机梯度下降法。“随机”特指“随机选择的”的意思。
随机梯度下降法一般由一个名为SGD的函数来实现，SGD来源于首字母。

2层神经网络

由一个名为TwoLayerNet的类实现。

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
    
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        
        return y
        
    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)
        
        return cross_entropy_error(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}
        
        batch_num = x.shape[0]
        
        # forward
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        
        # backward
        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)
        
        da1 = np.dot(dy, W2.T)
        dz1 = sigmoid_grad(a1) * da1
        grads['W1'] = np.dot(x.T, dz1)
        grads['b1'] = np.sum(dz1, axis=0)

        return grads

以下是重要的变量和方法：


params保存了权重参数，grads保存了各个参数的梯度。
再来看初始化函数，def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01)中，输入参数依次表示输入层的神经元数、隐藏层的神经元数、输出层的神经元数。
此外，这个初始化方法会对权重参数进行初始化（这里设置为了0.01）。权重使用符合高斯分布的随机数进行初始化，偏置使用0进行初始化。

mini-batch实现

神经网络的学习的实现使用的是mini-batch学习。
代码如下：

import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000  # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 计算梯度
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch)
    
    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

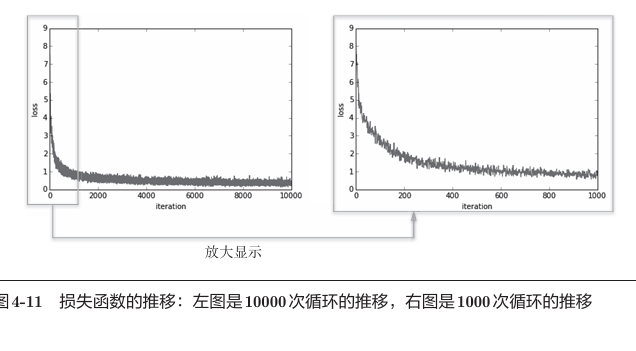
随着学习的进行，损失函数的值在不断减小。这是学习正常进行的信号，表示神经网络的权重参数在逐渐拟合数据。也就是说，神经网络正在逐渐向最优参数靠近。

基于测试数据的评价

由前文可知，反复学习可以使损失函数值逐渐减小。但是严格来说，减少的是“对训练数据的某个mini-batch的损失函数”的值。光看这个结果还不能说明在其他数据集上也一定能有同等程度的表现。
神经网络的学习必须确认是否能够正确识别训练数据以外的数据，即确认是否会过拟合。因此，要评价神经网络的泛化能力，就必须使用不包含在训练数据中的数据。
epoch是一个单位。一个epoch表示学习中所有训练数据均被使用过一次时的更新次数。

train_acc_list = []
test_acc_list = []
#平均每个epoch的重复次数
iter_per_epoch = max(train_size / batch_size, 1)

 #计算每个epoch的识别精度
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

每经过一个epoch，就对所有的训练数据和测试数据计算识别精度，并记录结果。之所以要计算每一个epoch的识别精度，是因为如果在for语句的循环中一直计算识别精度，会花费太多时间。
并且，也没有必要那么频繁地记录识别精度，只要从大方向上大致把握识别精度的推移就可以了。

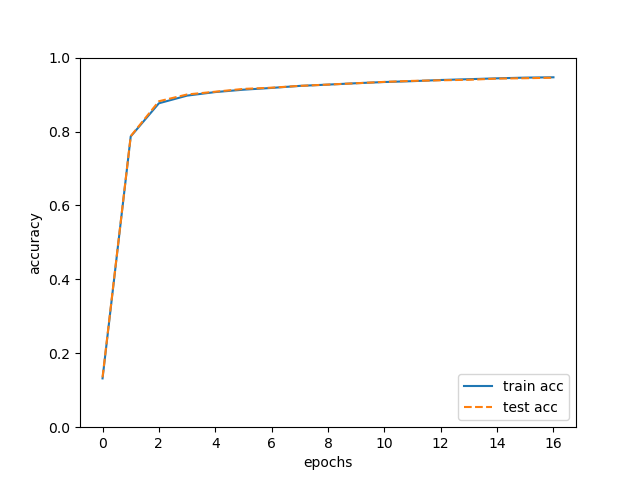
随着学习的进行，我们发现使用训练数据和测试数据评价的识别精度都提高了，并且，这两个识别精度基本上没有差异。因此，可以说这次的学习中没有发生过拟合的现象。