深度学习入门（四）：神经网络的学习过程之损失函数

这里的学习，指的是从训练数据中自动获取最优权重参数的过程。

从数据中学习

这本就是神经网络的特征之一。这句话的意思是指由数据自动决定权重参数的值，从而超越人工处理。在深度学习中，参数的数量远超人工可处理的范围。

数据驱动

数据是机器学习的核心，机器学习方法极力避免人为介入，尝试从数据中发现答案。神经网络或深度学习则更加强化了这一点。
例如识别数字，人能分辩数字，但是说不出规律，更何况机器呢？因此需要通过海量的数据来驱动这个识别学习的过程，一种方案是特征量，从图像中提取特征量，再用机器学习技术学习这些特征量的模式。
特征量是指可以从输入端中准确提取本质数据（重要的数据）的转换器，图像的特征量通常表现为向量的形式。在计算机视觉领域，常用的特征量包括SIFT、SURF、和HOG等。
使用特征量将图像数据转换为向量，抓住关键，然后用机器学习中的SVM、KNN等分类器进行学习。
虽然收集数据找出规律性能减轻人的负担，但是图像转换为向量时使用的特征值仍然是由人设计的。对于不同的问题要使用合适的特征量（必须设计专门的特征量），才能得到好结果。即需要针对不同问题人工考虑合适的特征量。

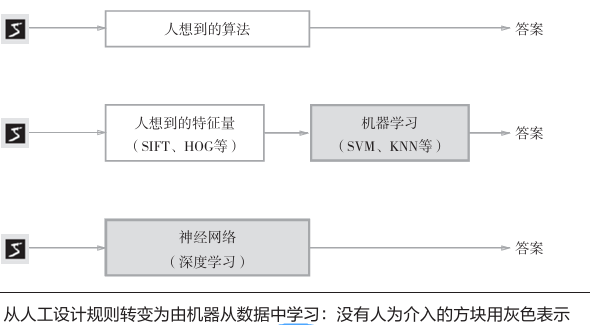
神经网络的一大优点在于所有问题可以用同样的流程解决。与待处理的问题无关，神经网络可以将数据直接作为原始数据，进行“端对端”的学习。

训练数据和测试数据

机器学习中一般将数据分为训练数据和测试数据两部分来进行学习和实验等。首先，使用训练数据进行学习，寻找最优参数；然后使用测试数据评价训练得到的模型的实际能力。

为什么需要将数据分为训练数据和测试数据呢？
因为我们追求的是模型的泛化能力。为了正确评价模型的泛化能力，就必须划分训练数据和测试数据。另外，训练数据也可以称为监督数据。

泛化能力
泛化能力是指处理未被观察过的数据（不包含在训练数据中的数据）的能力。获得泛化能力是机器学习的最终目标！例如：还是数字识别，最终可导要被用在读取数字编码的系统上，如果不能做到识别任一目标，只能识别训练结果，那有可能只是识别了个人特征。
因此，仅用一个数据集去学习和评价参数，是无法进行正确评价的。（裁判不能自己下场打比赛）

只对某个数据集过度拟合的状态称为过拟合，避免过拟合也是机器学习的一个重要课题。

损失函数

神经网络的学习通过某个指标表达现在的状态。然后以这个指标为基准寻找最优权重参数。这个指标被称为损失函数（loss function），可以使用任何函数，但是一般用均分误差和交叉熵误差。

损失函数是表示神经网络性能的“恶劣程度”的指标，即当前的神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。

均方误差

损失函数中最有名的就是均方误差了，公式如下：
$$E=\frac{1}{2}\sum _k(y_k-t_k{)}^2$$
其中$y_k$是神经网络的输出，$t_K$表示监督数据，$K$表示数据的维度。
均方误差会计算神经网络的输出和正确解监督数据的各个元素之差的平方，再求总和。

正确解标签的索引为1，其他均为0，这种表示方法称为one-hot表示。

交叉熵误差

除均方误差外，交叉熵误差也经常被用作损失函数。
$$E=-\sum _k{t}_k\log y_k$$
这里的$t_k$表示正确解标签。并且，$t_k$也是one-hot表示。因此，公式中实际上只计算对应正确解标签的输出的自然对数。交叉熵误差的值是由正确解标签所对应的输出结果决定的。
由于对数函数的特性，x等于1，y等于0；随着x向0靠近，y逐渐变小。因此正确解标签对应的输出越大，式的值越接近0。此外，如果正确解标签对应的输出较小，则式的值较大。

mini-batch学习

所谓使用训练数据学习，就是针对训练数据计算损失函数的值，找出尽可能使该值小的参数。
即损失函数与训练结果优秀程度成反相关。
计算损失函数，必须把所有训练数据作为对象。即最后的指标是所有训练数据的所有损失函数之和。最后，还要除以N进行平均化，获得与数量无关的统一指标。
另外，若一个数据集数据量太大，则计算时间也相应会变大，甚至到无法计算的程度。因此可以从全部数据中选取一部分，作为“近似”（或者说，样本）。神经网络的学习也是从训练数据中随机选取一批数据（称为mini-batch，小批量），然后对每个mini-batch进行学习。这就是mini-batch学习。

为何要设定损失函数

为何要导入损失函数，而不是将正面、积极的指标作为参考指标？
这个问题的回答需要使用“导数”在神经网络学习中的作用来理解。

确切来说，这里的导数指的是梯度

导数值为负，通过使权重参数正向改变，可以减小损失函数的值；导数值为正，通过使权重参数向负方向改变，可以减小损失函数的值。当导数值为0，怎么都无法改变，此时权重更新会停在此处。

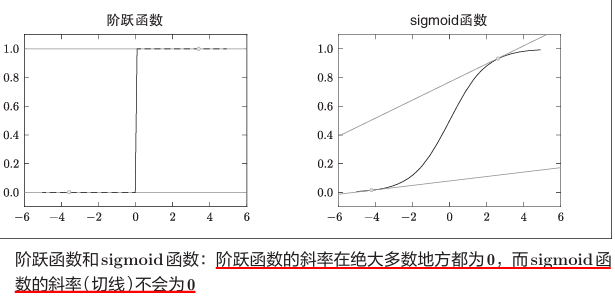
之所以不能用识别精度作为指标，是因为这样一来绝大多数地方的导数都会变为0，导致参数无法更新。
识别精度（如分类准确率）是一个​​离散的、不连续的指标​​。例如，假设当前模型在100个样本中正确分类32个，准确率为32%。若通过微调参数使正确分类数增加到33个，准确率会突变为33%，但这种变化是​​跳跃的、非连续的​​。
这种特性会使得导数几乎全部为0，参数的微小变化可能不会引起识别精度的任何变化（例如从32%到32%），此时导数（梯度）为0，无法指导参数更新。而如果是损失函数作为指标，则同等条件下可以表示为0.92543这样的值，稍微改变参数也会变为0.93432，发生连续变化。

损失函数通常基于模型输出的概率分布（如softmax输出），通过最大似然估计优化参数。例如，交叉熵损失通过消除激活函数（如sigmoid）的饱和效应（sigmoid函数的导数在任何地方都不为0），使梯度在错误预测时保持较大值，加速参数更新。