sklearn-1监督学习(1）

1 分类与回归

监督学习主要有两种问题：分类与回归

分类：对输入数据分类，输出是分类的结果（离散）

回归：对连续数据做出预测，输出为预测值（连续，如一条绳子让你看绳子预测它有多长）

2 一些样本数据

2.1 二分类数据集

 

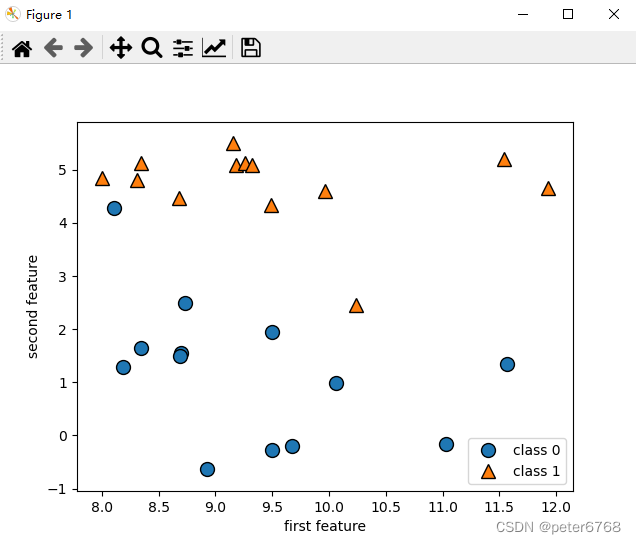
>>> x,y = mg.datasets.make_forge()
>>> mglearn.discrete_scatter(x[:,0],x[:,1],y)
[<matplotlib.lines.Line2D object at 0x000001AA35211880>, <matplotlib.lines.Line2D object at 0x000001AA332EB070>]
>>> plt.legent(['class 0', 'class 1'], loc=4)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: module 'matplotlib.pyplot' has no attribute 'legent'
>>> plt.legend(['class 0', 'class 1'], loc=4)
<matplotlib.legend.Legend object at 0x000001AA32F3C940>
>>> plt.xlabel('first feature')
Text(0.5, 0, 'first feature')
>>> plt.ylabel('second feature')
Text(0, 0.5, 'second feature')
>>> plt.show()

2.2 回归数据集

 

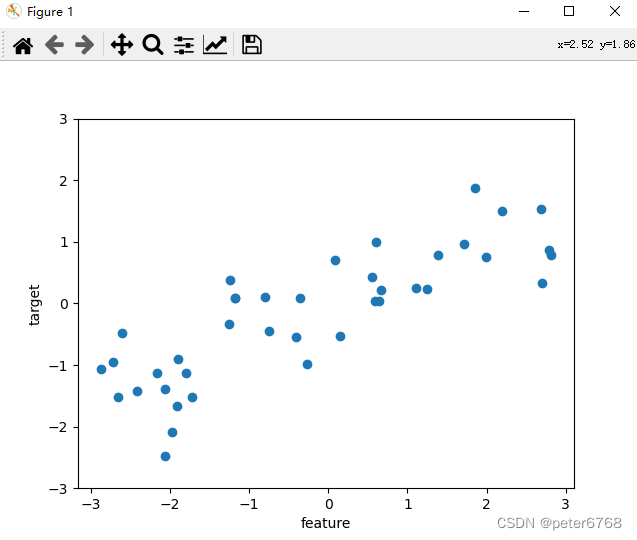
>>> x, y = mg.datasets.make_wave(n_samples=40)
>>> plt.plot(x, y, 'o')
[<matplotlib.lines.Line2D object at 0x000001AA334B7DF0>]
>>> plt.ylim(-3,3)
(-3.0, 3.0)
>>> ply.xlabel('feature')
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'ply' is not defined
>>> plt.xlabel('feature')
Text(0.5, 0, 'feature')
>>> plt.ylabel('target')
Text(0, 0.5, 'target')
>>> plt.show()

2.3 乳腺癌数据集

3 k近邻算法

3.1 k近邻分类

 

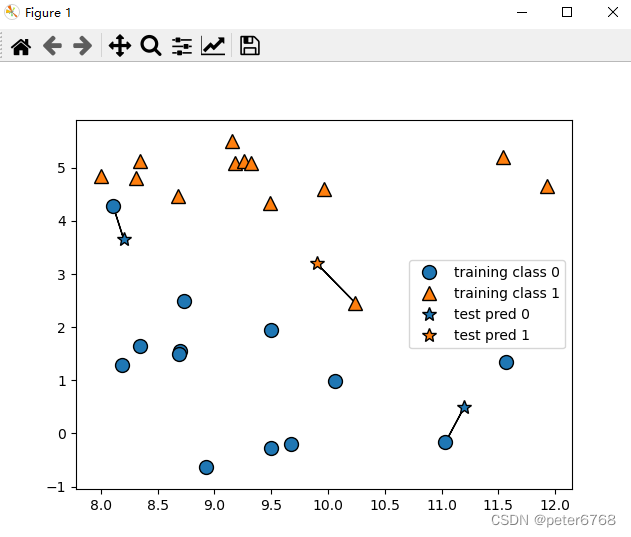
 通过scikit-learn使用k近邻算法

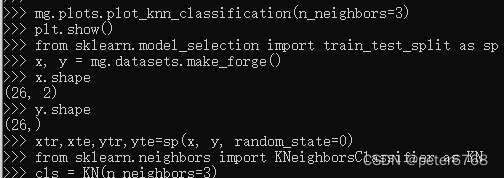
 训练模型

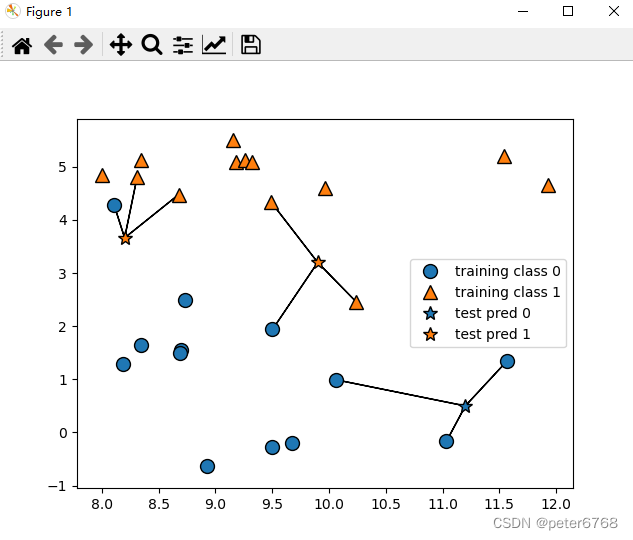
 预测模型

1 查看二分类问题决策边界 使用forge数据集

 

 

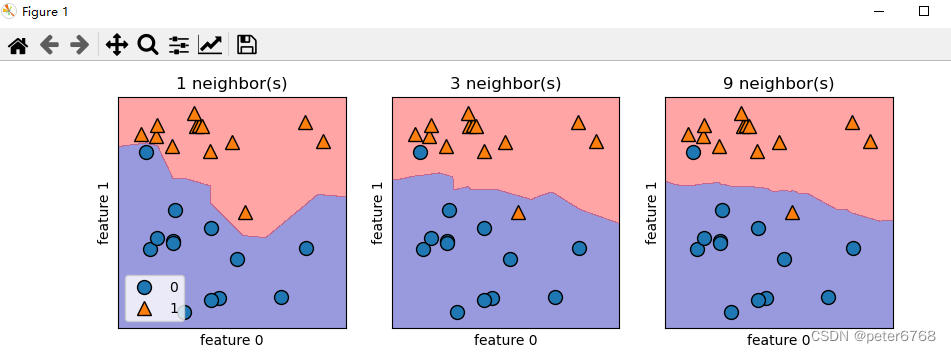
 2 看下乳腺癌数据里模型泛化能力准确性

 

 

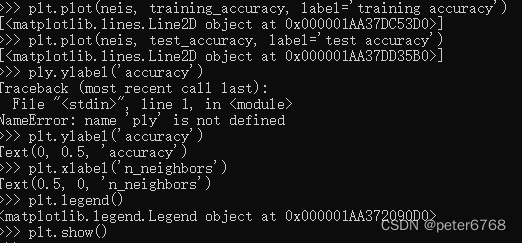
3.2 k临近算法回归

使用wave数据集，先直观感受下k临近

 

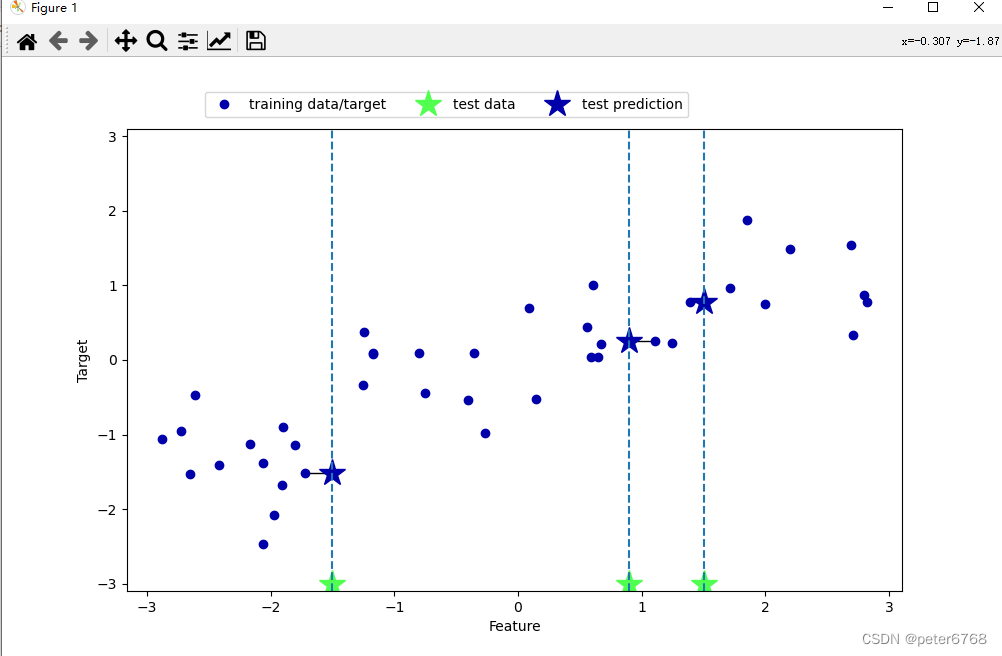
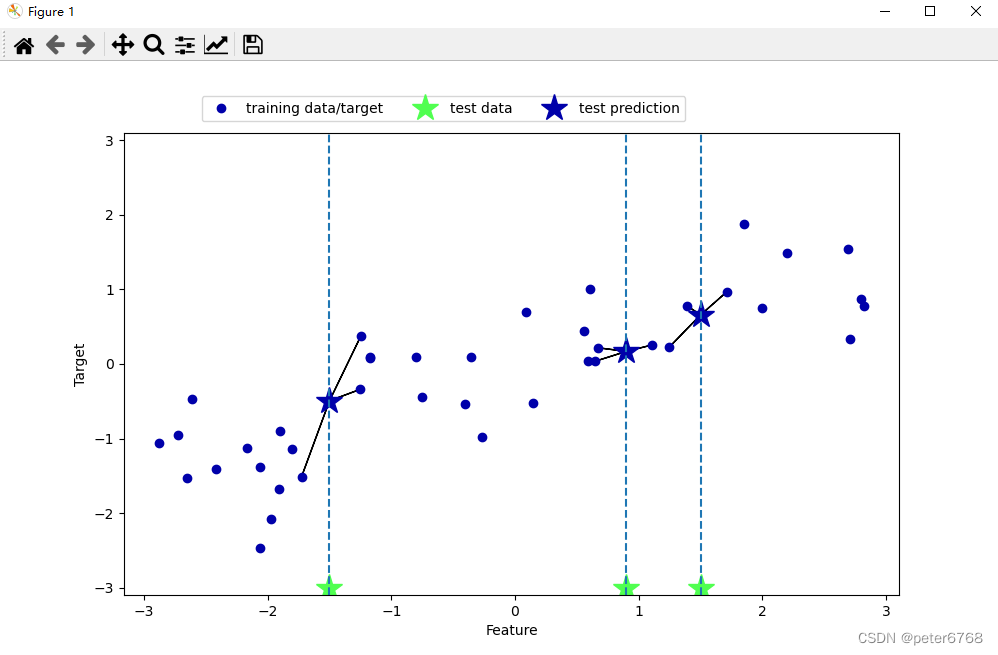
 校验数据泛化可信度

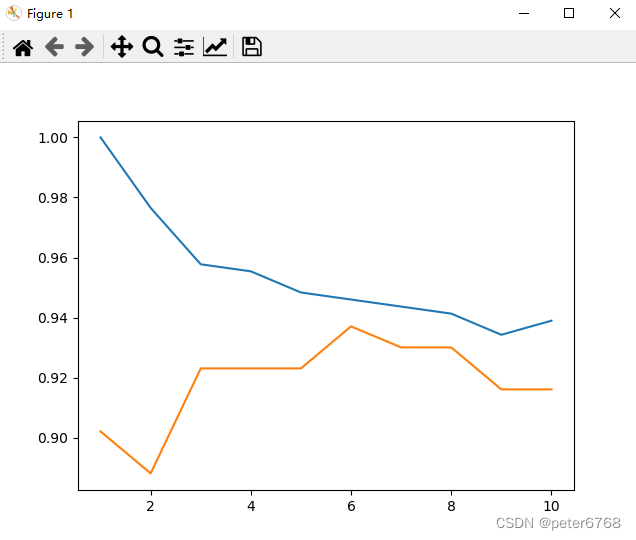
 看下邻居数不同时拟合准确度

 

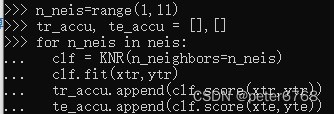
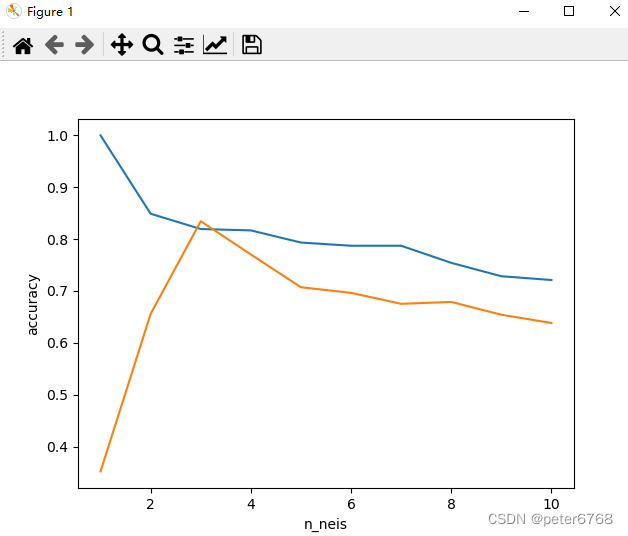
发现邻居为3时 拟合测试集和数据集精度接近

对于回归问题，knn对象的score方法返回准确度为差值的平方，值为0表示常数关系，值为1表示完美拟合

对wave数据集查看不同neighbors的拟合结果

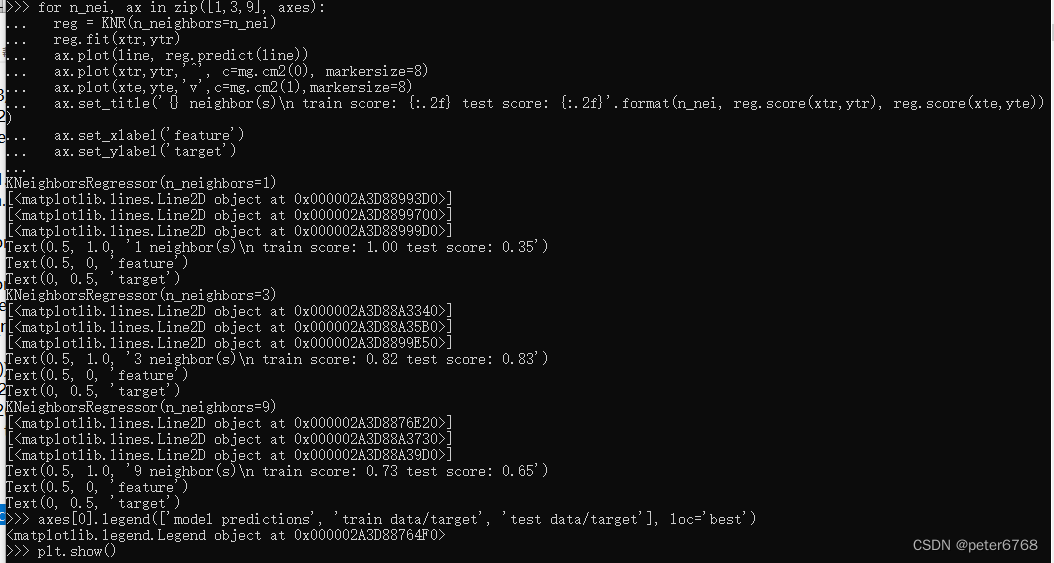
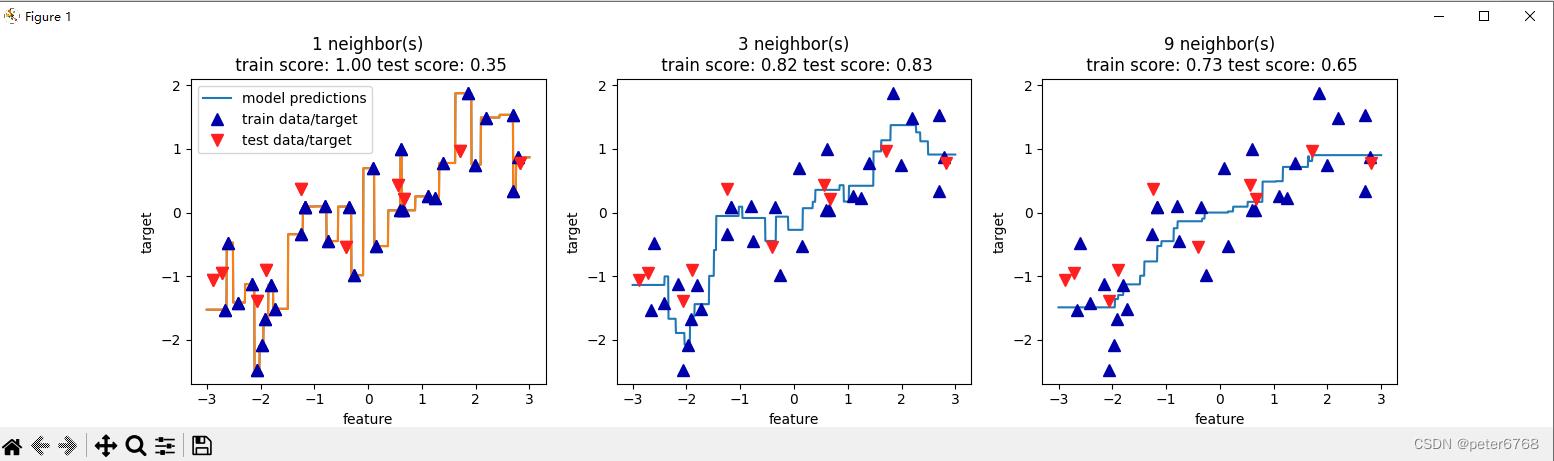
3.3 优缺点

优点

knn模型易理解，不需要过多调节即可获取不错的性能，是一种较好的基础方法

缺点

数据量大时，或特征值很多时，速度较慢，效果会打折，对稀疏矩阵来说性能会很低，此时数据预处理很重要

4 线性模型

线性回归通用公式

4.1 回归线性模型

即将数据点用一条直线拟合，方法直接对wave数据进行拟合

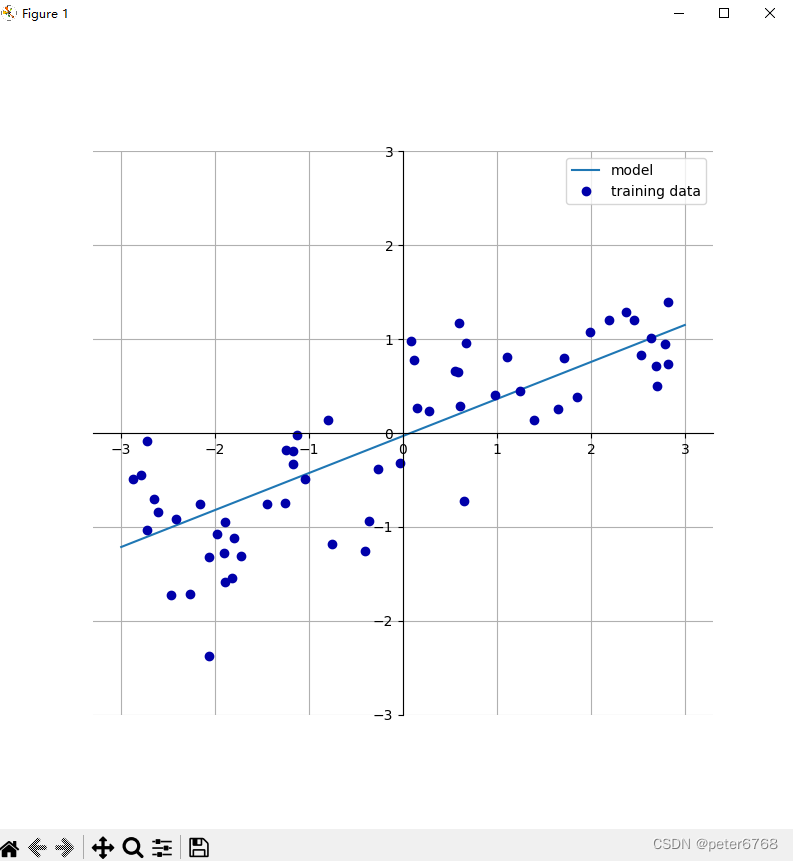
4.2 最小二乘法

也是线性拟合，不同之处是使所有样本点方差之和最小，在此条件下的拟合是最小二乘法

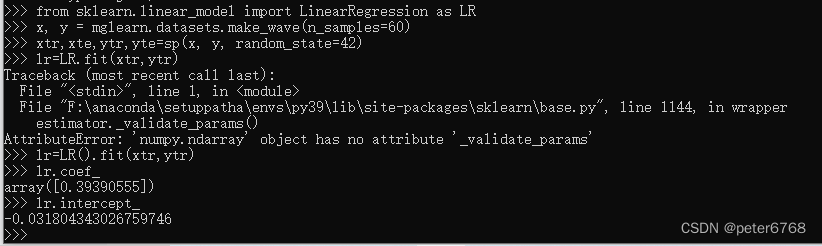
 lr对象就是拟合的结果，即一个直线方程，斜率是lr.coef_, 截距是lr.intercept_

lr.coef_是个数组，因为支持多个特征值拟合，n个特征值，coef_长度就为n

4.2.1 拟合性能

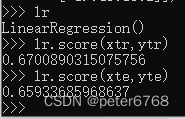
发现训练集和测试集R平方为0.67 ，0.65，可能是欠拟合而不是过拟合

4.2.2 波士顿房价拟合

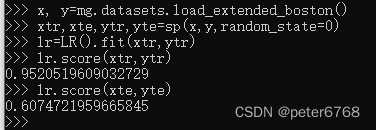
发现训练集很准 ，测试集不太准。训练集和测试集存在差异时，可能是过拟合的表现，需要找一个可以控制复杂度的模型，一个替代方法是岭回归

4.2.3 优缺点

无参数，方便，但无参导致无法控制模型复杂度

4.3 岭回归

与最小二乘法区别：公式一样都是线性公式，不同是增加了正则的附加约束，即每个特征值相互影响尽可能小，这要求每个特征值的系数在准确拟合结果的情况下尽可能小（也就是趋于0）。正则可以减少过拟合，也叫L2正则化

用岭回归对波士顿房价进行拟合

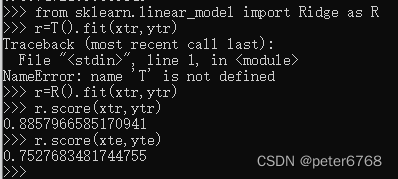
 发现训练集和测试集之间拟合度差值缩小了

LR(alpha=xx)可传入alpha值，值越小越靠过拟合，反之亦然。alpha=0表示不做正则化处理，alpha不为0表示做正则化处理

对一般线性回归，岭回归做评估准度随样本数增加的图

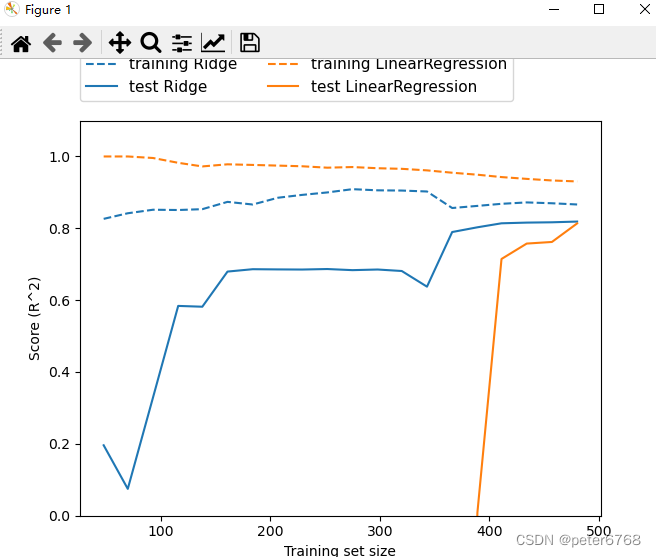
 可发现，岭回归相比于线性回归，训练集精度小，因为斜率降低导致精度下降，但测试集精度上升，是因为斜率小了，样本间y值之差也小了

4.4 lasso

在线性回归上加了L1的正则化，和L2正则化不同的是，将某些系数接近0的特征值的系数近似于0，可简化模型，使模型只受主要特征的影响，忽略影响小的特征。对波士顿数据集看下模型训练精度

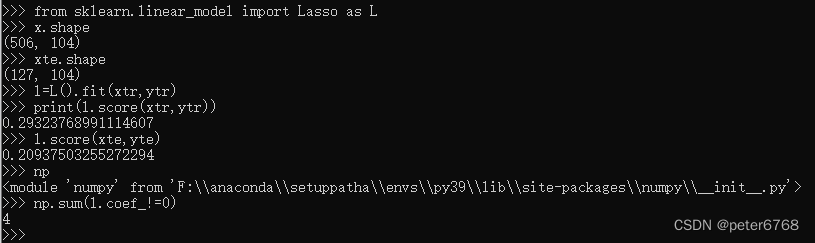
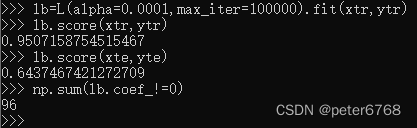
 发现训练集和测试集的精度都不高，应该存在欠拟合，看到特征值只有4个不为0

可减小alpha增大模型复杂度

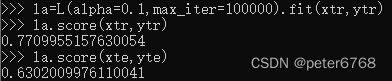
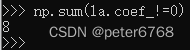
发现训练集和测试集准确性随特征值数增加提升了 

如果alpha太小会发生过拟合，训练集准确度会比测试集的高很多，结果会趋近于LineRegression

看下不同alpha的lasso和ridge特征值

 

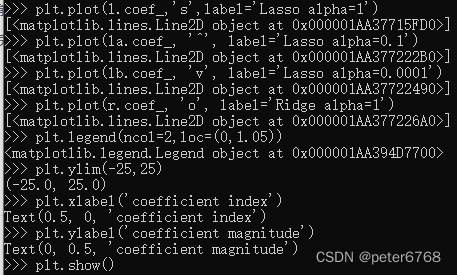
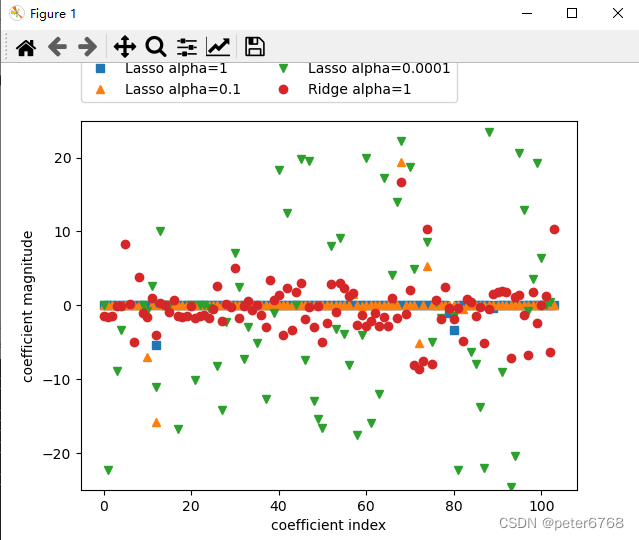
 4.5 小结

在岭回归和lasso中一般选岭回归，如果是需要关注某几个模型，可以使用lasso。scikit-learn还提供了个岭回归和lasso的结合体Elastic-Net，不过各自的正则参数需要自己调

4.6 分类线性模型

之前的几种模型（最小二乘法，岭回归，lasso）都是解决回归问题，现在看几个解决分类的线性模型

公式与回归类似，结果只有大于0和小于0，分别代表两种分类结果。线性模型决策边界也是线性，比如直线，平面等

区分线性模型算法也类似于回归，看斜率、截距和正则化影响

两种常见线性分类方法是logistic回归和线性支持向量机（linear support vector machine,也称线性svm,在svm.linearSVC中，support vector classifier），分别在linear_model.LogisticRegression和svm.LinearSVC中实现,两个模型都用到了L2正则化

4.6.1 SVC

可用这两种给分类数据集找决策边界

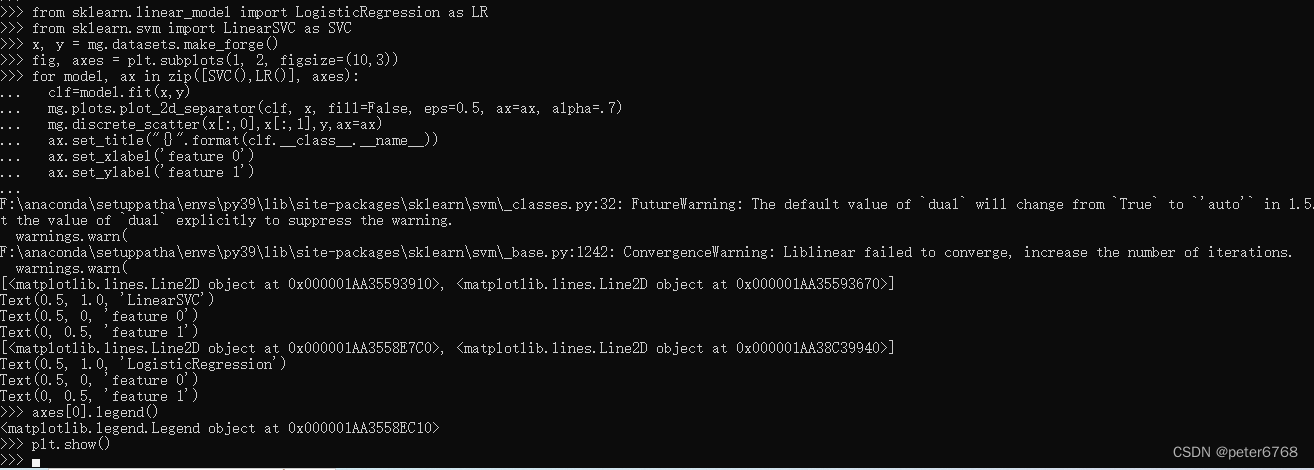
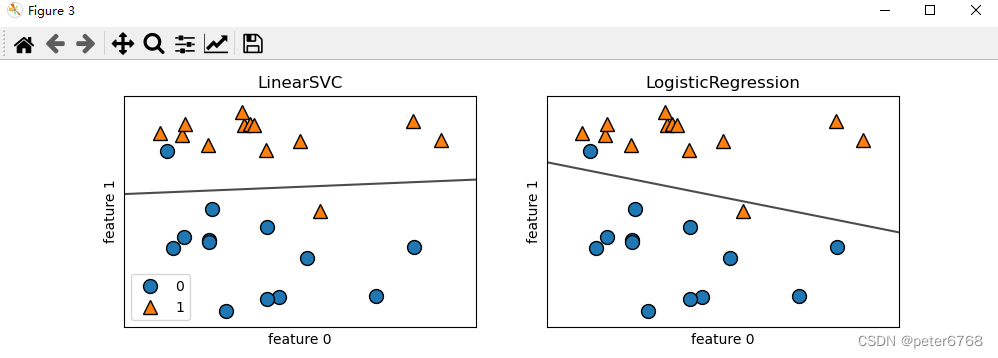
 LinearSVC和LogisticRegression的正则化强度取决于一个权衡系数C，正则化强度与C大小成反比

如果C趋于0，则正则化程度极大，意味着训练得到的特征值的特征系数趋近于0

如果C很大，则正则化程度极小，意味着完美拟合所有测试集，可能出现过拟合

看下效果

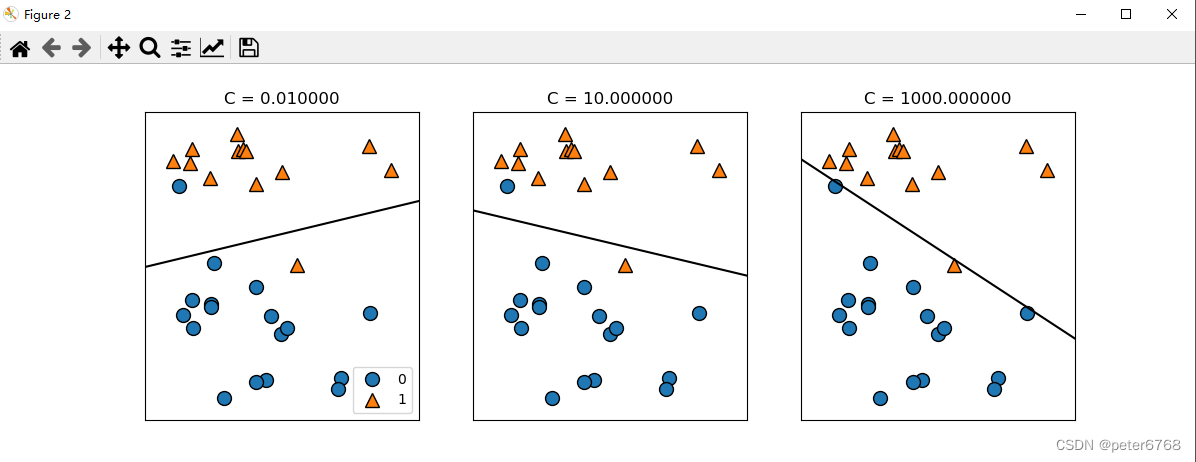
 含义同上

c小，正则化效果强，导致很多特征值趋于0（正交），简化模型，欠拟合

c大，正则化效果小，每个特征值都占影响比重，出现过拟合，训练集准度高，测试集准度低

4.6.2 logisticregression

看下泛化准确度，logisticregression的正则化系数C默认为1

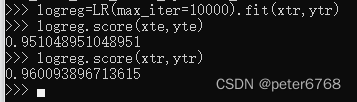
 训练集和测试集准确度接近，可能欠拟合，增大C值提高拟合度

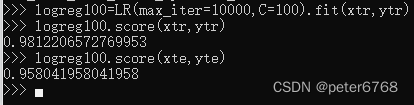
 减小C值再看下

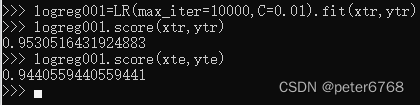
 看下LogisticRegression三个C值的特征系数

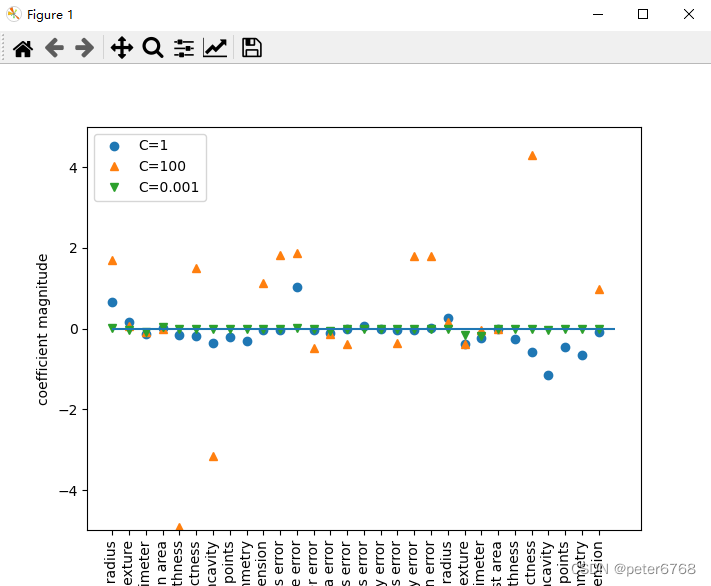
 起作用的特征值比较多，如果想专注某几个特征值，可以用L1正则化

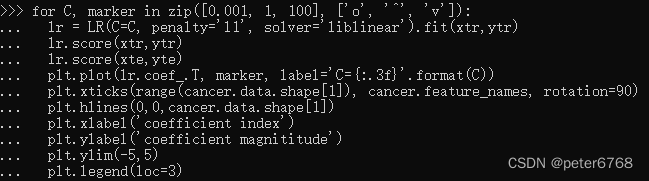
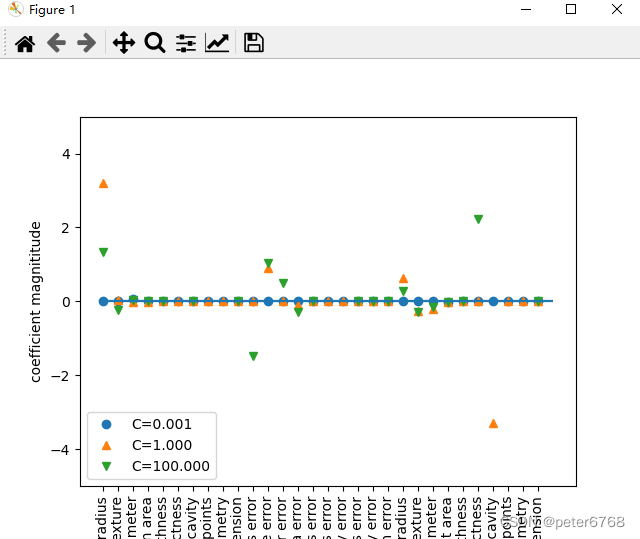
 4.7 多分类线性模型

即多分类问题，一种是多次用二分类实现多分类，logisticregression也可以适用于多分类

4.7.1 多分类数据集

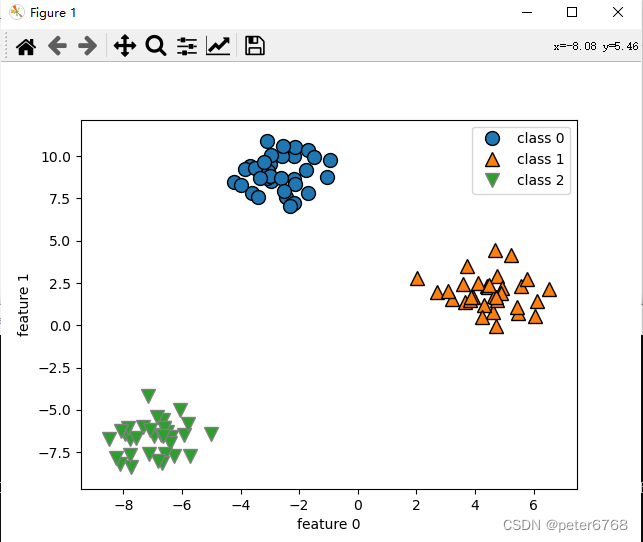
 4.7.2 用SVC多分类

训练一个分类器，查看分类器决策边界斜率和截距

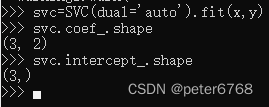
 斜率包含了两个特征值的斜率，所以是(3,2),对三个二分类器进行可视化

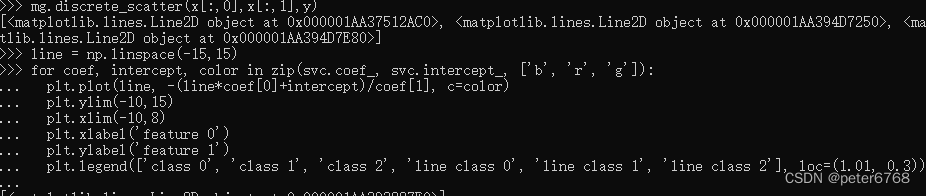
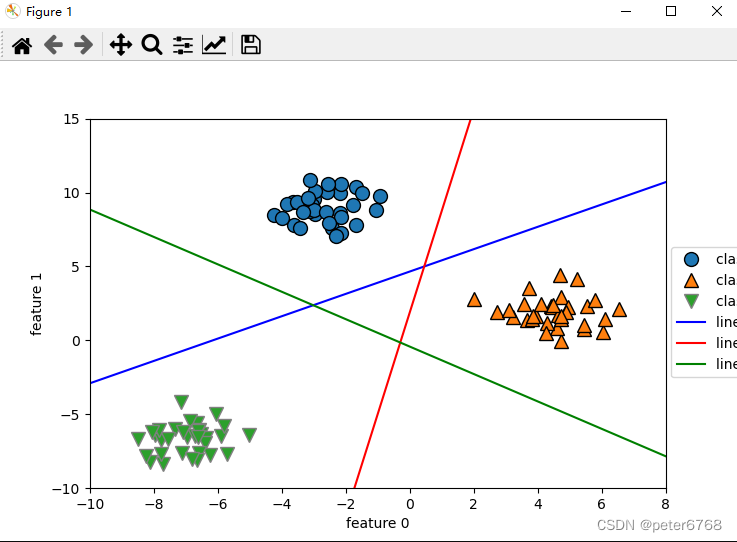
 理解下直线公式怎么来的，因为是三分类数据集，y会有三个值，训练时会两两进行二分类，会有三组coef值，决策边界可以理解为一条直线公式ax+by=0，将y用x表示的公式就是直线公式

三条直线中间围成了一小块空白，没有任何点在里面，分类器将这块趋于算为方程结果最多的哪一类

看下所有区域预测结果

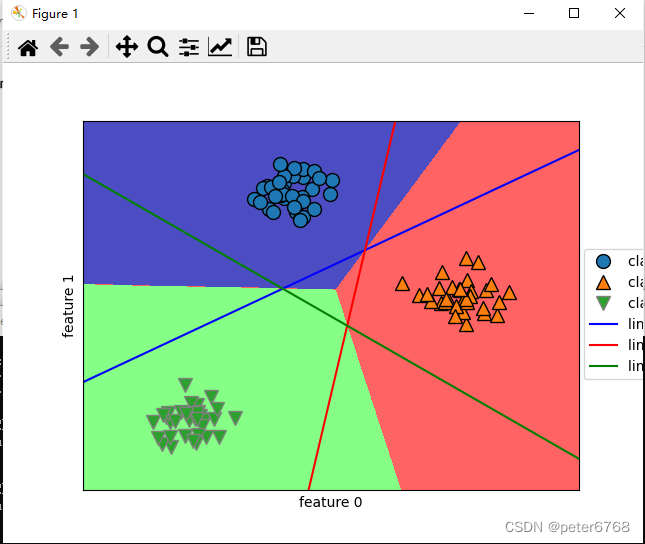
 4.8 优缺点

正则化参数在分类问题好像叫C，在回归问题叫alpha

alpha较大或C较小说明模型简单，使用正则化注意区分需要L1正则化还是L2正则化

4.8.1 优点

线性模型训练速度和预测速度都很快，对稀疏矩阵也很有效，如果处理大型数据，需要考虑参数solver='sag'选项，因为处理大型数据时，此选项会加快处理速度

4.8.2 缺点

无法对高度相关的特征进行针对性分析，无法解释为什么特征系数是这样的

4.8.3 模型适用场景

特征数量大于样本数量时 或数据量较大场景 线性模型较好 因为其他模型不太行

特征数量较少时 有其他更合适的模型

5 朴素贝叶斯分类器

性能 贝叶斯分类器和线性模型相似，但速度更快。代价是泛化能力比线性模型较差(LogisticRegression/SVC)。MultinomialNB性能要优于BernouliNB

性能高效的原因 贝叶斯分类器高效的原因是，单独查看每个特征值来学习特征参数，从每个特征收集简单类别统计数据，scikit-learn实现了三种朴素贝叶斯分类器，GaussianNB，BernouliNB，MultinomialNB。

适用场景 GaussianNB可应用于任意连续数据，主要用于高维数据，NernouliNB假定输入数据为二分类数据，MultinomialNB假定输入数据为计数数据（如一个单词在句子中出现的次数），BernouliNB和MultinomialNB主要用于文本数据分类或稀疏数据统计，

原理 BernouliNB计算每个类别中每个特征值在所有样本里的计数，MultinomialNB统计每个类别中每个特征值的平均值，GaussianNB计算每个类别中每个特征值的均值和方差

预测 三个模型做预测的话，需要将数据点和每个类别特征值统计数据做对比，将最匹配的模型作为匹配结果。MultinomialNB和BernouliNB的预测公式与线性模型预测公式相同。

朴素贝叶斯模型的coef和线性模型的coef含义不太相同

优点 MultinomialNB和BernnouliNB有个参数alpha，用于控制模型复杂度，意义是给数据中添加数量为alpha的的虚拟数据点，这些点的特征值所有数值为正值，可将数据平滑化，结果是对精度会略有提高，对稀疏数据效果很好，常用于大型数据（线性模型对大型数据可能更耗时）

6 决策树

概述 决策树广泛用于分类和回归问题，本质是从一层层if/else进行学习得出结论。

来个例子

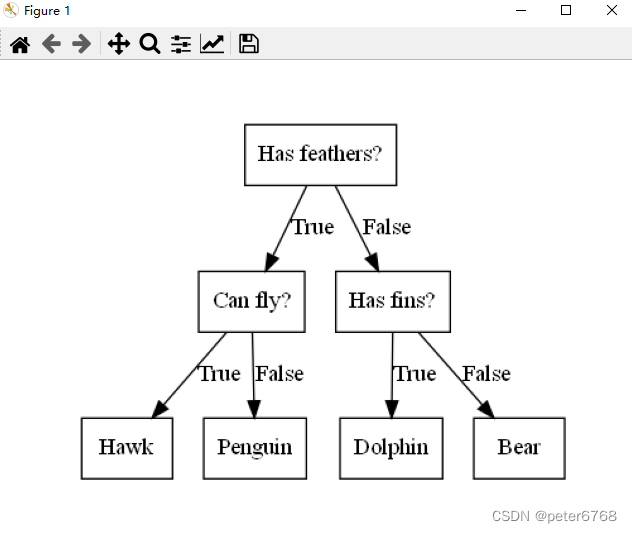
 借此例子，简单看决策树原理，即通过学习数据中特征值（是否有羽毛，是否能飞，是否有鳍）来构造模型

一般决策树问题的数据样本，不像例子一样是二分类问题，而是连续的数据，这样的话，没有现成的特征值，需要自己构造特征值，比如特征x的值是否大于xx？

Z 总结

z.1 模型汇总

k临近线性 sklearn.neighbors.KNeighborsClassifier

k临近回归 sklearn.neighbors.KNeighborsRegressor

最小二乘法 sklearn.Linear_model.LinearRegression

岭回归模型 sklearn.Linear_model.Ridge