rnn和lstm

rnn

torch.nn.RNN

看下文档

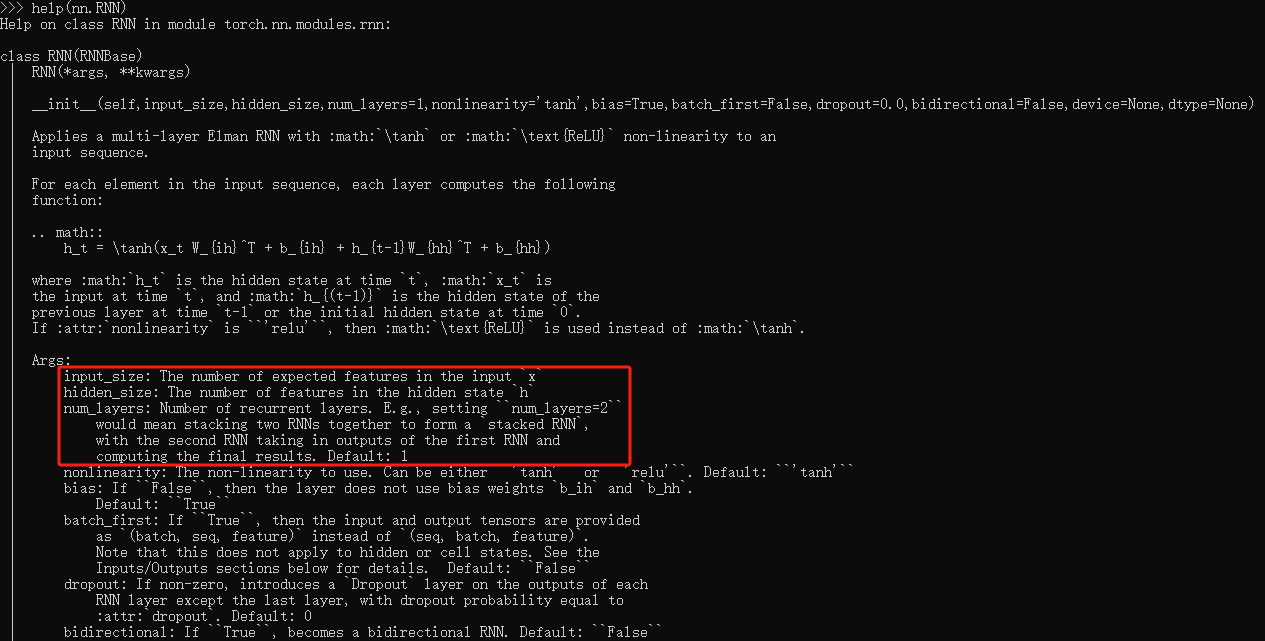
RNN(input_size, hidden_size, layers) 这行代码里，input_size是单个输入向量的长度，hidden_size是一个rnn的长度，layers是几个大小为hidden_size的rnn叠加，所以nn.RNN的每层rnn神经元数量是一样的

out, h = rnn(x, h)，其中，x和h可以添加batch数，如果x加了batch参数，h也需要加batch参数，x和h需要同步。h是rnn用来学习上一步的隐含层

例子

# 导入程序所需要的程序包

# PyTorch用的包
import torch
import torch.nn as nn
import torch.optim

from collections import Counter # 搜集器，可以让统计词频更简单

# 绘图、计算用的程序包
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import rc
import numpy as np

# 实现一个简单的RNN模型
class SimpleRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, num_layers = 1):
        # 定义
        super(SimpleRNN, self).__init__()

        self.hidden_size = hidden_size
        self.num_layers = num_layers
        # 一个embedding层
        # self.embedding = nn.Embedding(output_size, hidden_size)
        self.embedding = nn.Embedding(10, hidden_size)
        # PyTorch的RNN层，batch_first标识可以让输入的张量的第一个维度表示batch指标
        self.rnn = nn.RNN(hidden_size, hidden_size, num_layers, batch_first = True)
        # 输出的全连接层
        self.fc = nn.Linear(hidden_size, output_size)
        # 最后的LogSoftmax层
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input, hidden):
        # 运算过程
        # 先进行embedding层的计算
        # 它可以把一个数值先转化为one-hot向量，再把这个向量转化为一个hidden_size维的向量
        # input的尺寸为：batch_size, num_step, data_dim
        x = self.embedding(input)
        # 从输入层到隐含层的计算
        # x的尺寸为：batch_size, num_step, hidden_size
        output, hidden = self.rnn(x, hidden)
        # 从输出output中取出最后一个时间步的数值，注意output包含了所有时间步的结果
        # output尺寸为：batch_size, num_step, hidden_size
        output = output[:,-1,:]
        # output尺寸为：batch_size, hidden_size
        # 把前面的结果输入给最后一层全连接网络
        output = self.fc(output)
        # output尺寸为：batch_size, output_size
        # softmax函数
        output = self.softmax(output)
        return output, hidden

    def initHidden(self):
        # 对隐含单元的初始化
        # 注意尺寸是layer_size, batch_size, hidden_size
        return torch.zeros(self.num_layers, 1, self.hidden_size)

train_set = []
valid_set = []

# 生成的样本数量
samples = 2000

# 训练样本中n的最大值
sz = 10
# 定义不同n的权重，我们按照10:6:4:3:1:1...来配置字符串生成中的n=1,2,3,4,5,...
probability = 1.0 * np.array([10, 6, 4, 3, 1, 1, 1, 1, 1, 1])
# 保证n的最大值为sz
probability = probability[ : sz]
# 归一化，将权重变成概率
probability = probability / sum(probability)

print(1)
# 开始生成samples个样本
for m in range(samples):
    # 对于每一个生成的字符串，随机选择一个n，n被选择的权重被记录在probability中
    n = np.random.choice(range(1, sz + 1), p = probability)
    # 生成这个字符串，用list的形式完成记录
    inputs = [0] * n + [1] * n
    # 在最前面插入3表示起始字符，2插入尾端表示终止字符
    inputs.insert(0, 3)
    inputs.append(2)
    train_set.append(inputs) # 将生成的字符串加入训练集train_set中

# 再生成samples/10的校验样本
for m in range(samples // 10):
    n = np.random.choice(range(1, sz + 1), p = probability)
    inputs = [0] * n + [1] * n
    inputs.insert(0, 3)
    inputs.append(2)
    valid_set.append(inputs)

# 再生成若干n超大的校验样本
for m in range(2):
    n = sz + m
    inputs = [0] * n + [1] * n
    inputs.insert(0, 3)
    inputs.append(2)
    valid_set.append(inputs)
np.random.shuffle(valid_set)

rnn = SimpleRNN(input_size = 4, hidden_size = 2, output_size = 3)
criterion = torch.nn.NLLLoss()
optimizer = torch.optim.Adam(rnn.parameters(), lr = 0.001)

num_epoch = 50
results = []
for epoch in range(num_epoch):
    train_loss = 0
    # 随机打乱train_set中的数据，以保证每个epoch的训练顺序都不一样
    np.random.shuffle(train_set)
    # 对train_set中的数据进行循环
    for i, seq in enumerate(train_set):
        loss = 0
        hidden = rnn.initHidden()  # 初始化隐含神经元
        # 对每一个序列的所有字符进行循环
        for t in range(len(seq) - 1):
            # 当前字符作为输入，下一个字符作为标签
            x = torch.LongTensor([seq[t]]).unsqueeze(0)
            # x尺寸：batch_size = 1, time_steps = 1, data_dimension = 1
            y = torch.LongTensor([seq[t + 1]])
            # y尺寸：batch_size = 1, data_dimension = 1
            output, hidden = rnn(x, hidden) # RNN输出
            # output尺寸：batch_size, output_size = 3
            # hidden尺寸：layer_size =1, batch_size=1, hidden_size
            loss += criterion(output, y) # 计算损失函数
        loss = 1.0 * loss / len(seq) # 计算每个字符的损失数值
        optimizer.zero_grad() # 清空梯度
        loss.backward() # 反向传播，设置retain_variables
        optimizer.step() # 一步梯度下降
        train_loss += loss # 将字符的损失进行累加，得到损失函数值
        # 打印结果
        if i > 0 and i % 500 == 0:
            print('第{}轮，第{}个，训练Loss：{:.2f}'.format(epoch, i, train_loss.data.numpy() / i))

    # 在校验集上测试

    valid_loss = 0
    errors = 0
    show_out = ''
    for i, seq in enumerate(valid_set):
    # 对valid_set中的每一个字符串进行循环
        loss = 0
        outstring = ''
        targets = ''
        diff = 0
        hidden = rnn.initHidden() # 初始化隐含神经元
        for t in range(len(seq) - 1):
            # 对每一个字符进行循环
            x = torch.LongTensor([seq[t]]).unsqueeze(0)
            # x尺寸：batch_size = 1, time_steps = 1, data_dimension = 1
            y = torch.LongTensor([seq[t + 1]])
            # y尺寸：batch_size = 1, data_dimension = 1
            output, hidden = rnn(x, hidden)
            # output尺寸：batch_size, output_size = 3
            # hidden尺寸：layer_size =1, batch_size=1, hidden_size
            mm = torch.max(output, 1)[1][0] # 将概率最大的元素作为输出
            outstring += str(mm.data.numpy()) # 合成预测的字符串
            targets += str(y.data.numpy()[0]) # 合成目标字符串
            loss += criterion(output, y) # 计算损失函数
            diff += 1 - mm.eq(y).data.numpy()[0] # 计算模型输出字符串与目标字符串之间存在差异的字符数量
        loss = 1.0 * loss / len(seq)
        valid_loss += loss # 累积损失函数值
        errors += diff # 计算累积错误数
        if np.random.rand() < 0.1:
            # 以0.1概率记录一个输出字符串
            show_out = outstring + '\n' + targets
    # 打印结果
    print(output[0][2].data.numpy())
    print('第{}轮，训练Loss：{:.2f}，校验Loss：{:.2f}，错误率：{:.2f}'.format(epoch,
                                                       train_loss.data.numpy() / len(train_set),
                                                       valid_loss.data.numpy() / len(valid_set),
                                                       1.0 * errors / len(valid_set)
                                                       ))
    # print(show_out)
    results.append([train_loss.data.numpy() / len(train_set),
                    valid_loss.data.numpy() / len(train_set),
                    1.0 * errors / len(valid_set)
                    ])

for n in range(20):
    inputs = [0] * n + [1] * n
    inputs.insert(0, 3)
    inputs.append(2)
    outstring = ''
    targets = ''
    diff = 0
    hiddens = []
    hidden = rnn.initHidden()
    for t in range(len(inputs) - 1):
        x = Variable(torch.LongTensor([inputs[t]]).unsqueeze(0))
        # x尺寸：batch_size = 1, time_steps = 1, data_dimension = 1
        y = Variable(torch.LongTensor([inputs[t + 1]]))
        # y尺寸：batch_size = 1, data_dimension = 1
        output, hidden = rnn(x, hidden)
        # output尺寸：batch_size, output_size = 3
        # hidden尺寸：layer_size =1, batch_size=1, hidden_size
        hiddens.append(hidden.data.numpy()[0][0])
        # mm = torch.multinomial(output.view(-1).exp())
        mm = torch.max(output, 1)[1][0]
        outstring += str(mm.data.numpy())
        targets += str(y.data.numpy()[0])

        diff += 1 - mm.eq(y).data.numpy()[0]
    # 打印每一个生成的字符串和目标字符串
    print(outstring)
    print(targets)
    print('Diff:{}'.format(diff))

lstm