leetcode1143. 最长公共子序列

最新推荐文章于 2025-10-06 18:00:48 发布

原创最新推荐文章于 2025-10-06 18:00:48 发布 · 220 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #leetcode #算法

刷题专栏收录该内容

28 篇文章

订阅专栏

本文解析了LeetCode问题#1178 - 最长公共子序列，介绍了如何使用动态规划求解两个字符串的最长公共子序列长度。通过实例演示和Java代码实现，帮助读者理解算法原理并提升编程技能。

地址：https://leetcode-cn.com/problems/longest-common-subsequence/
描述：
给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列 ，返回 0 。
一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

两个字符串的公共子序列是这两个字符串所共同拥有的子序列。

实例1：

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3 。

实例2：

输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc” ，它的长度为 3 。

实例3：

输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0 。

思路：

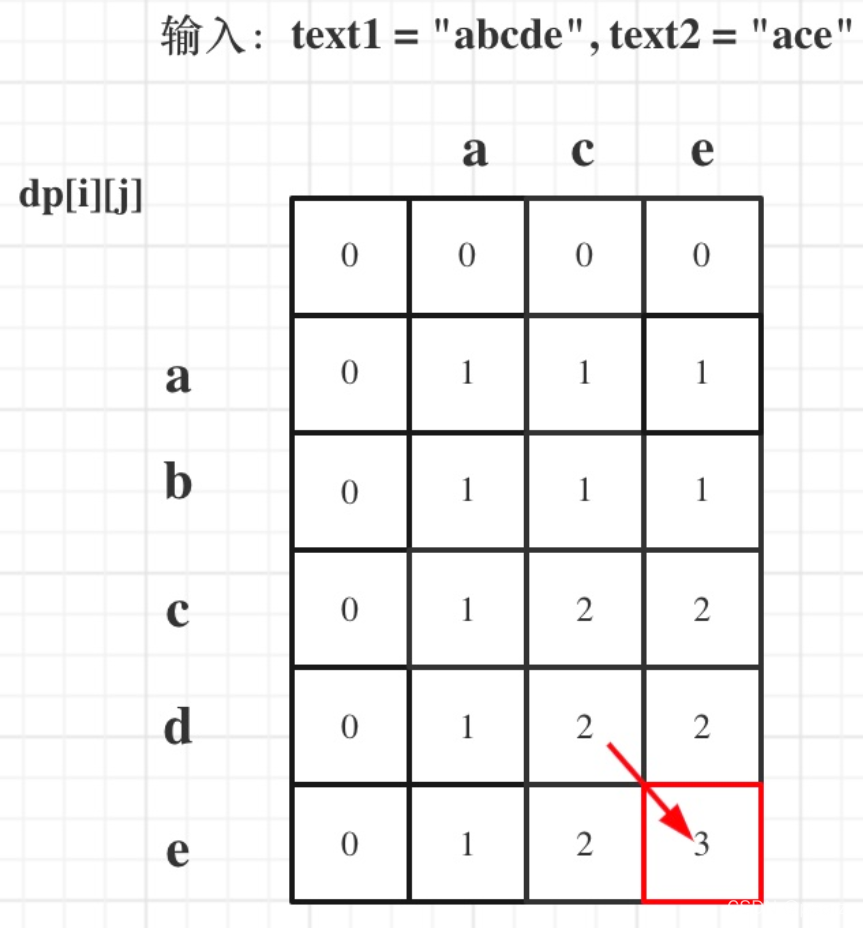
答案：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int length1 = text1.length();
        int length2 = text2.length();

        int[][] dp = new int[length1 + 1][length2 + 1];

        for (int i = 1; i <= length1; i++) {
            for (int j = 1; j <= length2; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[length1][length2];
    }
}