目录
1.1 StandardScaler(Z-score 标准化)
2. 分类报告函数:classification_report
2. TF-IDF(Term Frequency-Inverse Document Frequency)
一、Scikit-learn入门掌握
1. Python(提前掌握)
-
Python 基础语法复习
Python 基础语法包括变量、数据类型、条件语句、循环、函数、模块和面向对象编程等核心概念。掌握这些基础内容是进一步学习数据分析和科学计算的基础。
-
NumPy 数组操作
NumPy 是 Python 科学计算的核心库,提供了高性能的多维数组对象和工具。NumPy 数组操作包括数组创建、索引、切片、数学运算、广播和向量化操作等,适用于数值计算和大规模数据处理。
-
Pandas
Pandas 是一个强大的数据分析库,提供了 DataFrame 和 Series 数据结构,支持数据清洗、转换、聚合和可视化。Pandas 特别适合处理结构化数据,如 CSV、Excel 和数据库中的数据。
-
Matplotlib
Matplotlib 是 Python 中最常用的绘图库,支持生成各种静态、动态和交互式图表。它可以创建折线图、散点图、柱状图、直方图等,适用于数据可视化和探索性分析。
-
Scipy(额外)
Scipy 是一个基于 NumPy 的科学计算库,提供了许多高级数学函数和算法,包括优化、线性代数、积分、插值和统计等。Scipy 通常用于解决工程和科学领域的复杂计算问题。
2. Scikit-learn 入门
安装与配置 scikit-learn
通过 Python 包管理工具(如 pip 或 conda)安装 scikit-learn:
pip install scikit-learn
# 或 conda 用户
conda install scikit-learn
验证安装是否成功:
import sklearn
print(sklearn.__version__) # 应输出版本号(如 1.3.0)
依赖项:需提前安装 NumPy 和 SciPy。
scikit-learn 的 API 设计原则
- 一致性:所有模型的接口遵循统一规范(如
fit()、predict()、transform())。 - 可组合性:支持流水线(
Pipeline)将多个步骤串联(如标准化+分类)。 - 默认参数优化:提供合理的默认超参数,适合快速原型开发。
- 数据格式:输入数据通常为 NumPy 数组或 SciPy 稀疏矩阵。
鸢尾花分类示例
以下代码演示加载数据、训练模型和评估的完整流程:

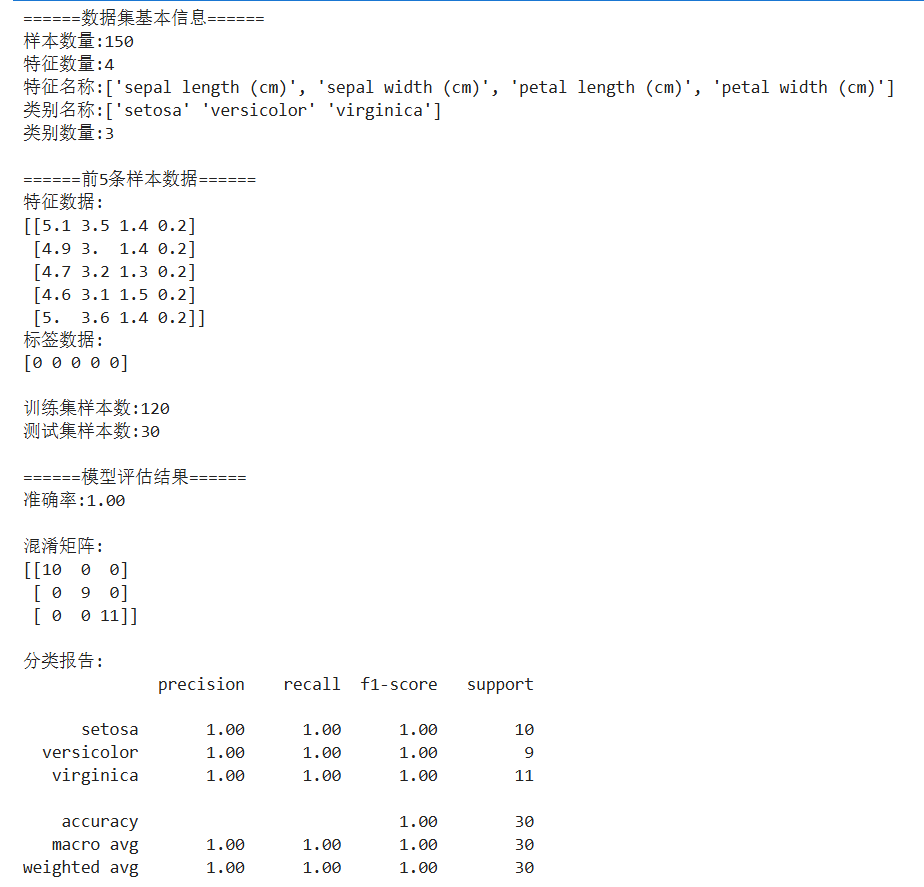
关键点说明:
load_iris()返回包含特征(data)和标签(target)的数据集。train_test_split默认划分 75% 训练集和 25% 测试集(此处调整为 80/20)。- KNN 分类器通过
n_neighbors指定近邻数,fit()方法学习数据规律。
二、数据预处理
1.数据标准化与归一化
数据标准化(Z-score标准化)将数据转换为均值为0、标准差为1的分布,适用于数据存在明显边界或需要消除量纲影响的情况。常用函数包括StandardScaler。
归一化(Min-Max标准化)将数据线性变换到固定范围(如[0,1]),适合需要统一量纲的场景,但对异常值敏感。常用函数包括MinMaxScaler。
1.1 StandardScaler(Z-score 标准化)

1.2 MinMaxScaler(区间缩放)

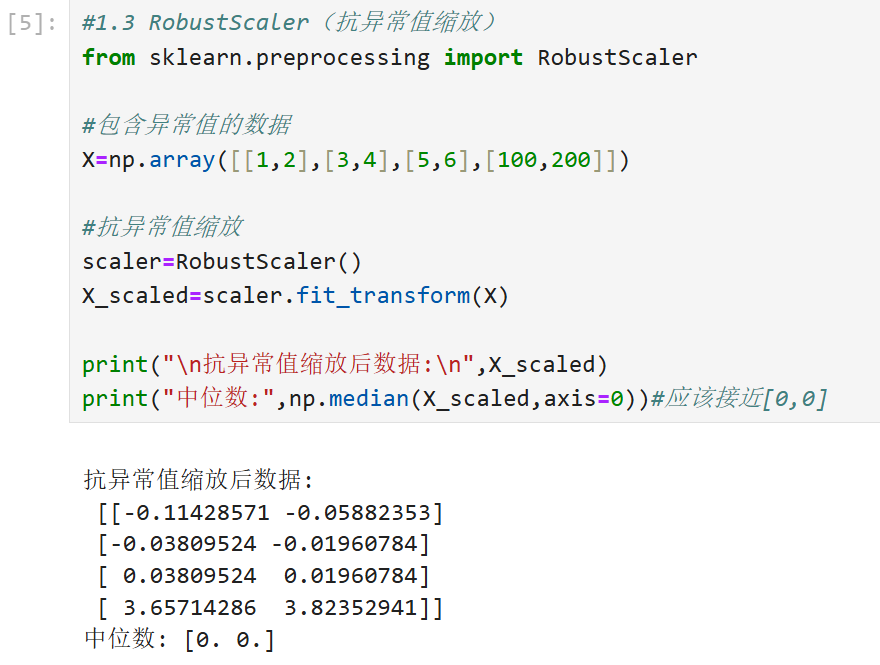
1.3RobustScaler(抗异常值缩放)
2.分类特征编码
分类变量需转换为数值形式以便模型处理。独热编码(One-Hot Encoding)为每个类别生成二进制列,适用于无序类别,函数如OneHotEncoder。
标签编码(Label Encoding)将类别映射为整数,适用于有序类别,但可能引入虚假数值关系,函数如LabelEncoder。
2.1 OrdinalEncoder(序数编码)
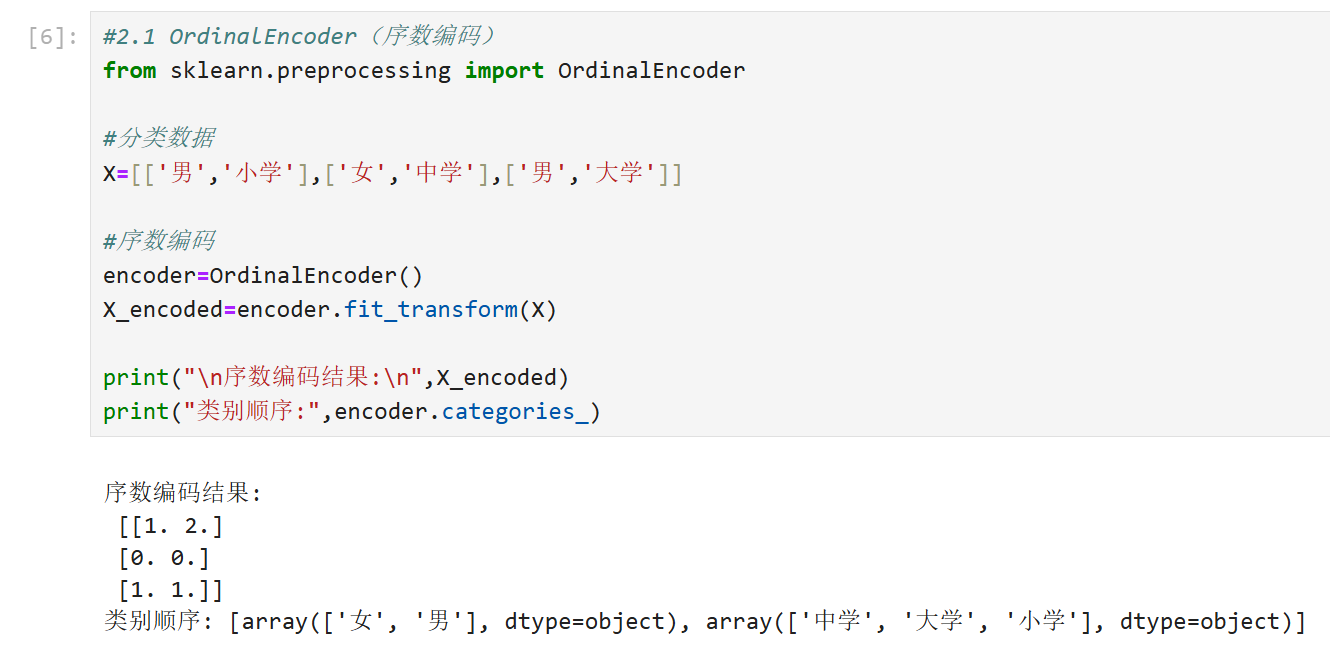
2.2 OneHotEncoder(独热编码)

3.缺失值处理
删除缺失值适用于数据量大且缺失较少的场景,函数如dropna。
填充缺失值可通过均值、中位数或众数(数值型用fillna,分类变量用SimpleImputer)。
复杂方法如模型预测(KNN、随机森林)或插值法(时间序列)需结合具体工具实现。
3.1 SimpleImputer(简单填充)
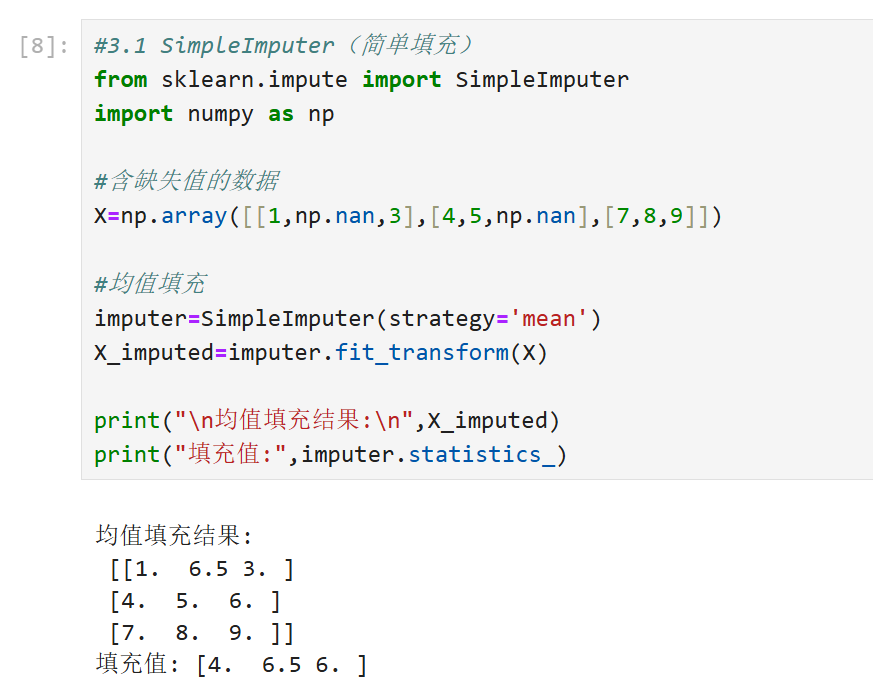
3.2 KNNImputer(K 近邻填充)

4.特征选择技术
过滤法(Filter)基于统计指标(如方差、卡方检验、互信息)筛选特征,函数如SelectKBest。
包装法(Wrapper)通过模型性能评估特征子集,如递归特征消除(RFE)。
4.1 VarianceThreshold(方差阈值)

4.2 SelectKBest(统计检验)
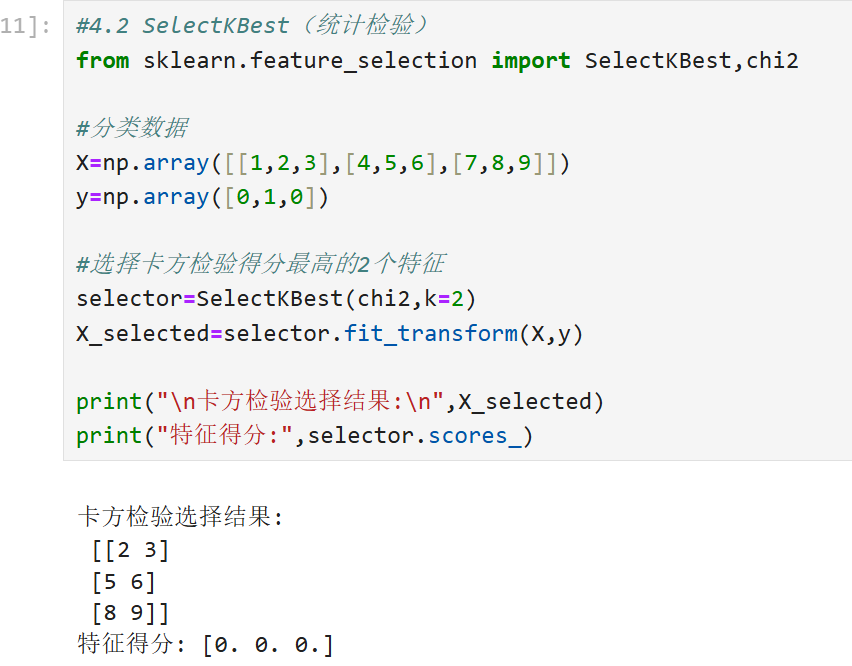
效果对比:

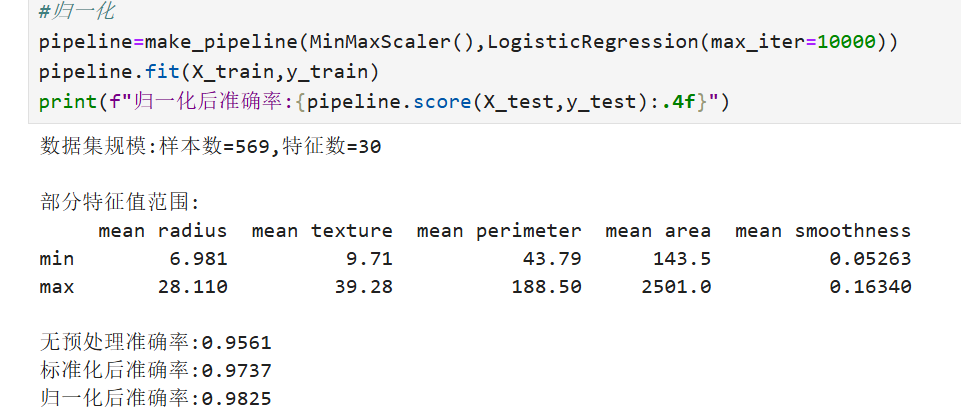
关键点总结:
1.StandardScaler适合大多数数值特征,特别是特征服从正态分布时
2.MinMaxScaler适合需要限定值范围的情况(如图像像素值)
3.OneHotEncoder会显著增加特征维度,适合类别少的特征
4.KNNImputer比简单填充更准确,但计算成本更高
5.预处理步骤应放在交叉验证的每个fold中,避免数据泄露
三、监督学习算法
1.线性回归和逻辑回归
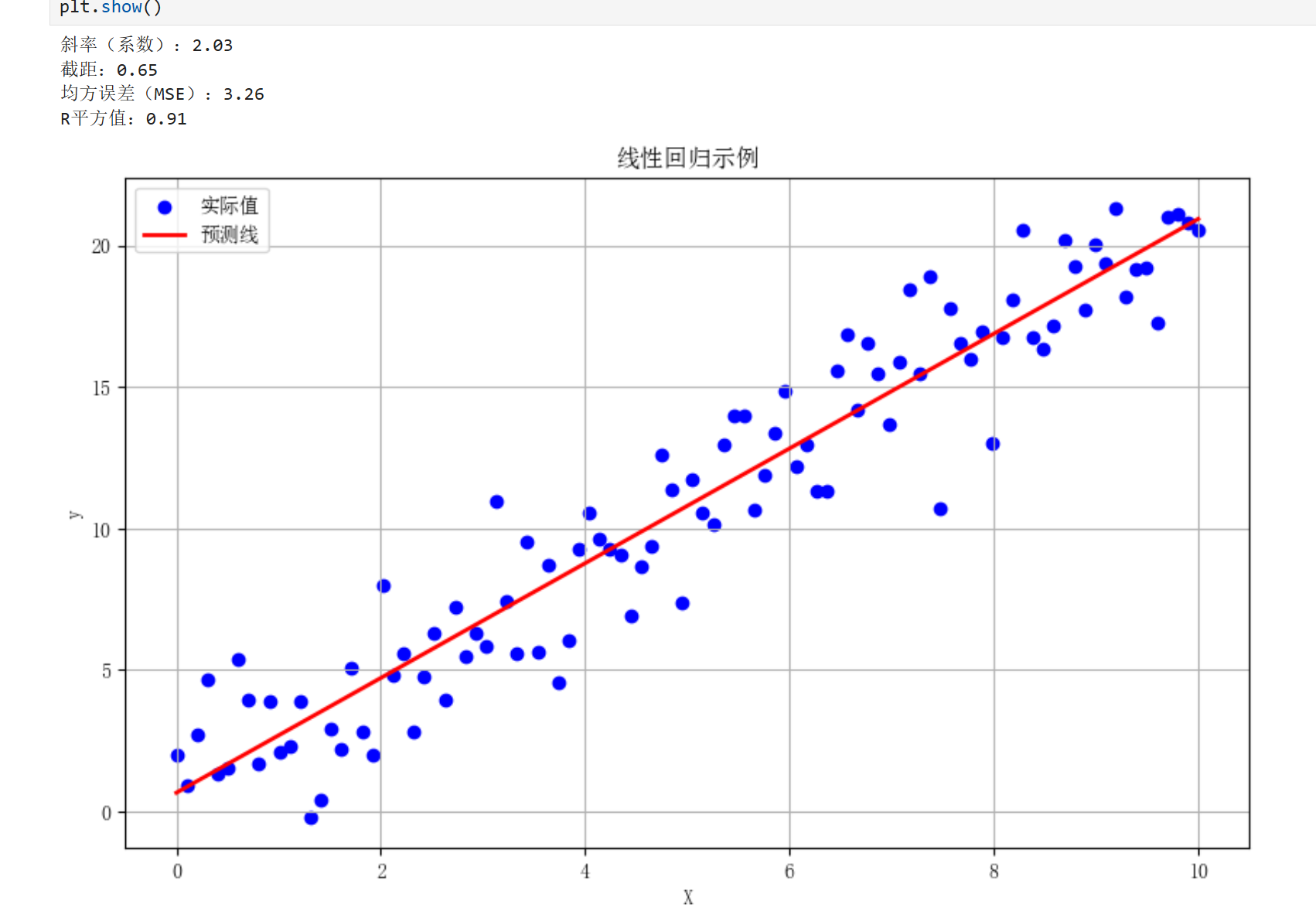
1.1线性回归
原理:通过线性方程拟合自变量(X)和连续型因变量(y)之间的关系
适用场景:
-预测连续数值结果(如房价、销售额)
-分析变量间的线性关系
-特征重要性分析
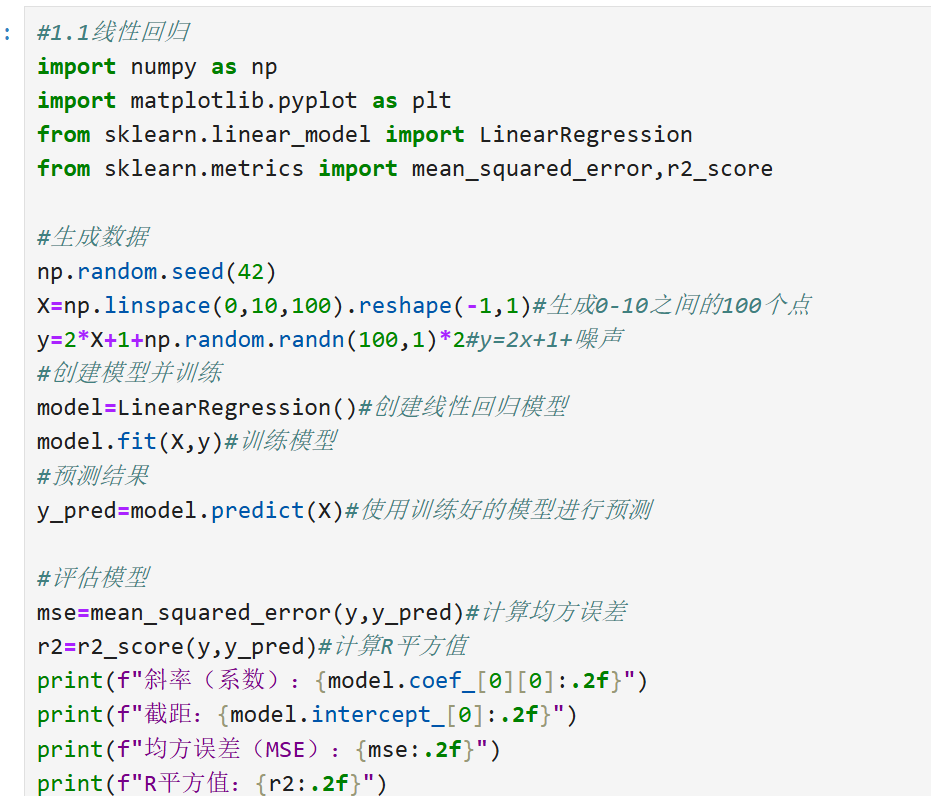
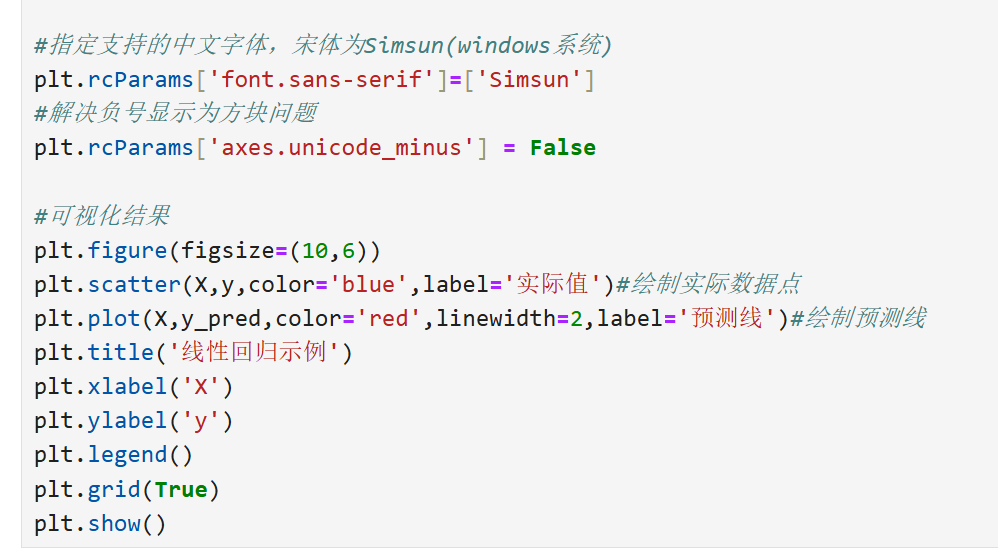
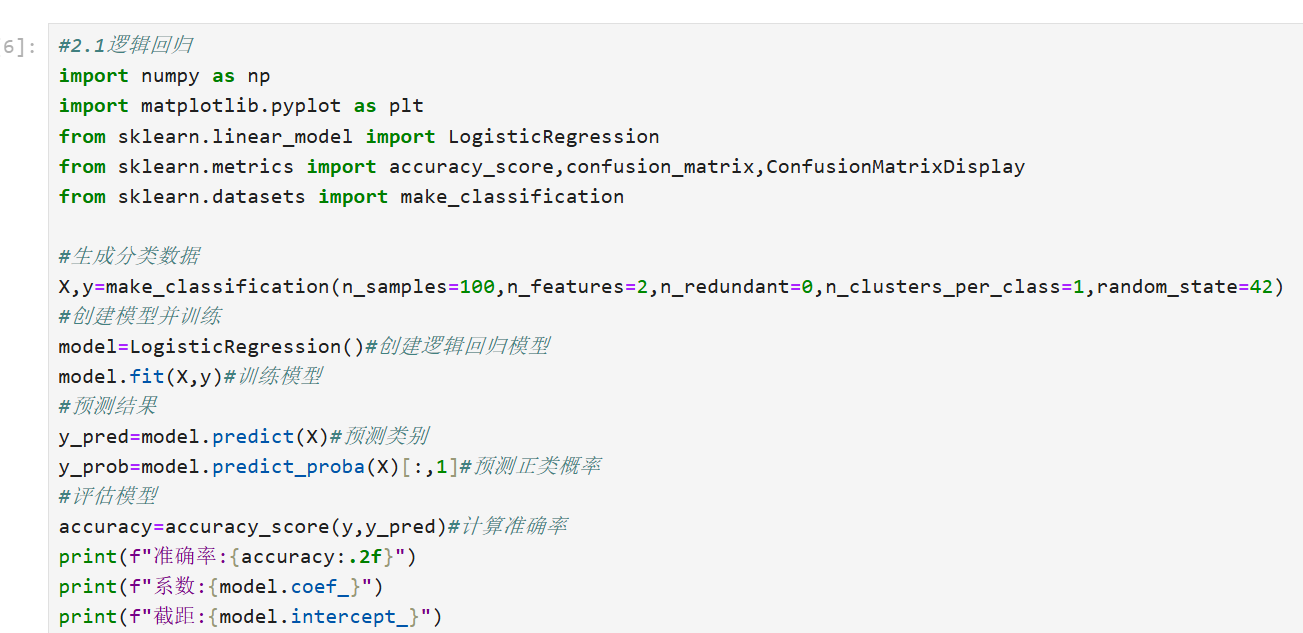
1.2逻辑回归
原理:通过sigmoid函数将线性回归结果映射到(0,1)区间,用于概率预测
适用场景:
-二分类问题(如垃圾邮件识别、疾病诊断)
-需要概率输出的分类任务
-特征重要性分析

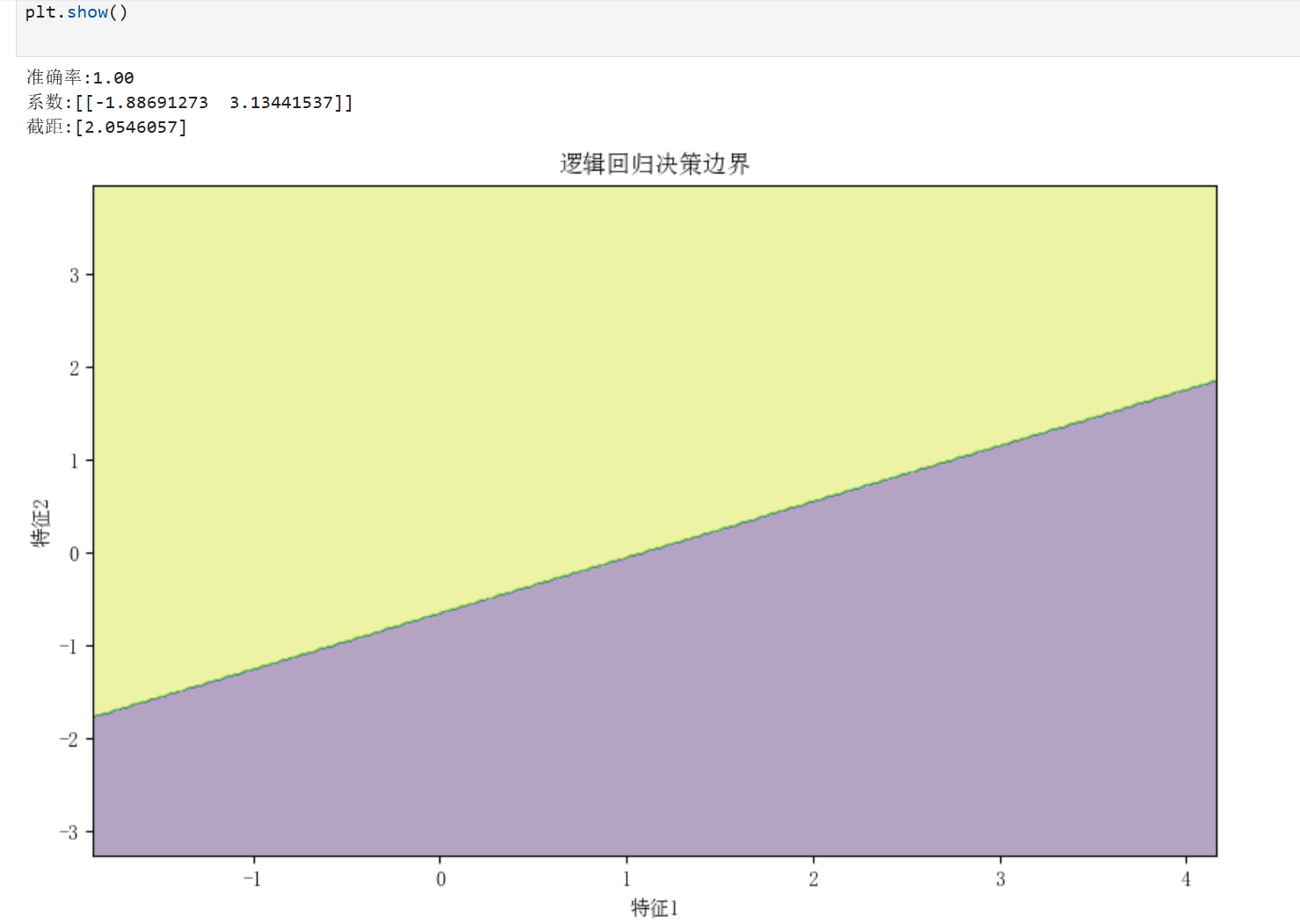
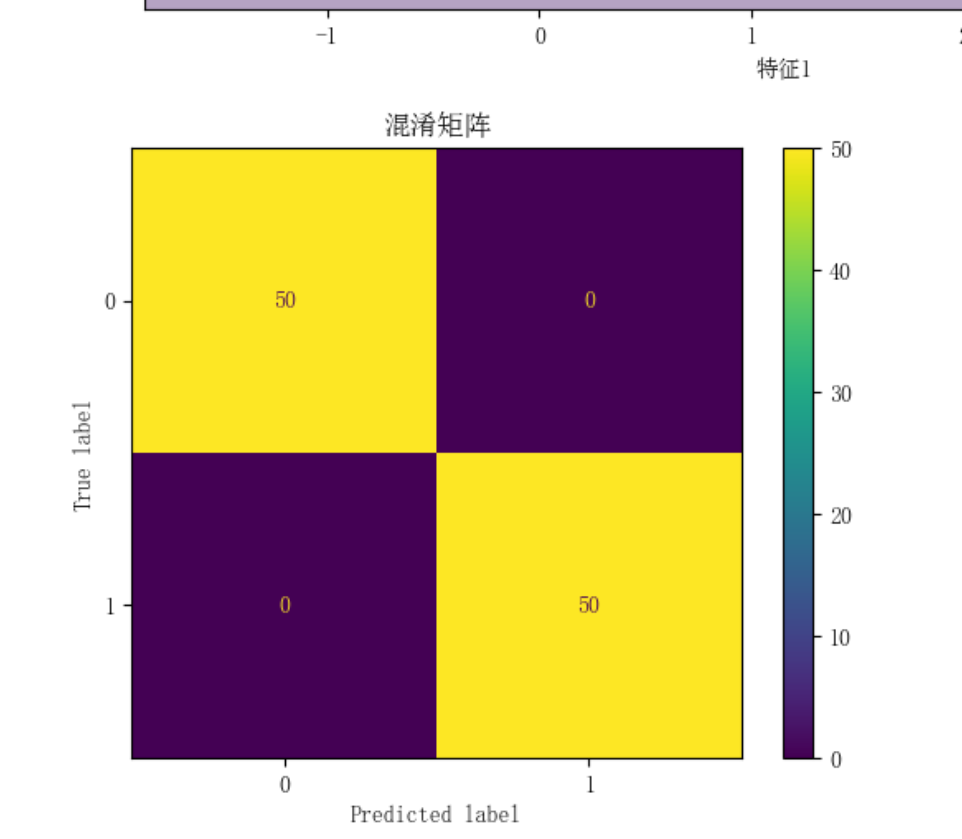
1.3两种回归对比
以下是对比线性回归和逻辑回归特性的表格:
| 特性 | 线性回归 | 逻辑回归 |
|---|---|---|
| 输出类型 | 连续值 | 概率值(0-1) |
| 目标变量 | 连续数值 | 类别标签 |
| 损失函数 | 均方误差(MSE) | 对数损失(Log Loss) |
| 应用场景 | 预测数值 | 分类问题 |
| 函数形式 | 线性 | sigmoid函数 |
1.4两种回归扩展
线性回归:

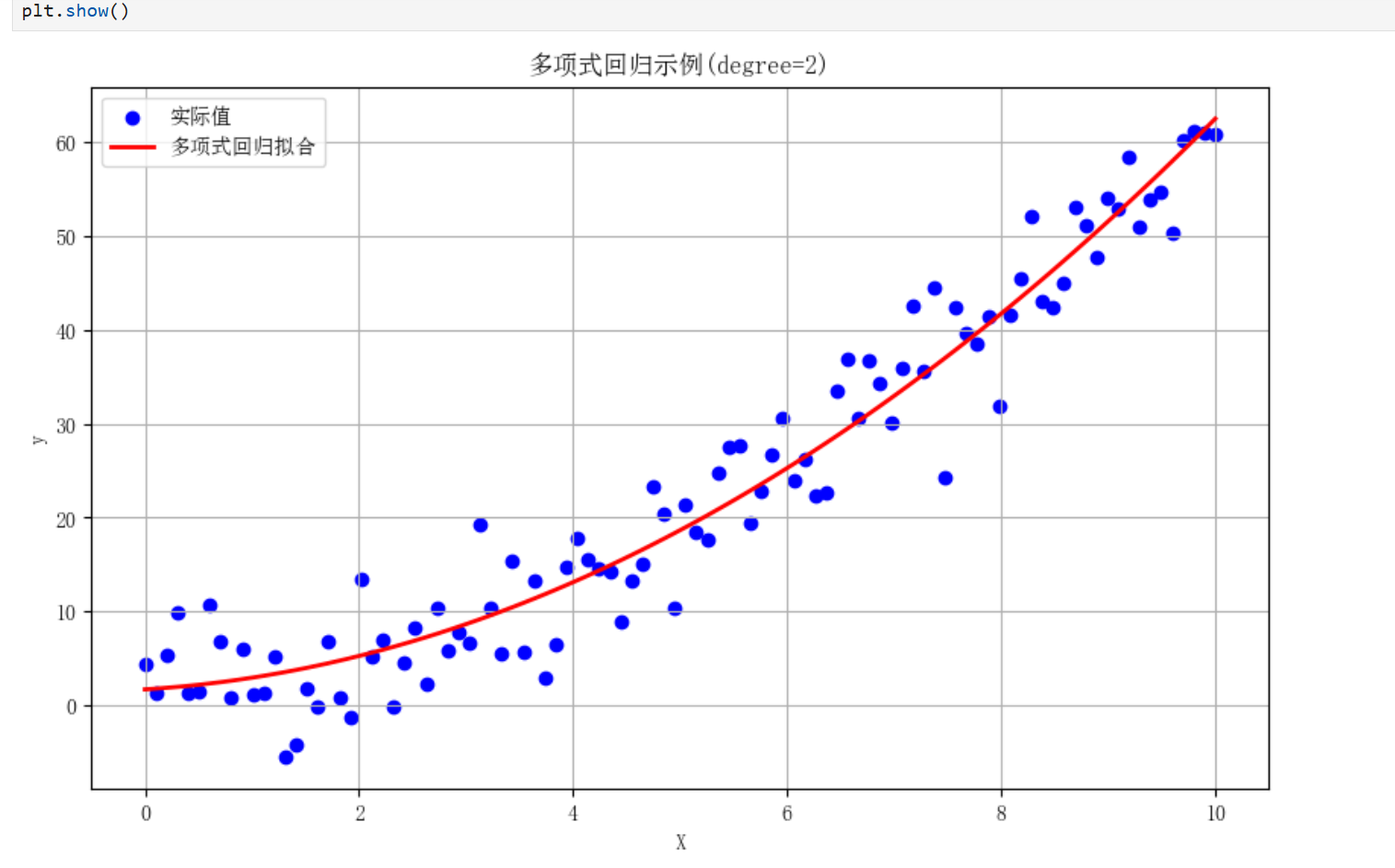
逻辑回归:
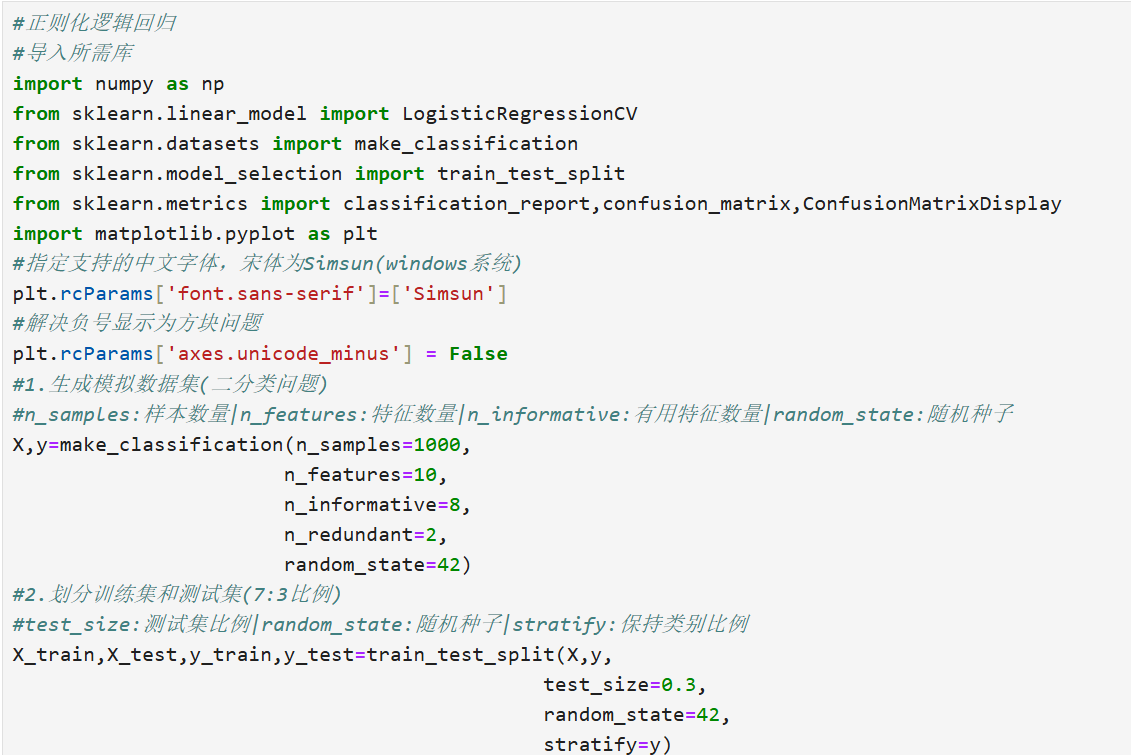

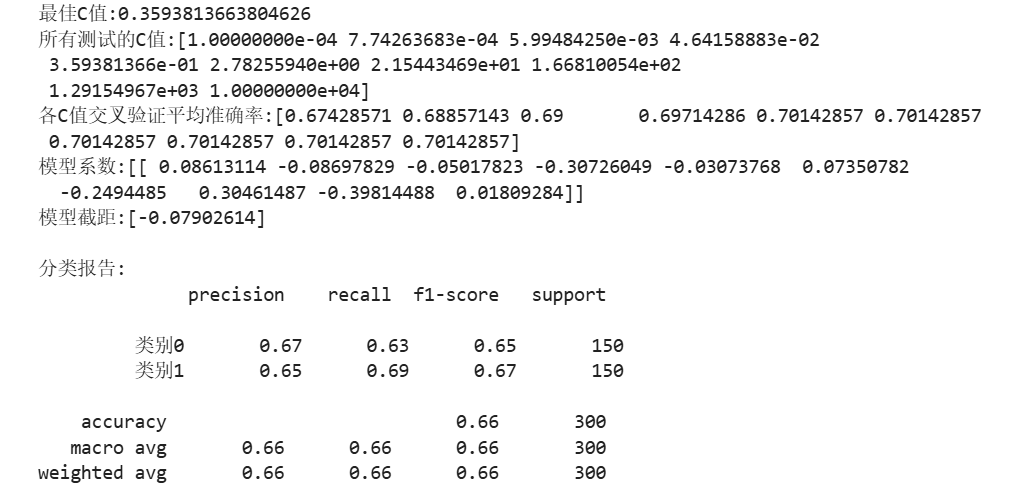

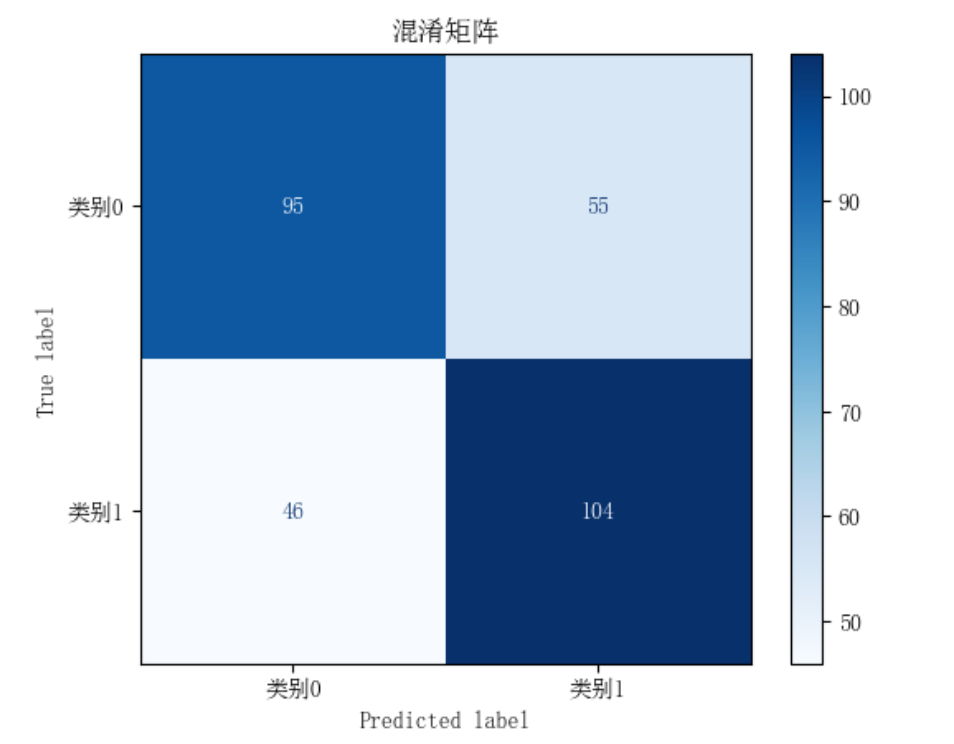
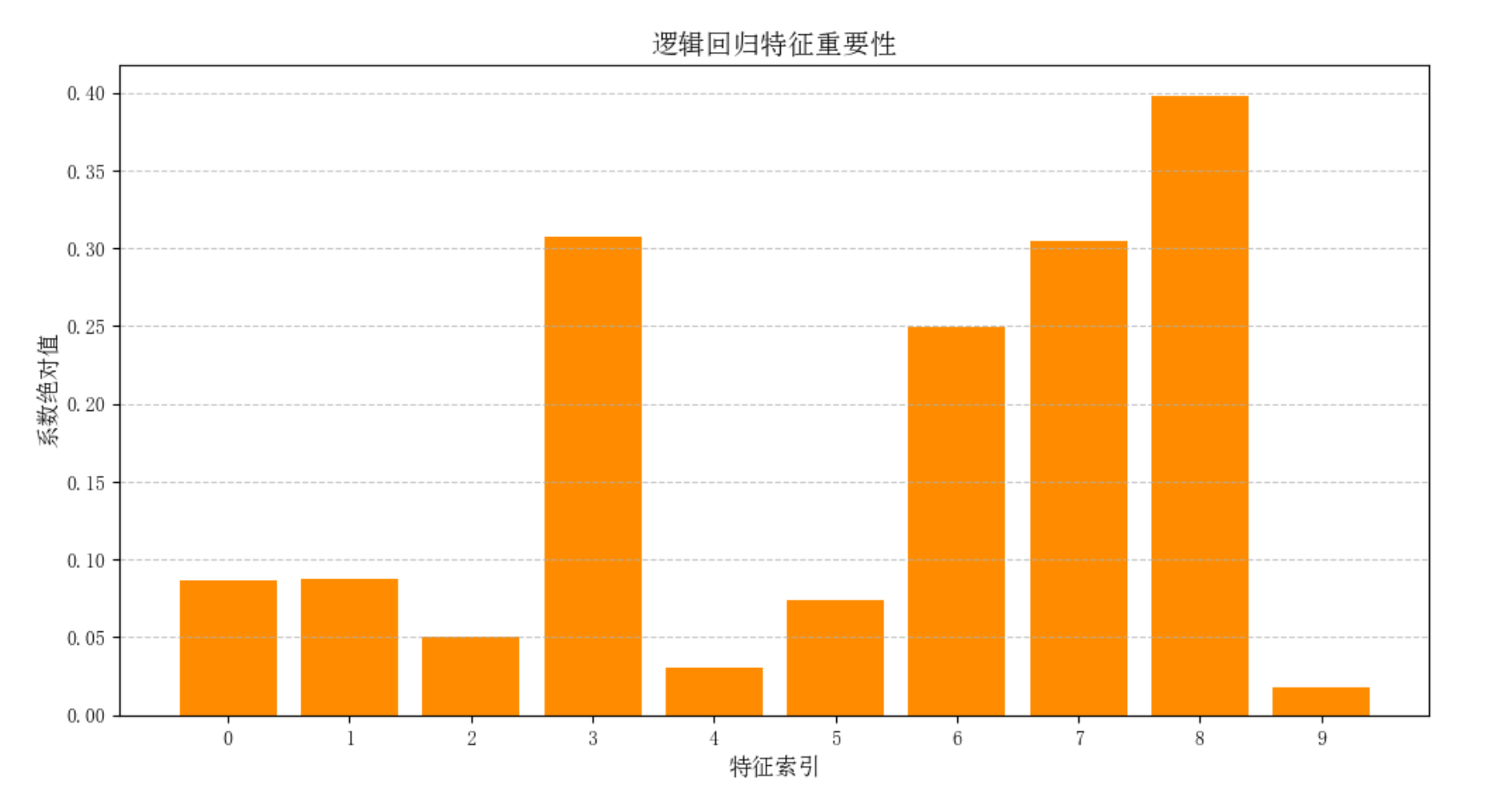
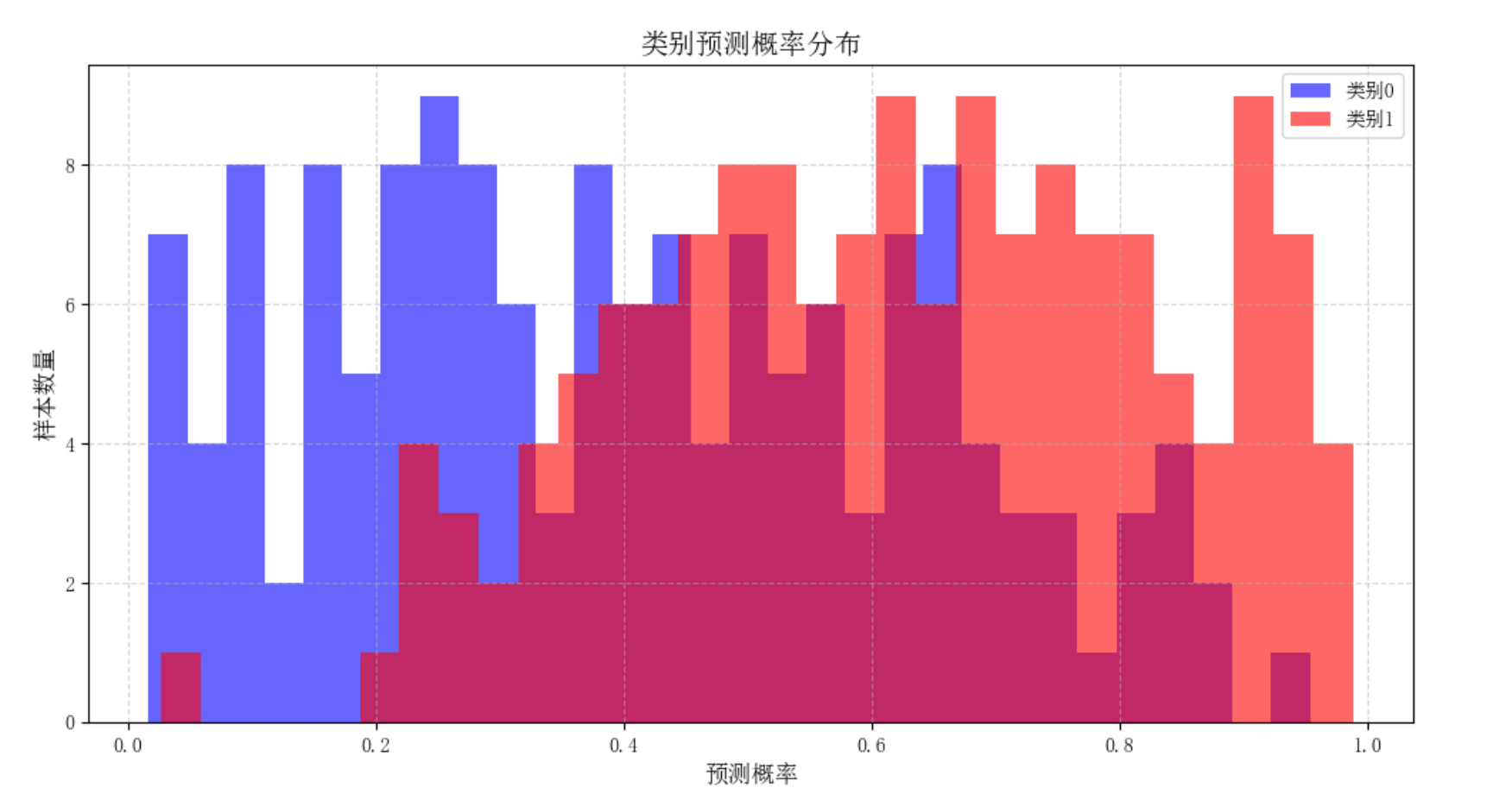
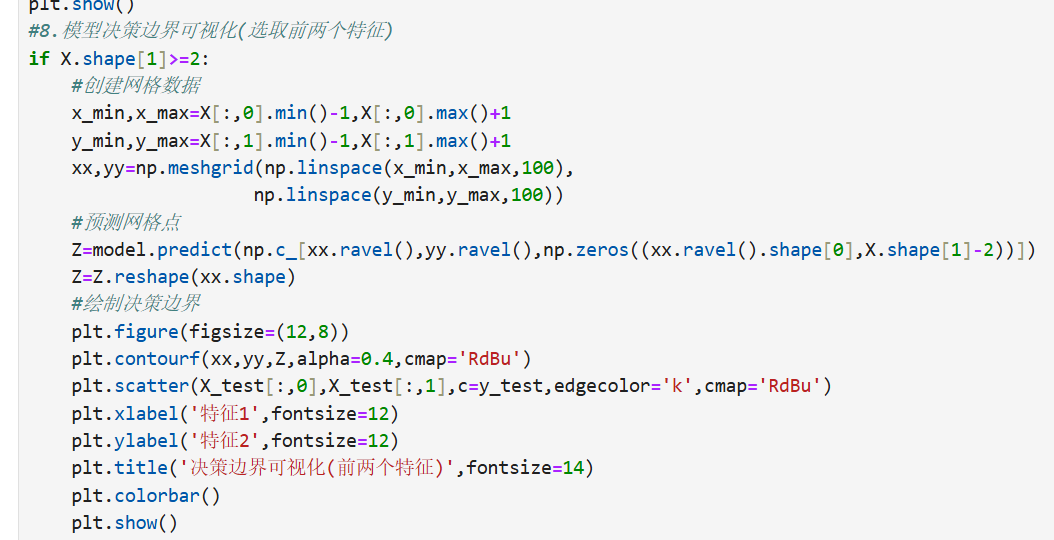
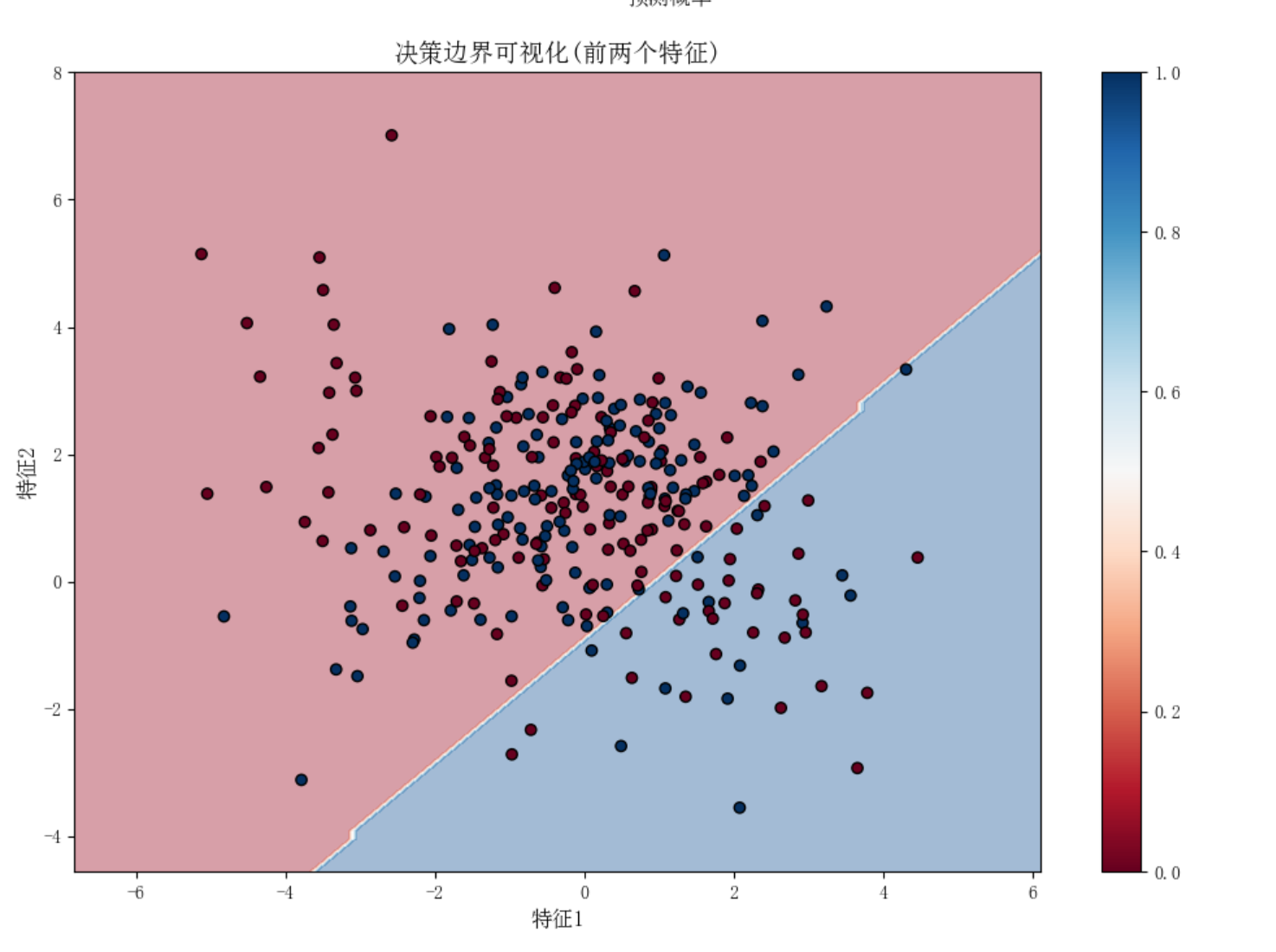
2.支持向量机(SVM)
2.1基本概念
支持向量机(SupportVectorMachine)是一种二分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器
核心思想:寻找一个最优超平面,使得两类数据点到该平面的几何间隔最大化。
-支持向量:距离超平面最近的样本点
-间隔边界:平行于超平面的两个边界平面
-核技巧:将线性不可分数据映射到高维空间实现线性可分
2.2SVM分类与回归
分类(SVC):

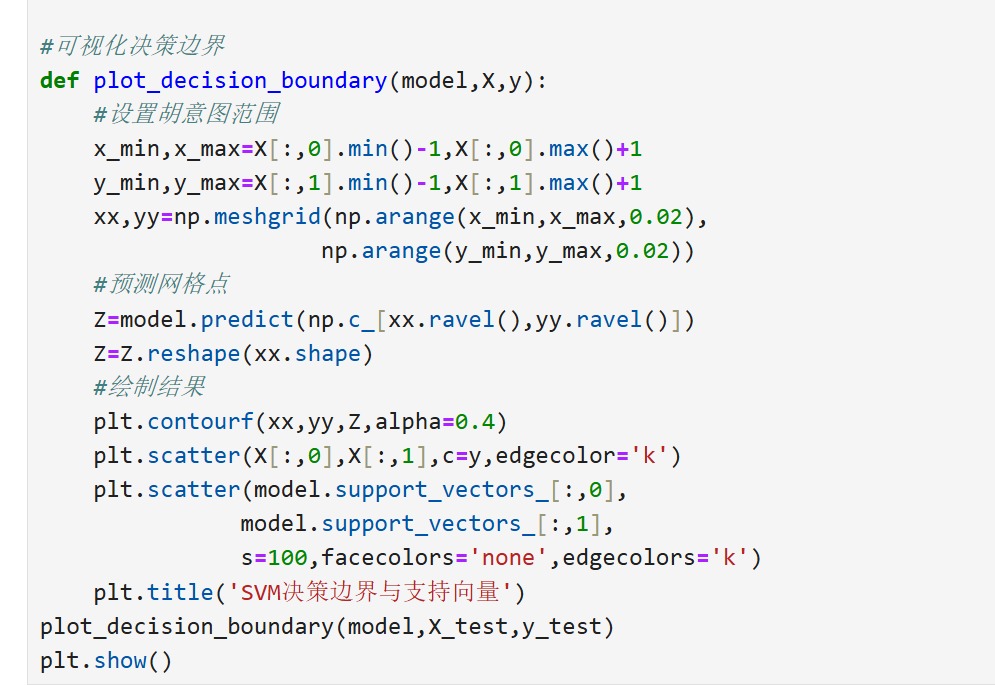
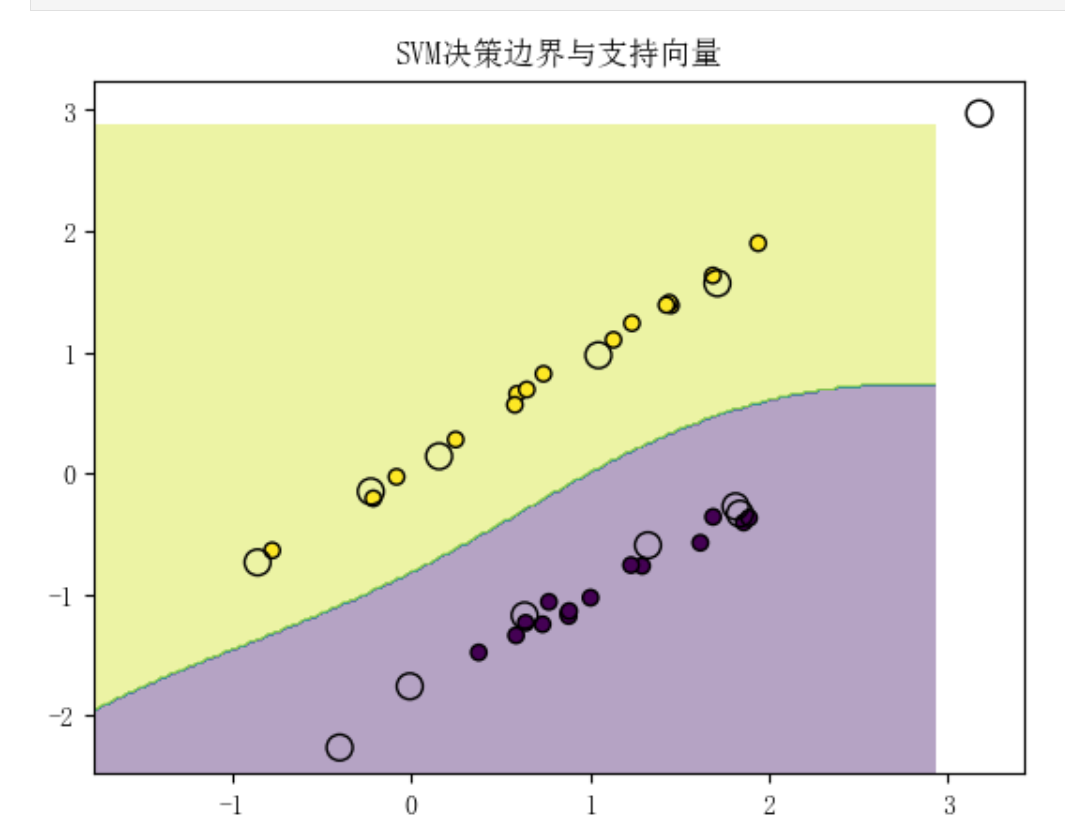
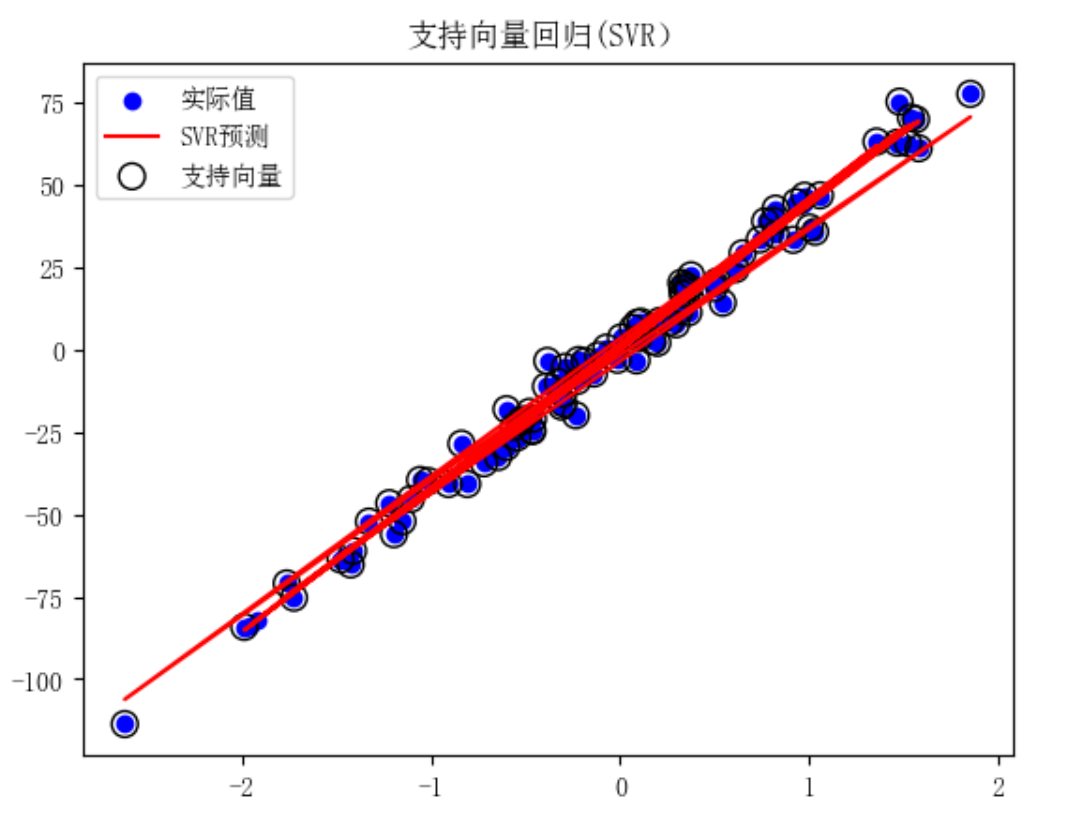
回归(SVR):

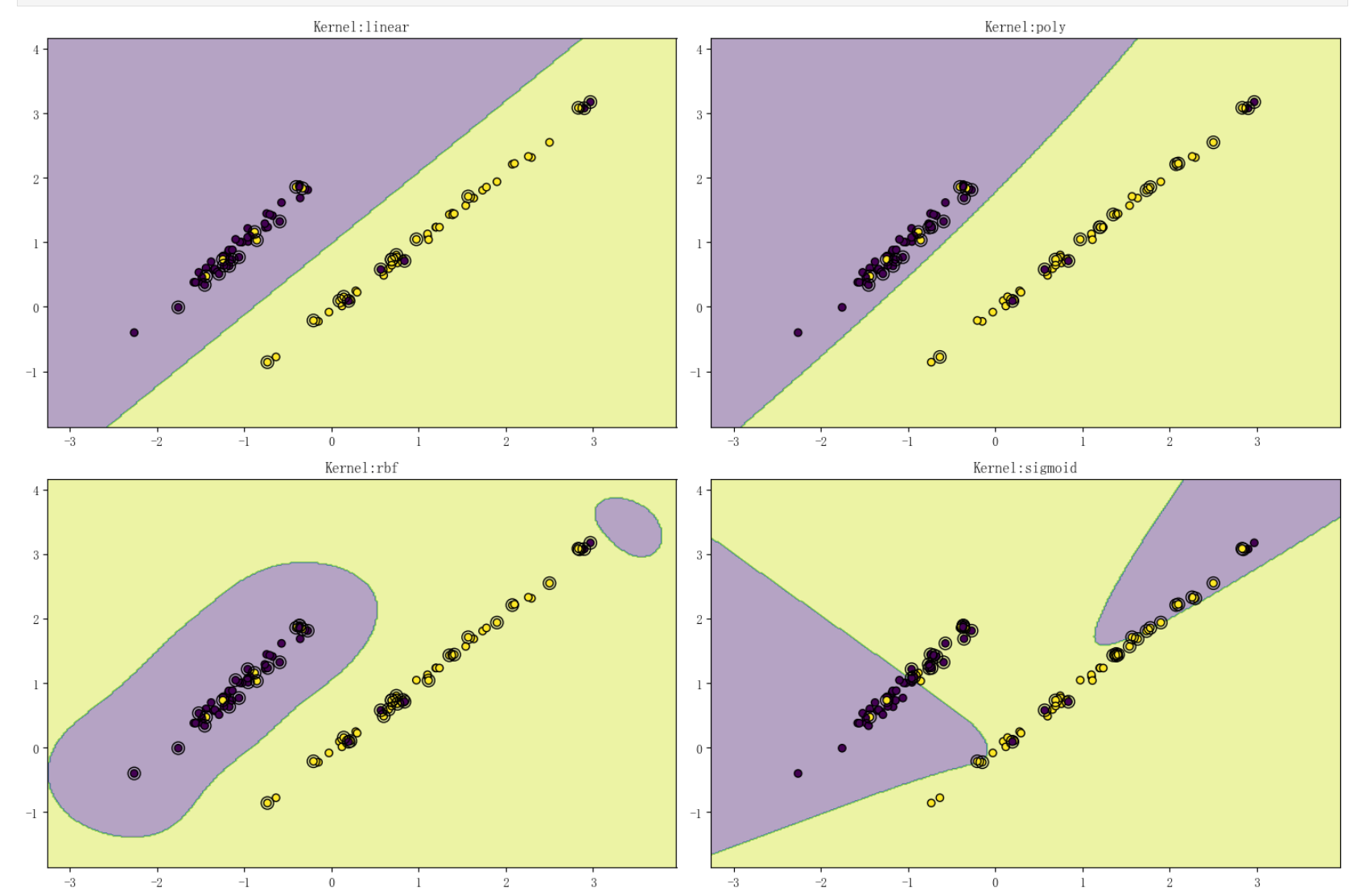
2.3核函数性能对比
| 核函数 | 适用场景 | 数学形式 | 参数说明 |
|---|---|---|---|
| 线性核 | 线性可分 | ( K(x,y) = x*y ) | 无额外参数 |
| 多项式核 | 适度非线性 | ( K(x,y) = ( | ( |
| RBF核 | 复杂非线性 | ( K(x,y) = | ( |
| Sigmoid核 | 神经网络式 | ( K(x,y) = | ( |
核函数选择示例
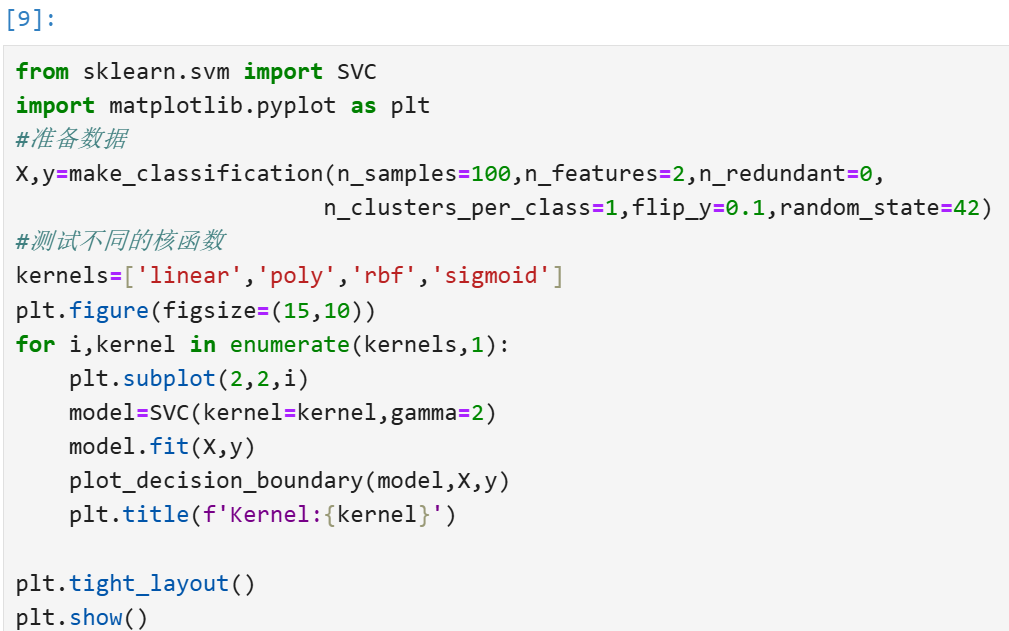
2.4参数调优

参数影响范围:
-C值:控制间隔宽度与分类错误的权衡
-C↑→间隔↓→可能过拟合
-C↓→间隔↑→可能欠拟合
-gamma值:控制单个样本影响力
-gamma↑→决策边界更复杂
-gamma↓→决策边界更平滑
3.决策树与随机森林
3.1决策树
决策树是一种基于树形结构的监督学习算法,通过递归地划分特征空间实现分类或回归。其核心组件包括:
-根节点:包含完整数据集的最顶层节点
-内部节点:表示特征测试条件
-分支:对应特征测试结果
-叶节点:存储最终预测结果
训练伪代码:
from sklearn.tree import DecisionTreeClassifier,export_text
#示例:构建决策树分类器
"""
参数详解:
criterion='gini':使用基尼不纯度作为分裂标准(替代选项'entropy')
max_depth=3:限制树的最大深度防止过拟合
min_samples_split=5:节点至少包含5个样本才允许继续分裂
min_samples_leaf=2:叶节点至少包含2个样本
random_state=42:固定随机种子保证可复现性
"""
dt=DecisionTreeClassifier(
criterion='gini',
max_depth=3,
min_samples_split=5,
min_samples_leaf=2,
random_state=42
)
#训练过程(伪代码)
defbuild_tree(data):
if所有样本属于同一类别or达到停止条件:
创建叶节点(返回类别标签/回归值)
return
选择最优分裂特征和分割点#基于不纯度减少最大化
将数据划分为左右子集
left_subtree=build_tree(左子集)
right_subtree=build_tree(右子集)
return决策节点(feature,threshold,left_subtree,right_subtree)
核心部分伪代码:
def build_decision_tree(data,current_depth=0):
#停止条件判断
if all_samples_same_class(data)orcurrent_depth>=max_depthorlen(data)<min_samples_split:
leaf_value=calculate_leaf_value(data)#返回多数类别或平均值
return LeafNode(leaf_value)
#寻找最佳分裂
best_split=find_best_split(data)
if best_split.gain<min_gain_threshold:#增益不足则停止
leaf_value=calculate_leaf_value(data)
returnLeafNode(leaf_value)
#递归构建子树
left_subtree=build_decision_tree(best_split.left_data,current_depth+1)
right_subtree=build_decision_tree(best_split.right_data,current_depth+1)
return DecisionNode(
feature_index=best_split.feature_index,
threshold=best_split.threshold,
left=left_subtree,
right=right_subtree
)
def find_best_split(data):
best_gain=-float('inf')
best_split=None
#遍历所有特征
for feature_idx in range(n_features):
#遍历所有可能的分割点
for threshold in get_possible_thresholds(data,feature_idx):
left_data,right_data=split_data(data,feature_idx,threshold)
#计算信息增益
current_gain=information_gain(data,left_data,right_data)
if current_gain>best_gain:
best_gain=current_gain
best_split=SplitResult(
feature_index=feature_idx,
threshold=threshold,
gain=current_gain,
left_data=left_data,
right_data=right_data
)
return best_split

3.2随机森林
集成学习原理
随机森林属于Bagging类集成方法,通过构建多棵决策树并聚合预测结果提升模型性能。其核心机制包括:
Bootstrap采样:每棵树使用不同的数据子集(有放回抽样)
-特征随机性:每个节点分裂时仅考虑随机特征子集
-投票机制:分类任务采用多数表决,回归任务取平均值
随机森林学习伪代码:
from sklearn.ensemble import RandomForestClassifier
#示例:构建随机森林
"""
参数详解:
n_estimators=100:森林中树的数量
max_features='sqrt':每次分裂考虑√n_features个特征
bootstrap=True:启用Bootstrap采样
oob_score=True:计算袋外估计准确率
max_samples=0.8:每棵树使用80%的样本
"""
rf=RandomForestClassifier(
n_estimators=100,
criterion='gini',
max_depth=None,#不限制单棵树深度
min_samples_split=2,
min_samples_leaf=1,
max_features='sqrt',
bootstrap=True,
oob_score=True,
max_samples=0.8,
random_state=42,
n_jobs=-1#使用所有CPU核心
)
#训练过程(伪代码)
def train_rf():
forest=[]
for i in range(n_estimators):
#1.Bootstrap采样
X_sample,y_sample=bootstrap_sample(X_train,y_train)
#2.构建决策树(考虑特征子集)
tree=build_tree_with_feature_sampling(X_sample,y_sample)
forest.append(tree)
return forest
def predict_rf(forest,X):
predictions=[]
for tree in forest:
predictions.append(tree.predict(X))
return majority_vote(predictions)#分类任务
RandomForest详解:
classRandomForest:
def __init__(self,n_trees=100,max_features='sqrt'):
self.n_trees=n_trees
self.max_features=max_features
self.trees=[]
def fit(self,X,y):
self.trees=[]
n_features=X.shape[1]
#确定每棵树使用的特征数
if self.max_features=='sqrt':
max_features=int(np.sqrt(n_features))
elif self.max_features=='log2':
max_features=int(np.log2(n_features))
else:
max_features=self.max_features
#构建多棵决策树
for _ in range(self.n_trees):
#Bootstrap采样
sample_indices=np.random.choice(len(X),size=len(X),replace=True)
X_sample,y_sample=X[sample_indices],y[sample_indices]
#随机选择特征子集
feature_indices=np.random.choice(
n_features,
size=max_features,
replace=False
)
X_sample=X_sample[:,feature_indices]
#构建决策树
tree=DecisionTree().fit(X_sample,y_sample)
self.trees.append((tree,feature_indices))
def predict(self,X):
all_preds=[]
for tree,feature_indices in self.trees:
X_subset=X[:,feature_indices]
pred=tree.predict(X_subset)
all_preds.append(pred)
#多数表决(分类)或平均(回归)
return mode(all_preds,axis=0)[0][0]



3.3两种学习算法对比
以下是决策树与随机森林的特性对比表格:
| 特性 | 决策树 | 随机森林 |
|---|---|---|
| 模型复杂度 | 低(单模型) | 高(多模型集成) |
| 方差 | 高(易过拟合) | 低(方差减少) |
| 偏差 | 低 | 中等 |
| 训练速度 | 快 | 慢(与树数量线性相关) |
| 预测速度 | 极快 | 中等 |
| 可解释性 | 强(可可视化) | 弱 |
| 参数敏感性 | 高 | 低 |
| 数据需求 | 小样本有效 | 需要足够数据 |
| 缺失值处理 | 天然支持 | 需要额外处理 |
决策树分裂标准
基尼(Gini)不纯度(GiniImpurity):
信息增益(熵):
分裂算法:
CART算法(ClassificationAndRegressionTrees)采用二元递归分裂:
随机森林多样性保障
-特征子集大小:通常取总特征数的平方根
-袋外误差:
泛化误差上界:
3.4两种算法进阶用法
决策树剪枝示例:
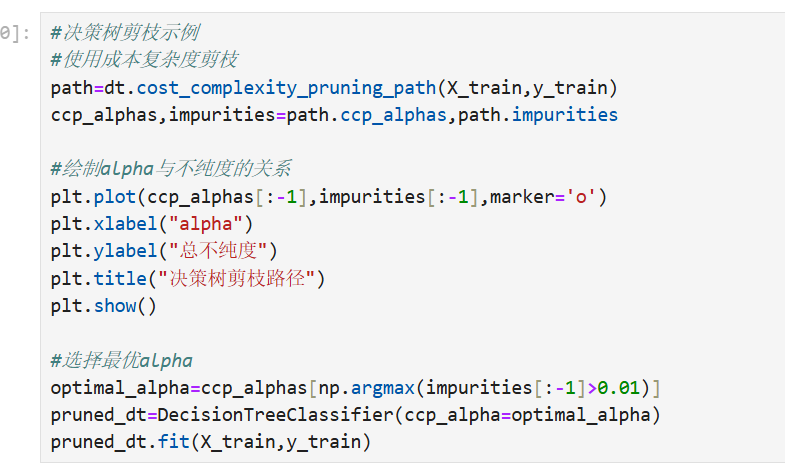
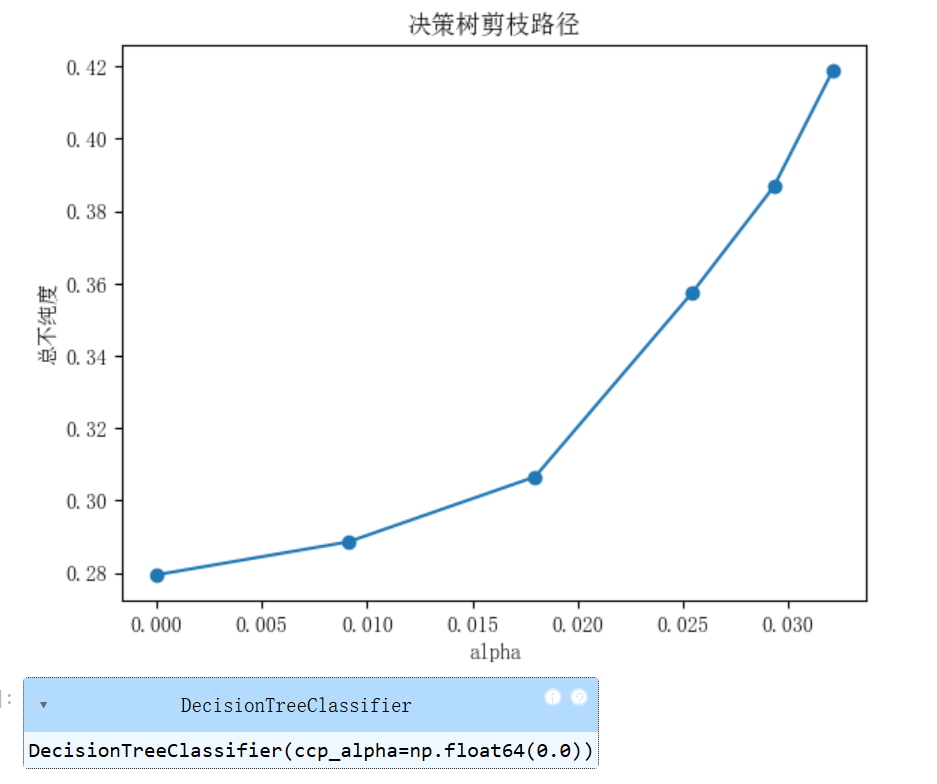
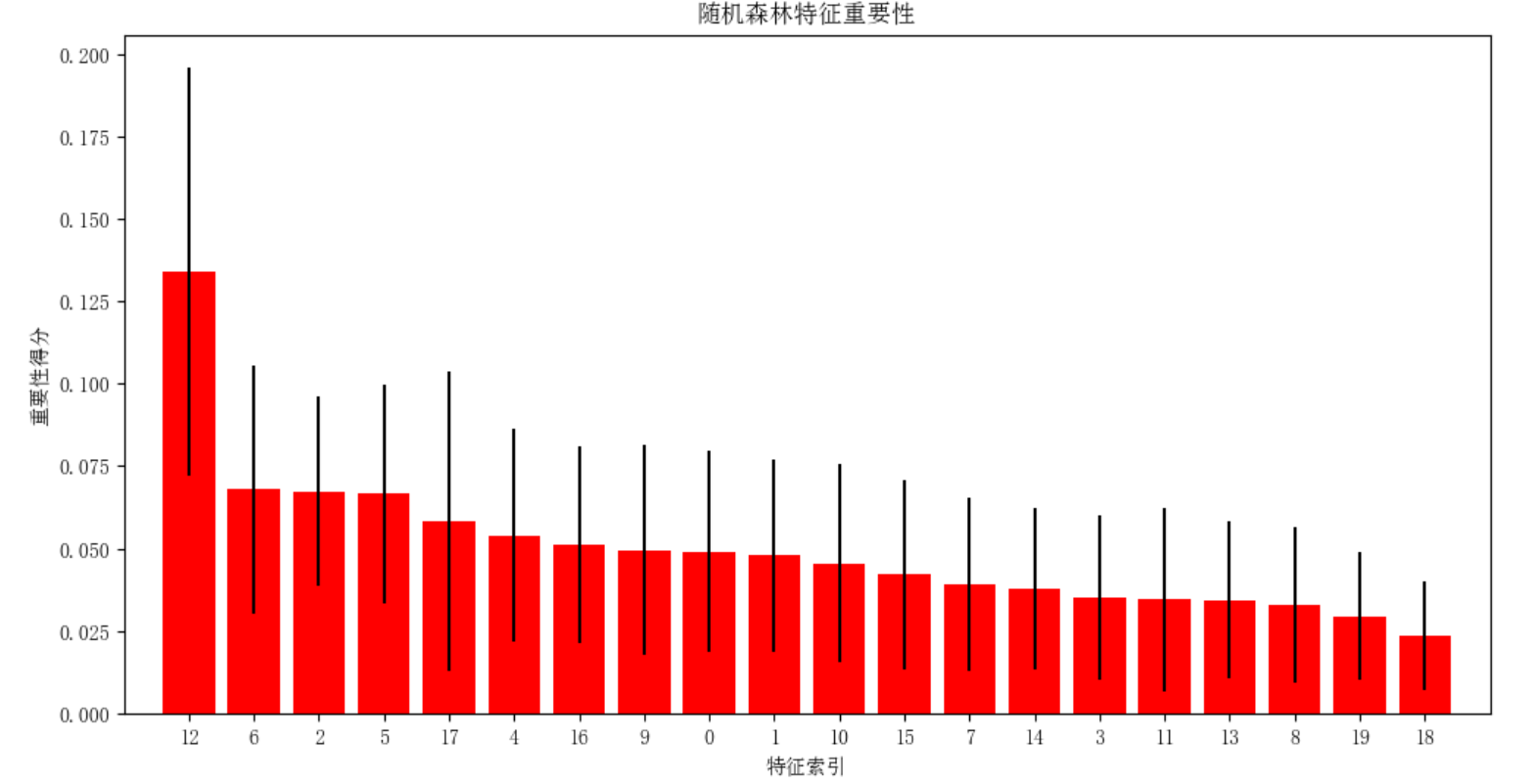
随机森林特征选择:
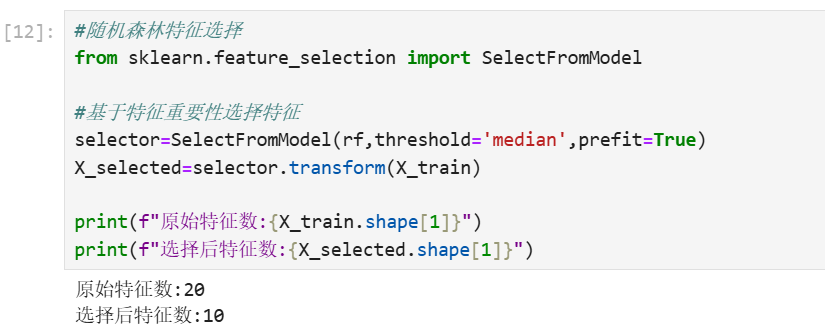
4.k-近邻算法(KNN)
4.1基本概念
KNN是一种基于实例的监督学习算法,其核心思想是"物以类聚"。预测新样本时,通过其K个最近邻样本的类别(分类)或值(回归)来决定预测结果。
关键要素:
-K值:考虑的最近邻数量
-距离度量:计算样本相似度的标准(欧氏/曼哈顿/余弦等)
-决策规则:分类常用多数表决,回归常用平均值
算法流程伪代码:
def knn_predict(X_train,y_train,X_new,k=5,metric='euclidean'):
#1.计算X_new与所有训练样本的距离
distances=[]
for i,x in enumerate(X_train):
dist=calculate_distance(xi,X_new,metric)
distances.append((dist,y_train[i]))
#2.按距离排序并选择K个最近邻
distances.sort(key=lambda x:x[0])
neighbors=[y for dist,y in distances[:k]]
#3.应用决策规则
if is_classification:
return mode(neighbors)#多数表决
else:
return mean(neighbors)#平均值
4.2分类任务和回归任务
分类任务实现:
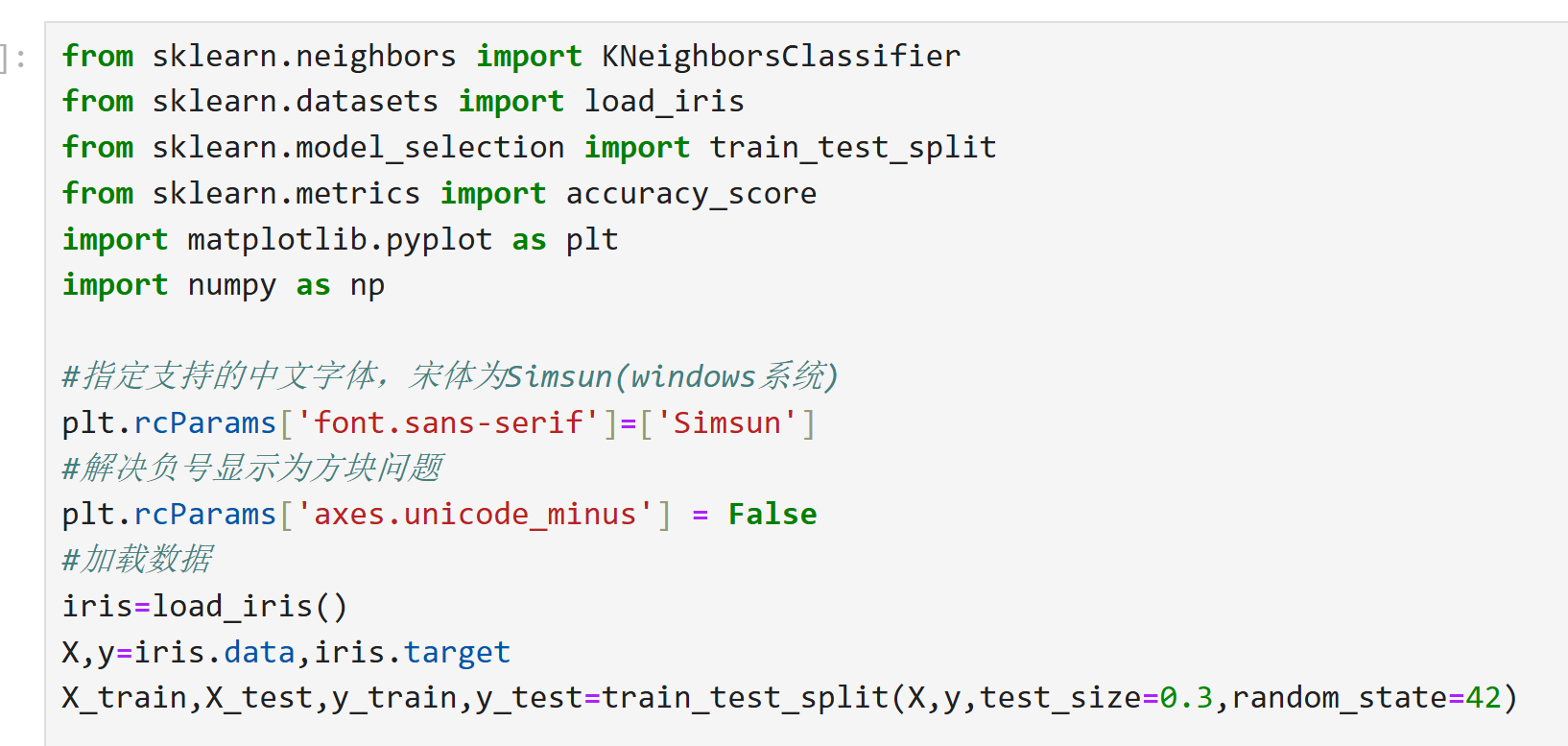

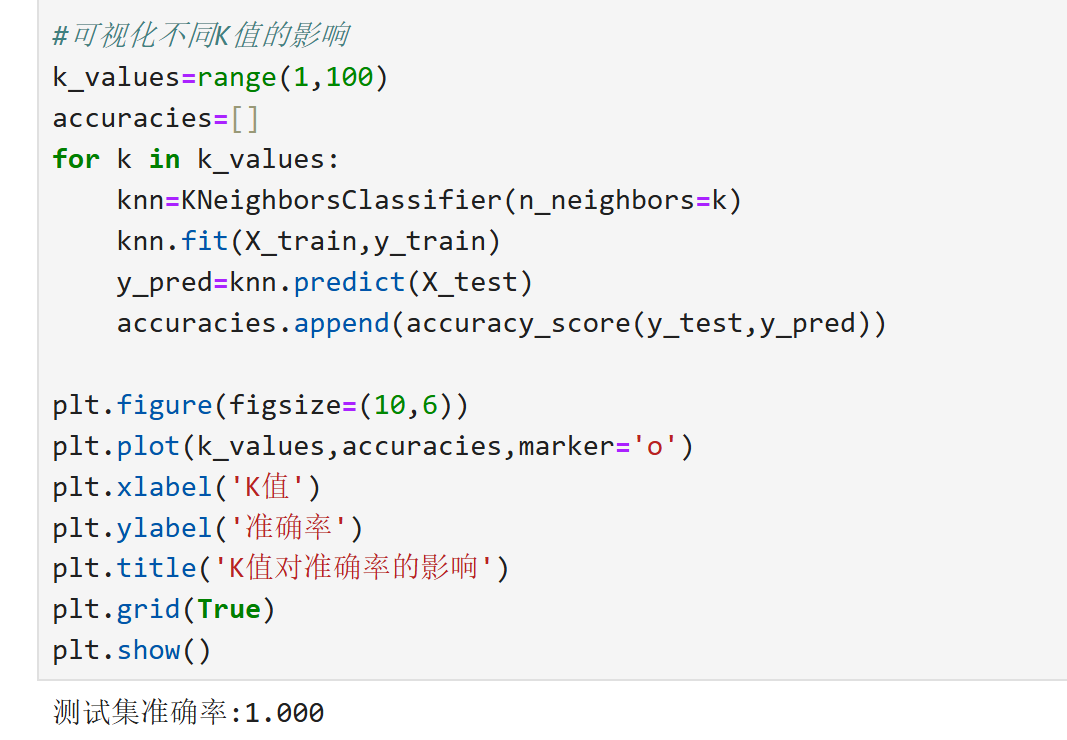
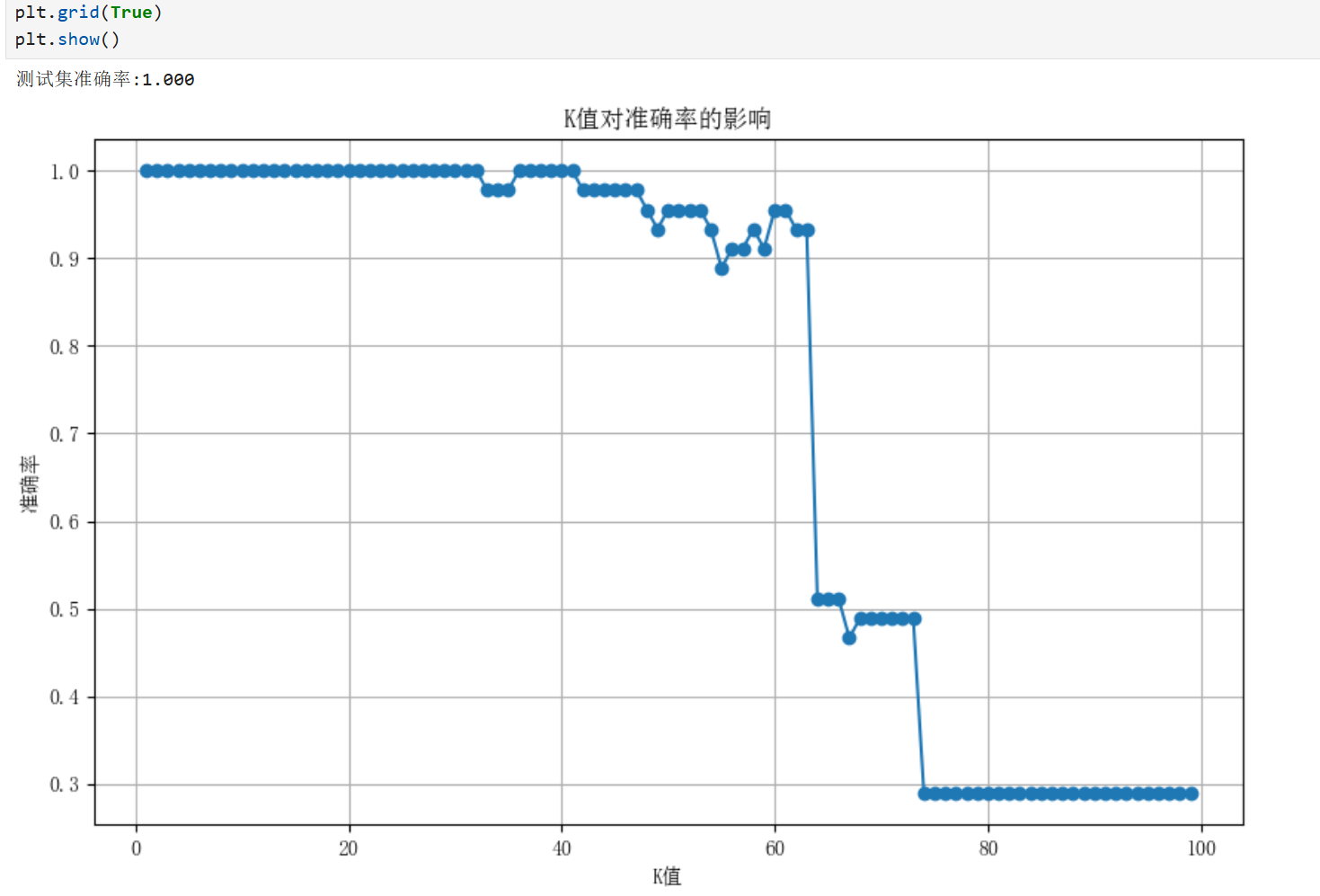
回归任务实现:
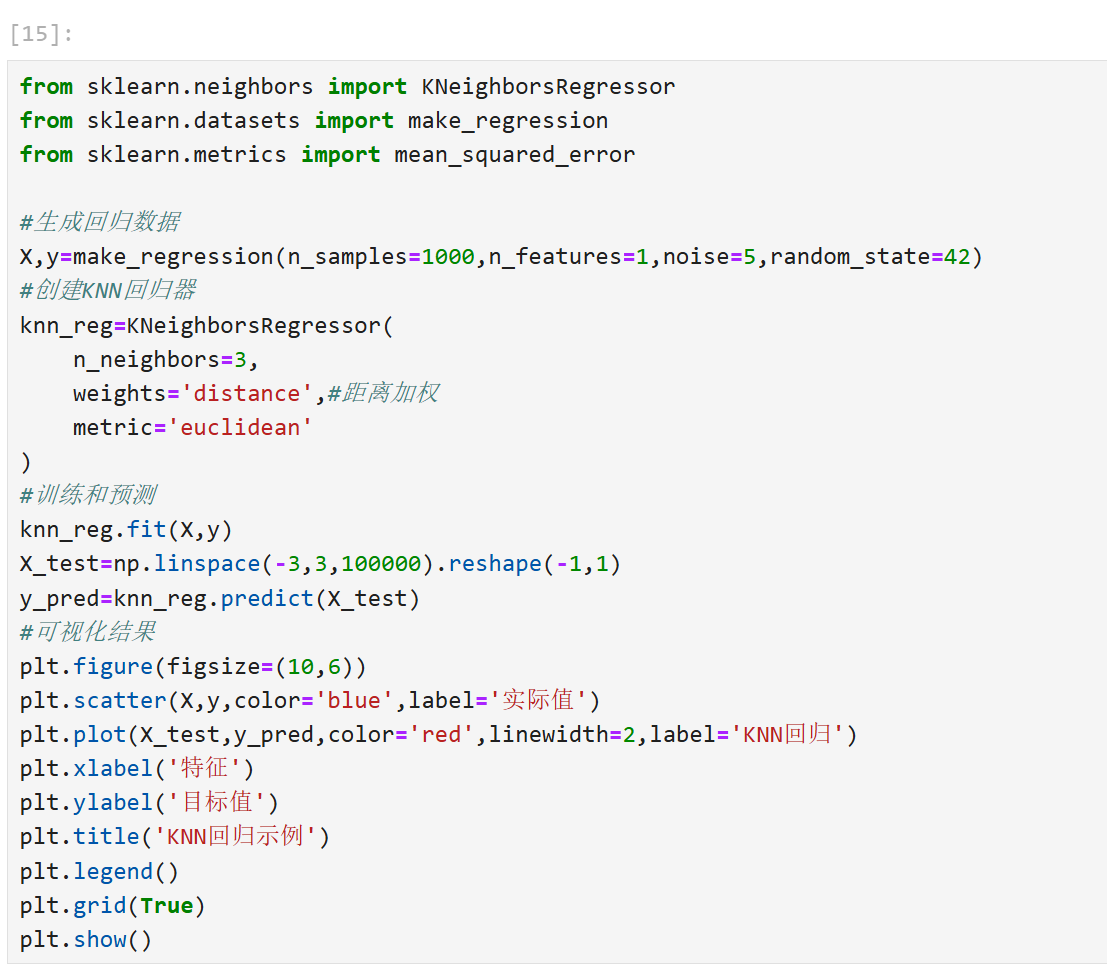
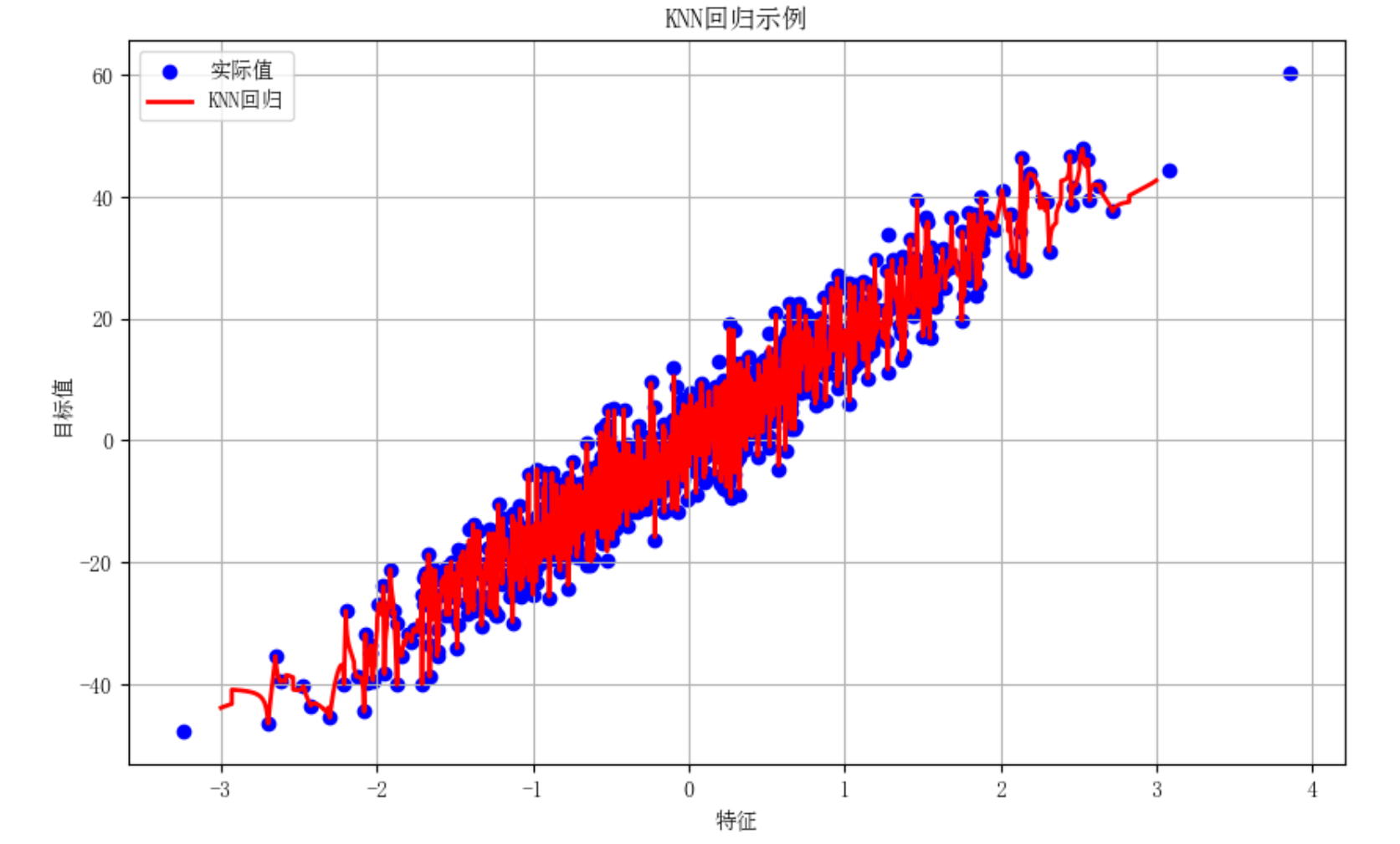
4.3常用数学公式和参数分析
欧式距离:d(x,y)=
曼哈顿距离:
闵可夫斯基距离(通用形式):
余弦相似度:
KNN参数优化指南
| 参数 | 影响 | 推荐值 |
|---|---|---|
| n_neighbors | K值增大会使决策边界更平滑 | 3-20(通过交叉验证选择最佳值) |
| weights | 'distance'给近邻更大权重 | 数据不平衡时建议使用'distance' |
| metric | 影响最近邻的选择方式 | 数值型数据建议使用'euclidean'(欧氏距离) |
| p | 控制闵可夫斯基距离的计算方式 | p=1(曼哈顿距离),p=2(欧氏距离) |
注:实际应用中需结合具体数据集特点进行调整,交叉验证是确定最佳参数的有效方法。
5.朴素贝叶斯
5.1基本概念
朴素贝叶斯是基于贝叶斯定理与特征条件独立假设的分类方法。"朴素"体现在假设所有特征之间相互独立,虽然现实中很难满足,但实际表现往往很好。
贝叶斯定理:
三种常见变体
1.高斯朴素贝叶斯:假设连续特征服从正态分布
2.多项式朴素贝叶斯:适用于离散特征(如文本分类的词频)
3.伯努利朴素贝叶斯:适用于二元特征(如文本分类的单词出现与否)
5.2贝叶斯代码
高斯朴素贝叶斯:

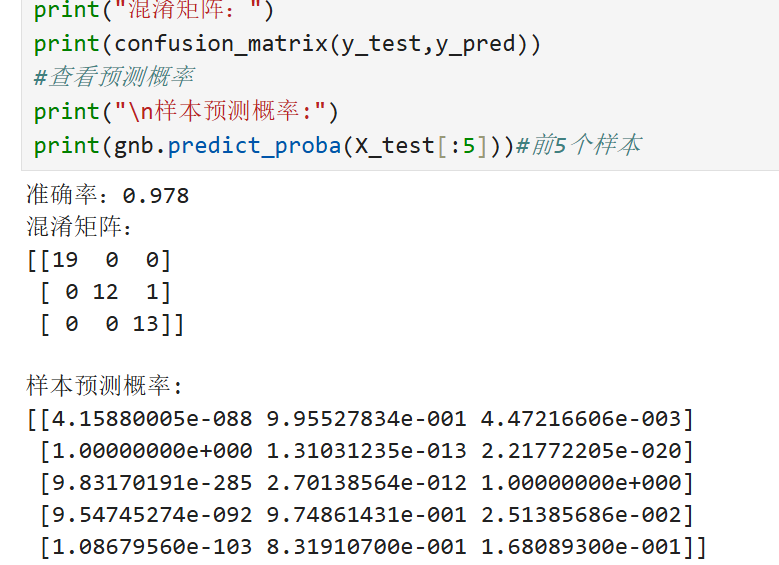
多项式朴素贝叶斯(文本分类示例):

5.3数学推导
1.分类决策规则:对于输入特征向量x=(x₁,x₂,...,xₙ),选择使后验概率最大的类别:
2.高斯分布参数估计:对第j个特征和第k个类别:
3.平滑处理:拉普拉斯平滑(多项式分布):
朴素贝叶斯与逻辑回归对比
| 特性 | 朴素贝叶斯 | 逻辑回归 |
|---|---|---|
| 模型类型 | 生成模型 | 判别模型 |
| 假设条件 | 特征独立 | 无强假设 |
| 参数估计 | 最大似然 | 最大似然/正则化 |
| 处理高维 | 更适合 | 需要正则化 |
| 计算效率 | 更高 | 较低 |
表格内容清晰展示了两种算法在模型类型、假设条件等关键维度上的差异。
四、无监督学习算法
1.K-means
1.1基本概念
K-means是一种基于距离的划分聚类方法,通过迭代将数据划分为K个簇。其核心思想是最小化簇内平方和(WCSS):
其中:
-k:预设的簇数量
-C_i:第i个簇
-μ_i:第i个簇的质心
算法流程
1.随机初始化K个质心
2.将每个样本分配到最近的质心形成簇
3.重新计算每个簇的质心
4.重复2-3步直到质心不再变化或达到最大迭代次数
1.2代码实践
基本实现:

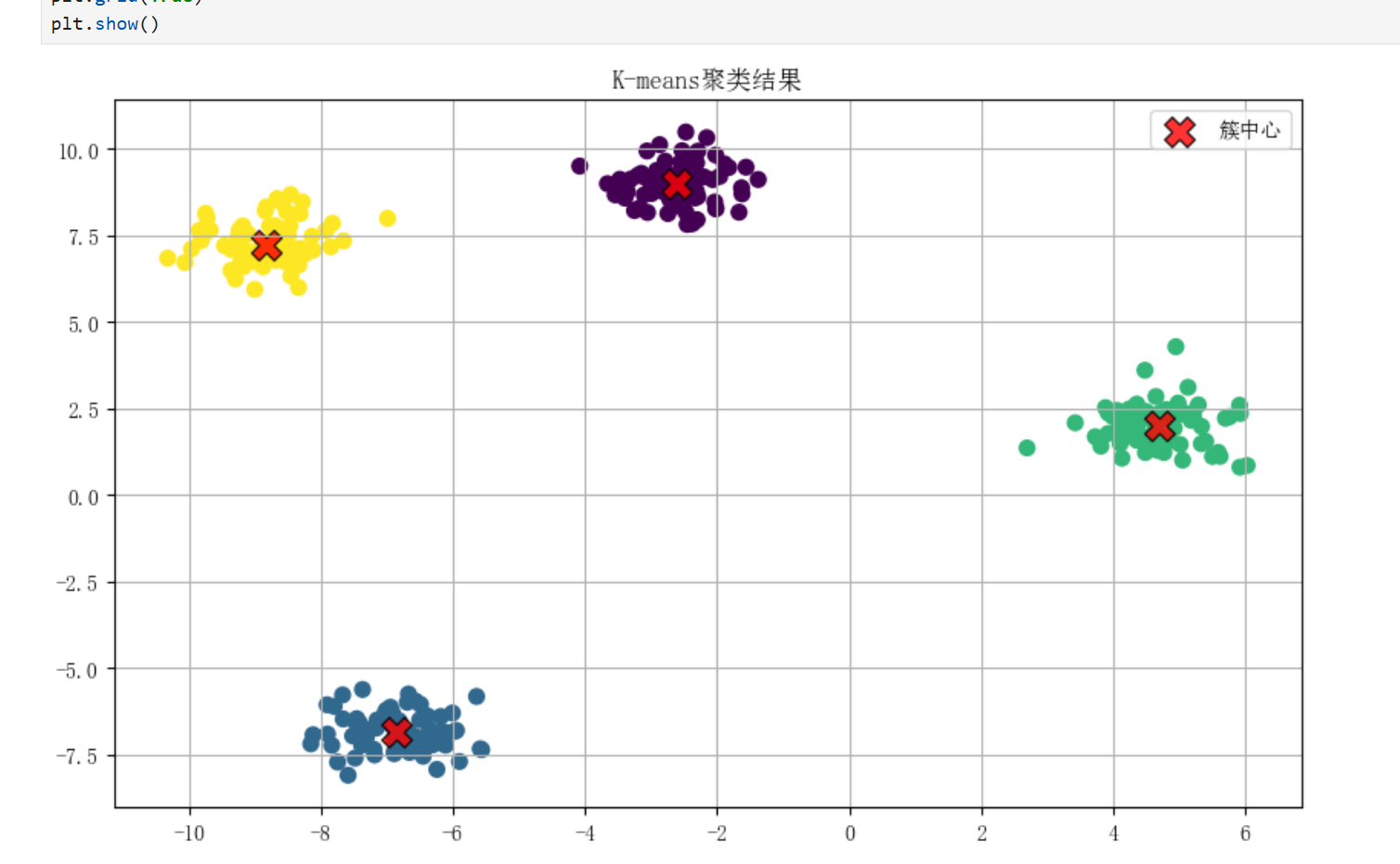
肘部法则确定K值:
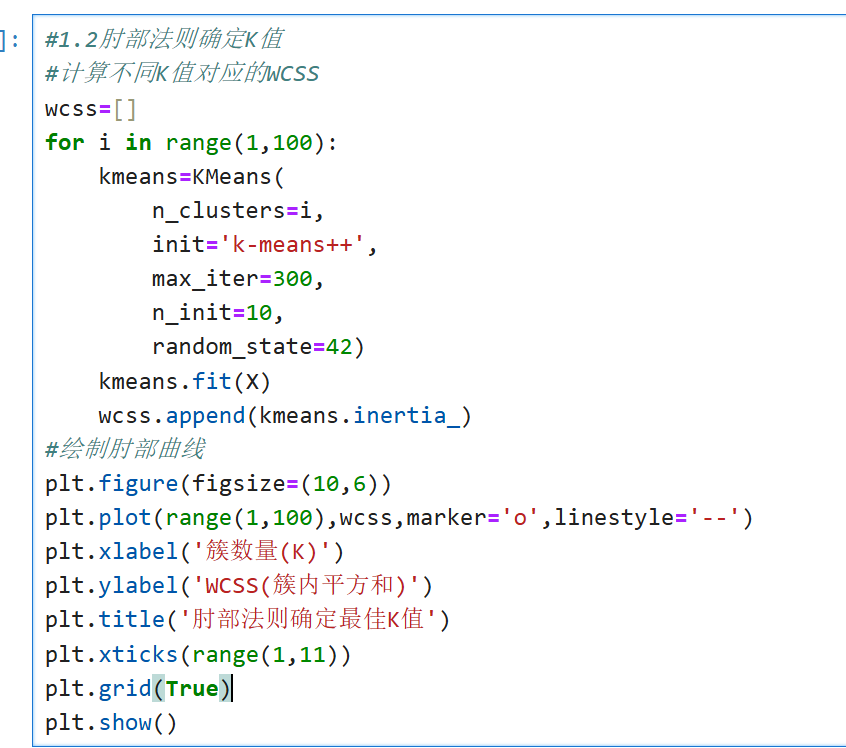
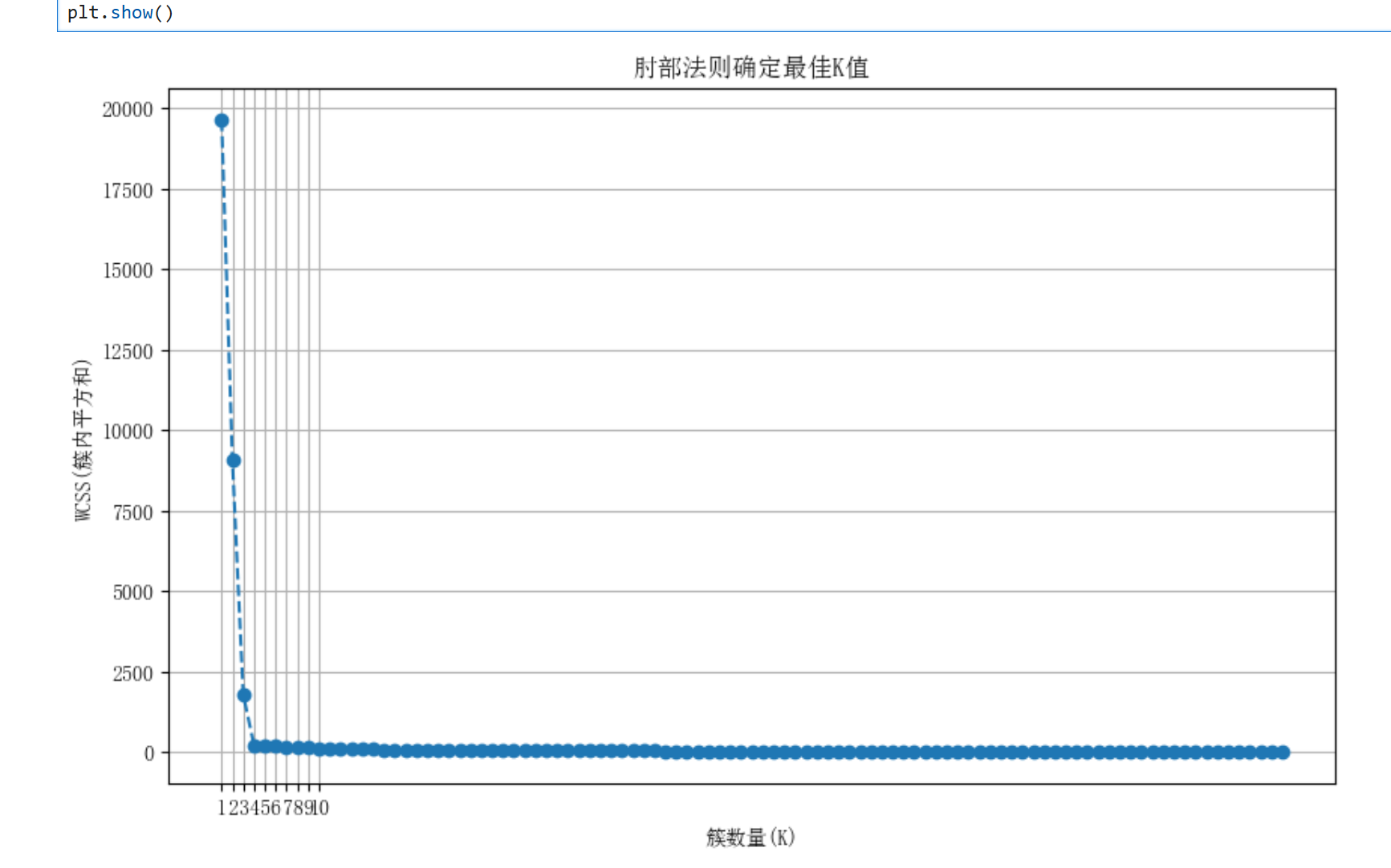
1.3数学推导
K-means优化问题可形式化为:
其中μ_i是簇C_i的均值向量:
K-means保证在有限步内收敛,因为:
1.样本分配步骤使WCSS不增加
2.质心更新步骤使WCSS不增加
3.WCSS有下界0
优点:
-简单高效,计算复杂度O(nkdi)
-适合规则形状、密度均匀的簇
-可扩展到大样本集(mini-batch变体)
缺点:
-需要预先指定K值
-对初始质心敏感
-对噪声和离群点敏感
-不适合非凸形状的簇
以下是K-means与层次聚类的对比表格:
| 特性 | K-means | 层次聚类 |
|---|---|---|
| 计算复杂度 | 低 | 高 |
| 需要K值 | 是 | 否 |
| 结果稳定性 | 较低 | 较高 |
| 适合数据量 | 大规模 | 小规模 |
| 可视化 | 直接 | 树状图 |
2.层次聚类
2.1基本概念
层次聚类通过构建树状图(Dendrogram)来形成数据集的层次分解,主要分为两种策略:
凝聚法(Agglomerative):自底向上,每个样本初始为一簇,逐步合并。
分裂法(Divisive):自顶向下,所有样本初始为一簇,逐步分裂。
关键要素:
连接准则(Linkage Criteria):
单连接(Single):最小距离
全连接(Complete):最大距离
平均连接(Average):平均距离
沃德法(Ward):最小化方差增加
距离度量:欧氏距离(默认)、曼哈顿距离、余弦距离等
2.2完整代码实现
凝聚层次聚类
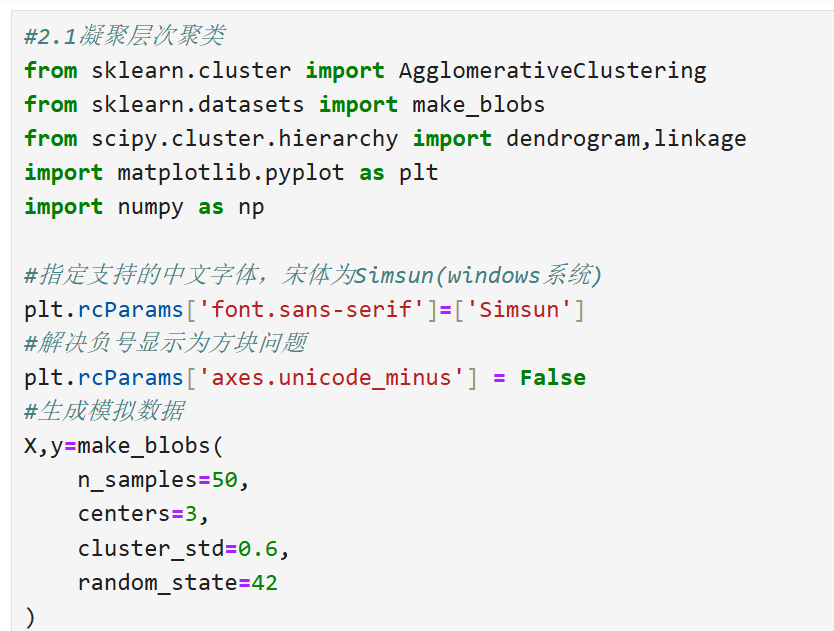

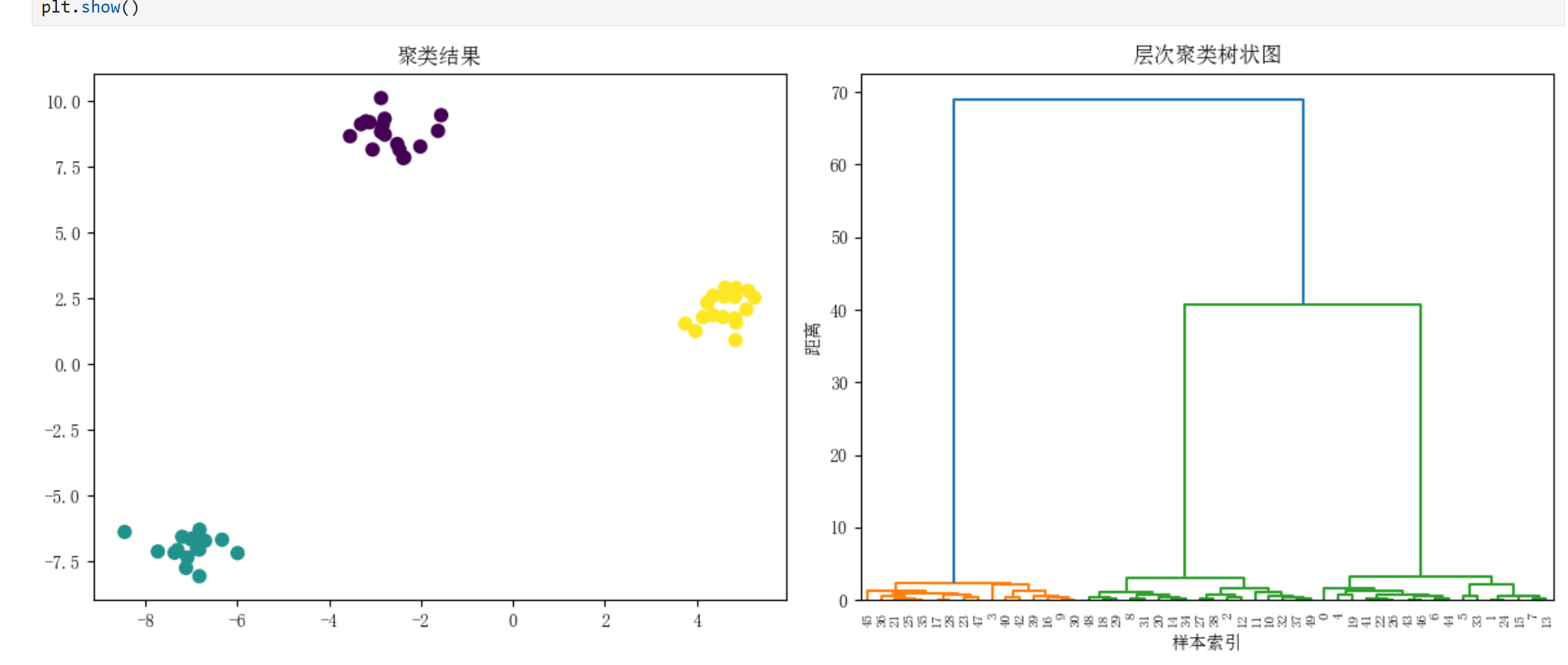
不同连接准则对比

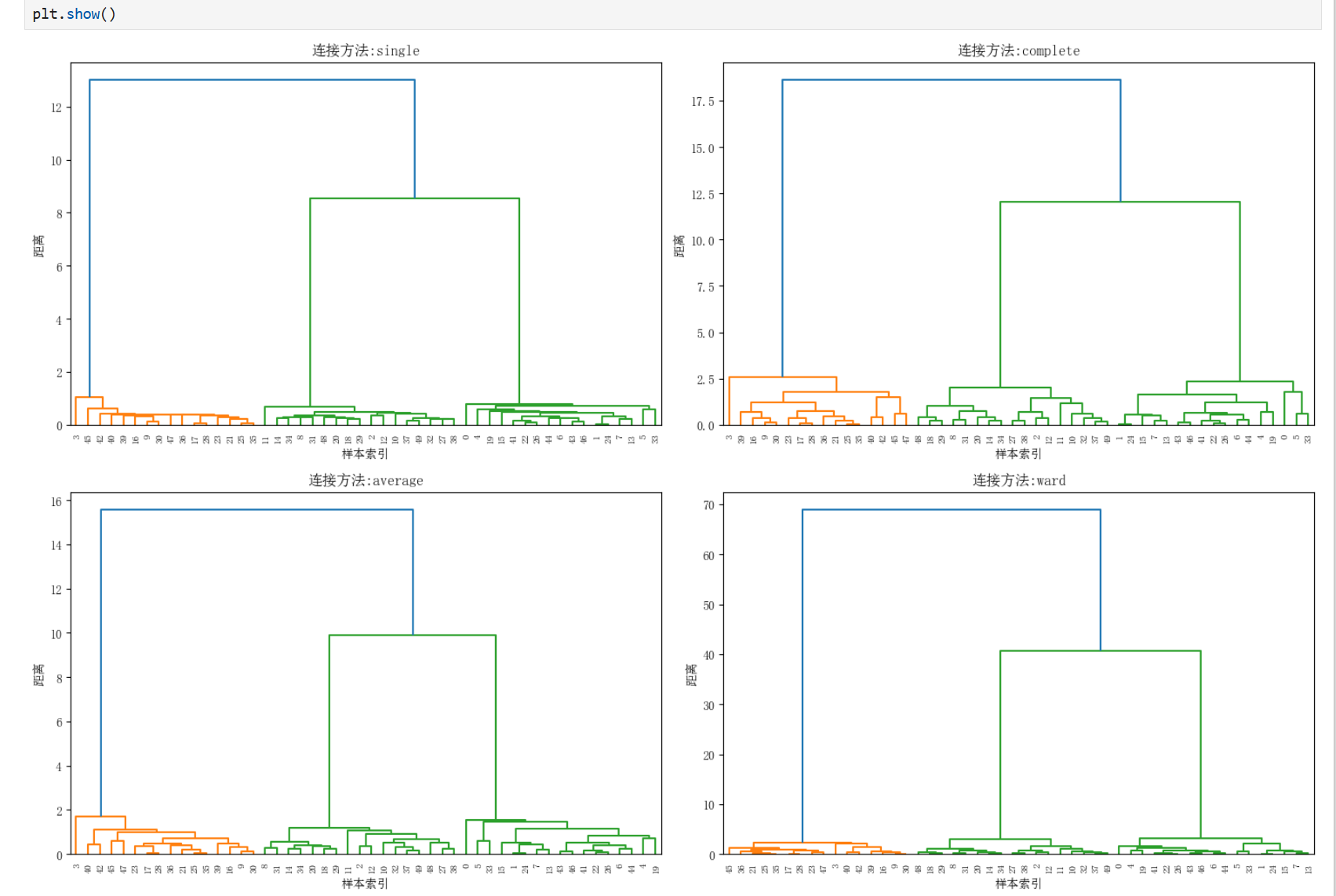
2.3数学推导
1.单连接
2.全连接
3.平均连接
4.沃德法
以下是根据要求整理的算法复杂度表格:
算法复杂度对比
| 算法类型 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 凝聚法 | O(n³) | O(n²) |
| 分裂法 | O(2ⁿ) | O(n²) |
优点:
不需要预先指定簇数
树状图提供直观的层次关系
对距离度量选择不敏感(相比K-means)
可以发现任意形状的簇
缺点:
计算复杂度高,不适合大数据集
对噪声和离群点敏感
一旦样本被分配不能更改
分裂法计算代价极高
结合热力图分析:
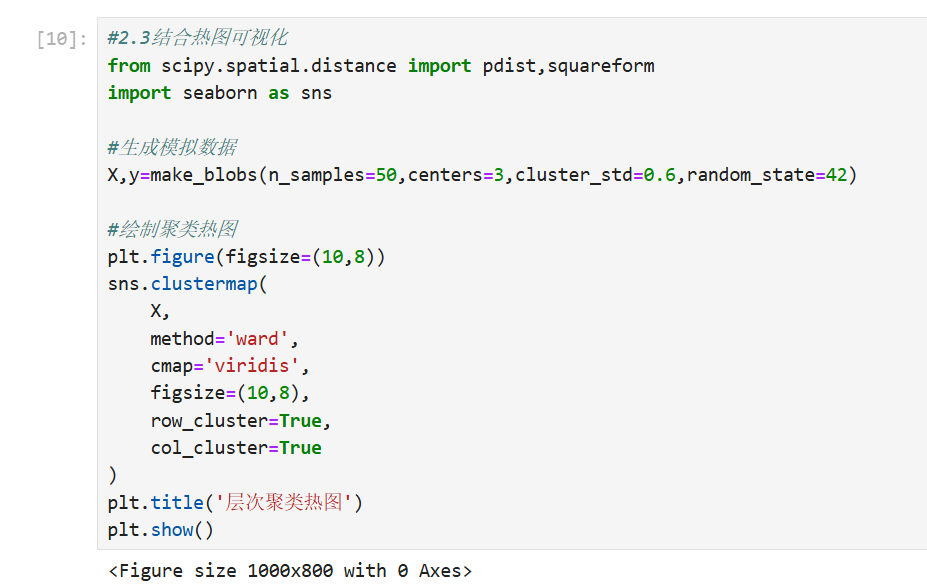
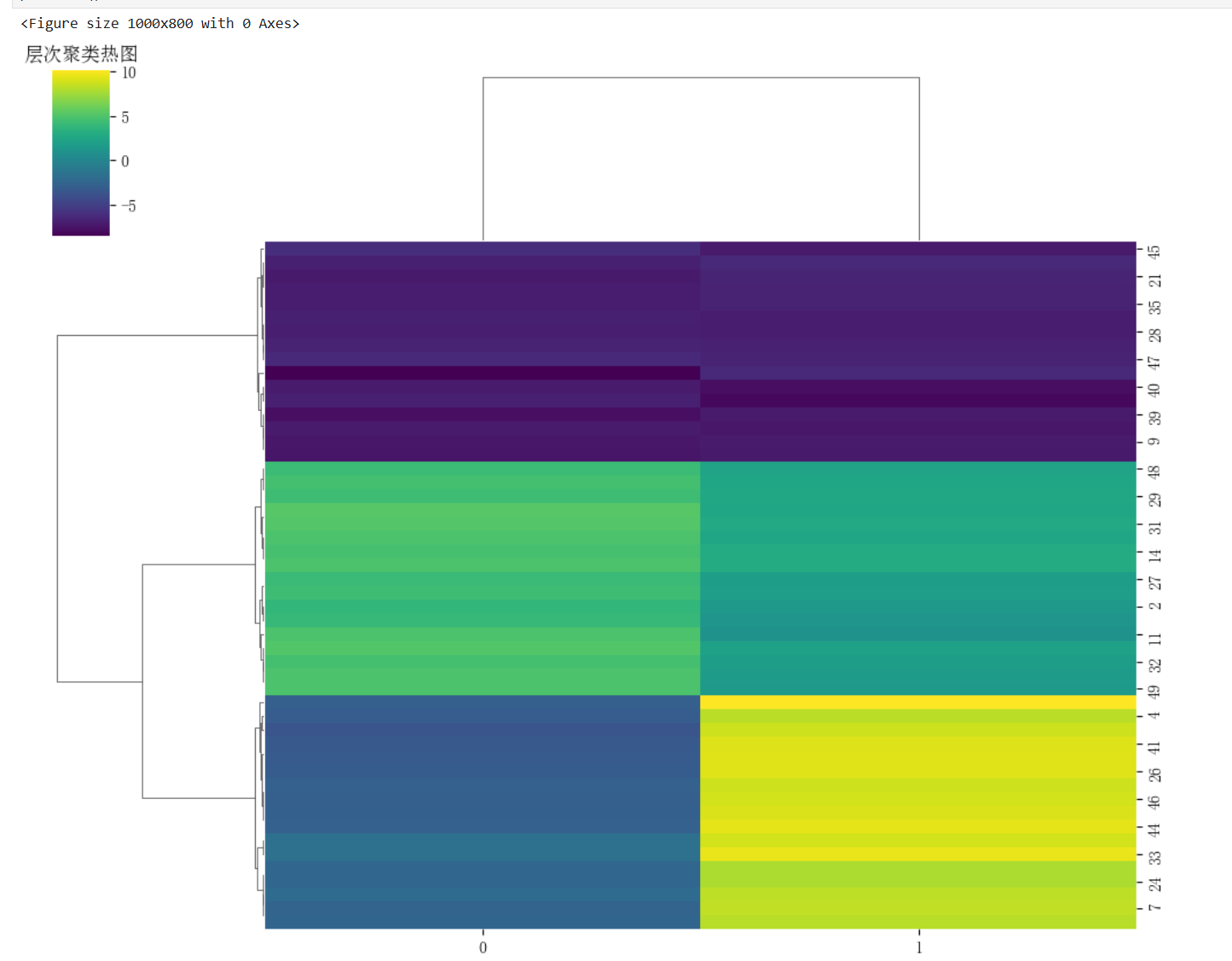
3.主成分分析(PCA)
3.1基本概念
PCA是一种线性降维技术,通过正交变换将原始特征空间重构为新的正交基空间,其核心目标是:
最大化方差保留:寻找数据变异最大的方向作为主成分轴
消除特征相关性:转换后的新特征(主成分)彼此线性无关
实现维度压缩:用少数主成分解释大部分数据变异
主成分分析(Principal Component Analysis)是一种通过正交变换将一组可能存在相关性的变量转换为一组线性不相关变量的统计方法。转换后的变量称为主成分,按方差大小排序。
核心思想:
方差最大化:保留数据最大变异方向
维度缩减:用少数主成分解释大部分方差
去相关性:转换后的特征线性无关
算法变体
以下是基于输入信息整理的PCA变体及其核心改进和适用场景的表格:
| 变体名称 | 核心改进 | 适用场景 |
|---|---|---|
| 核 PCA (Kernel PCA) | 通过核函数处理非线性 | 非线性数据结构 |
| 稀疏 PCA (Sparse PCA) | 引入 L1 正则化增强稀疏性 | 高维特征选择 |
| 增量 PCA (Incremental PCA) | 支持分批处理数据 | 大规模数据集 |
| 鲁棒 PCA (Robust PCA) | 抵抗异常值或噪声干扰 | 含噪声或异常值的数据 |
关键说明
- 核 PCA:利用核技巧(如高斯核、多项式核)将数据映射到高维空间,解决线性不可分问题。
- 稀疏 PCA:通过 L1 正则化约束载荷矩阵,产生稀疏性,便于特征解释和降维。
- 增量 PCA:逐批次更新模型参数,避免一次性加载全部数据,节省内存。
- 鲁棒 PCA:将数据分解为低秩矩阵(主成分)和稀疏矩阵(噪声/异常值),提高稳定性。
与其他降维方法对比
以下是整理后的对比表格,清晰展示PCA、t-SNE、LDA和自编码器的关键特性差异:
| 特性 | PCA | t-SNE | LDA | 自编码器 |
|---|---|---|---|---|
| 监督性 | 无监督 | 无监督 | 有监督 | 无监督 |
| 保持结构 | 全局 | 局部 | 类别间 | 可调节 |
| 计算复杂度 | O(p³) | O(n²) | O(p³) | 依赖网络 |
| 可解释性 | 高 | 低 | 中 | 低 |
| 参数敏感性 | 低 | 高 | 中 | 高 |
关键说明
- 监督性:LDA需要标签信息指导降维,其他方法无需标签。
- 结构保持:PCA保留全局方差,t-SNE侧重局部邻域结构,LDA最大化类间分离。
- 复杂度:PCA和LDA依赖特征维度$p$的立方,t-SNE随样本量$n$平方增长,自编码器依赖网络结构。
- 参数敏感性:t-SNE需调试困惑度等参数,自编码器对网络架构敏感。
3.2代码实现
基本PCA实现

手动实现PCA

确定最佳主成分数

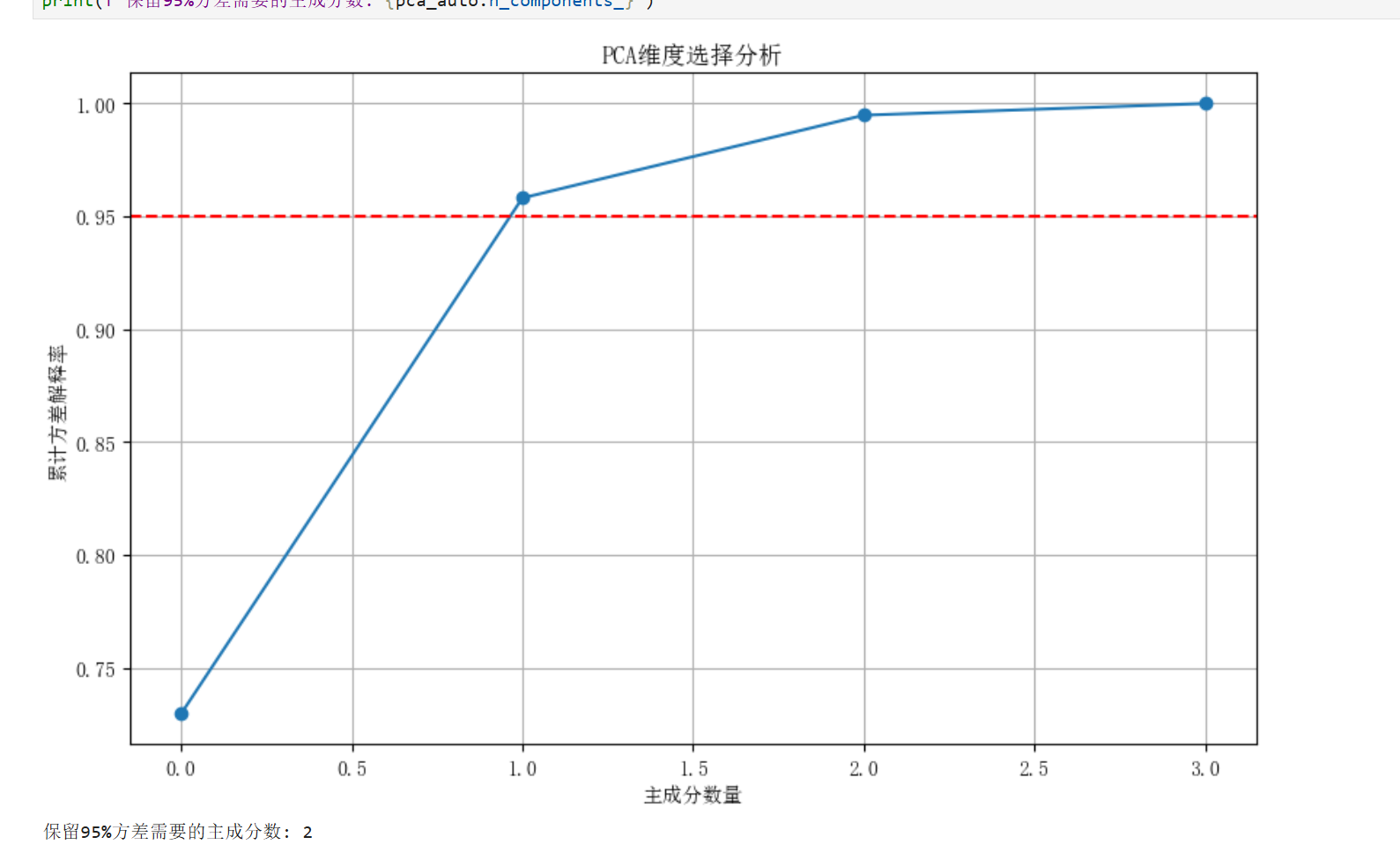
主成分分析报告
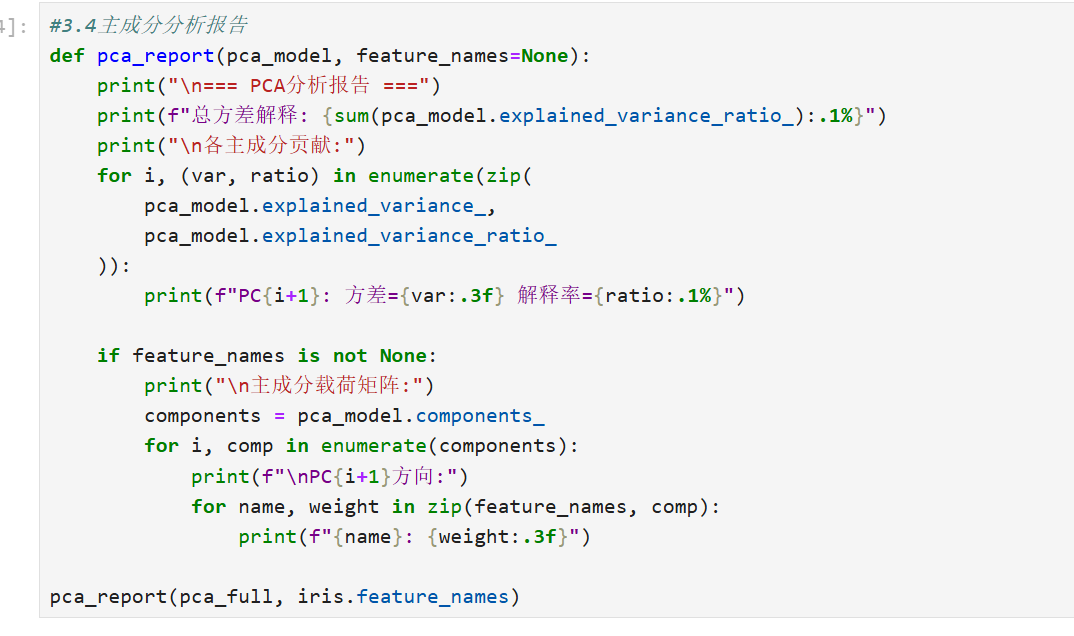

工业级PCA实现(带异常处理)

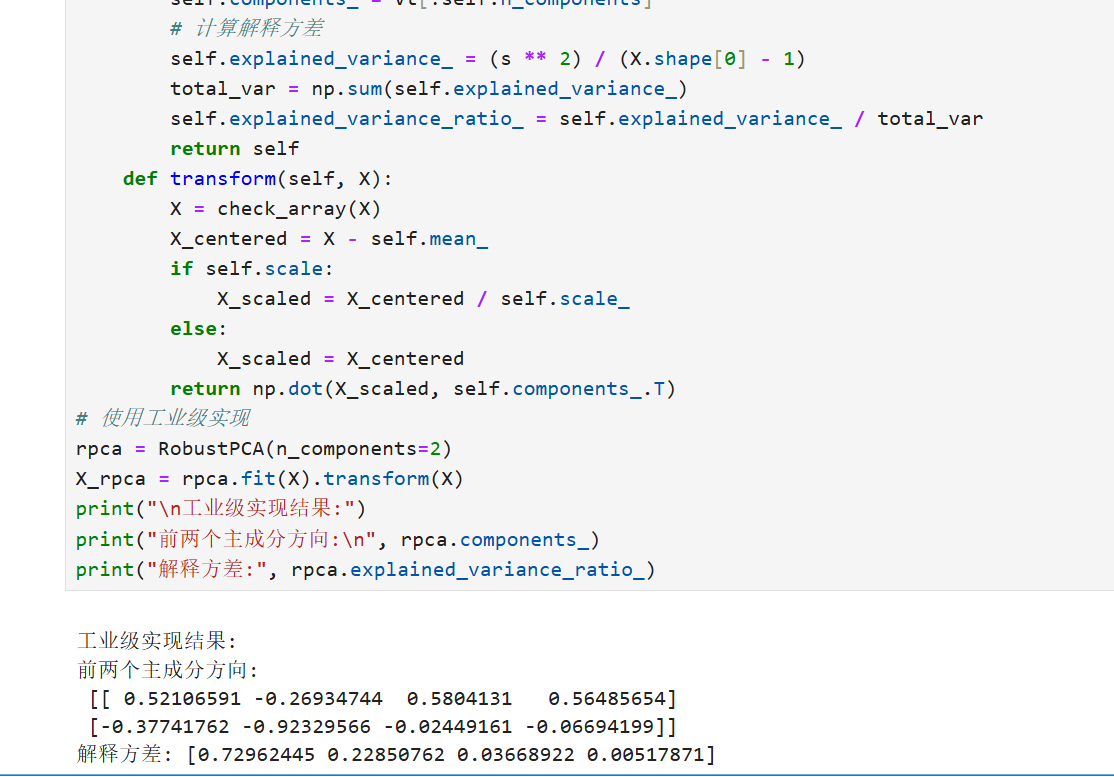
4.异常检测方法
4.1基本概念
异常检测(Anomaly Detection)是识别数据中不符合预期模式或行为的观测值的过程,在金融欺诈检测、工业设备故障预测、网络安全等领域有广泛应用。
异常类型分类
点异常:单个数据点异常(如信用卡欺诈)
上下文异常:特定上下文中异常(如夏季低温)
集体异常:相关数据集合异常(如网络DDoS攻击)
核心挑战
异常样本稀少且形式多样
正常行为边界模糊
数据分布动态变化
标签获取成本高昂
4.2代码介绍
基于统计的异常检测方法(Statistical-Based)
方法介绍:
统计方法基于数据的分布特性,识别那些明显偏离分布的值。常见的方式如:均值-标准差法、箱型图法(IQR)等。适用于数值型数据,当数据满足或接近正态分布时效果最佳。
均值-标准差法
我们认为距离均值超过3倍标准差的点为异常值。
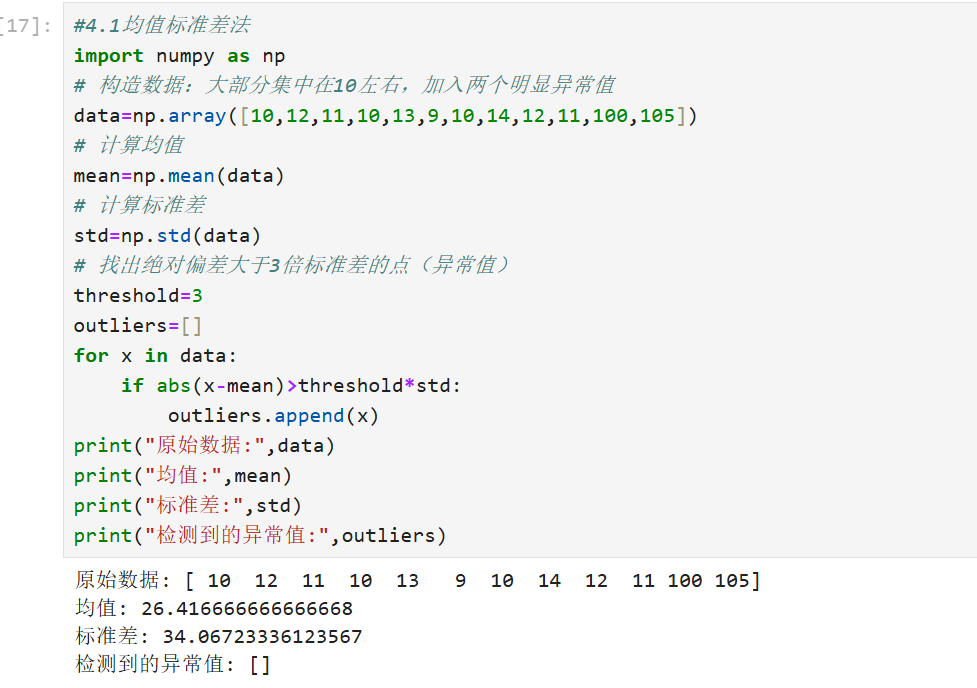
基于距离的异常检测方法(Distance-Based)
方法介绍:
基于距离的方法认为:远离其他数据点的数据是异常的。典型方法如:KNN距离法(k-近邻)。适合中等规模数据。
K近邻平均距离法(简单2维可视化)

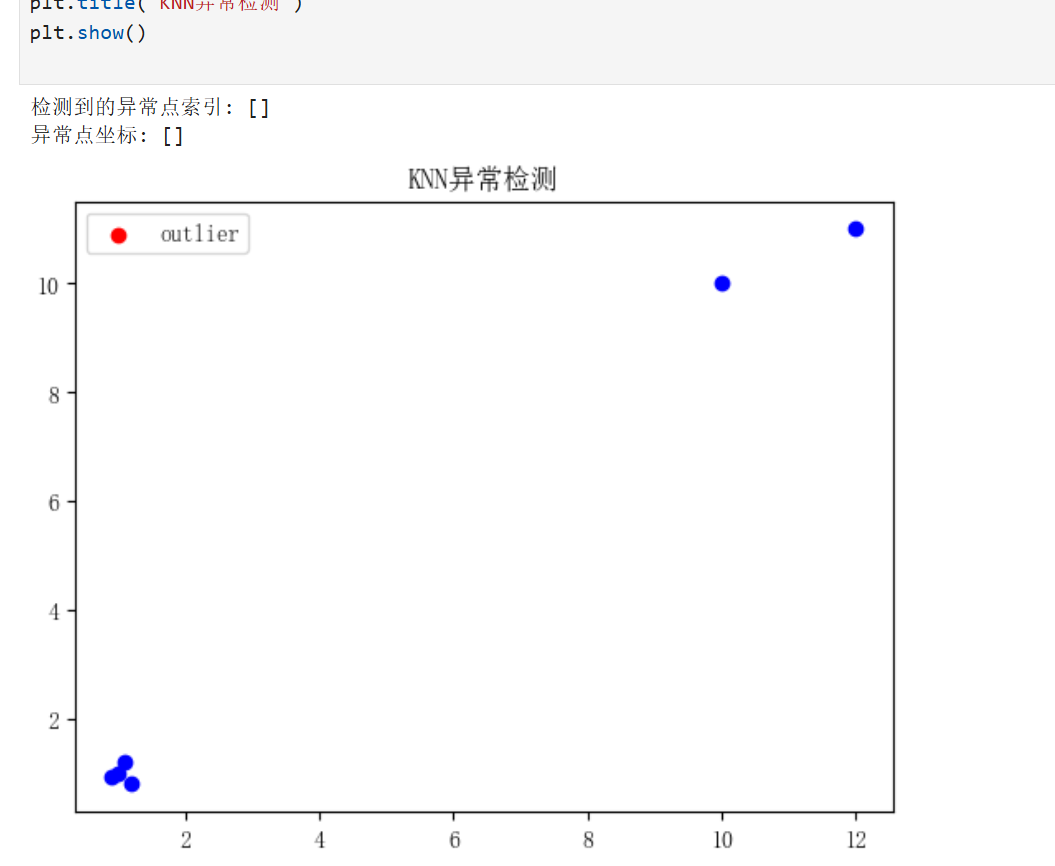
基于机器学习模型的异常检测(如Isolation Forest)
方法介绍:
Isolation Forest 是一种专门为异常检测设计的算法,适用于大规模数据。它通过随机分裂特征,将异常值更容易孤立。
Isolation Forest

五、模型评估与验证
1.训练集/测试集划分
1.1基础概念
划分目的
模型训练:训练集用于构建模型参数
泛化评估:测试集评估模型在未知数据上的表现
过拟合检测:识别模型是否过度记忆训练数据
超参数调优:验证集用于调整模型参数
完整数据集
├── 训练集 (60-80%) → 模型学习
│ └── 子集:验证集 (10-20%训练集) → 参数调优
└── 测试集 (20-40%) → 最终评估
关键比例考虑因素
| 因素 | 推荐比例 | 说明 |
|---|---|---|
| 数据集大小 | 小数据集(70/30) 大数据集(90/10) | 小数据集需更多测试样本 |
| 数据维度 | 高维数据增加训练比例 | 避免维度灾难 |
| 类别平衡 | 分层抽样保持比例 | 尤其分类问题 |
| 时间序列 | 严格按时间顺序 | 未来不能预测过去 |
数据集大小
小数据集推荐采用70%训练集和30%测试集的比例划分,确保测试集有足够样本评估模型性能。大数据集可采用90%训练集和10%测试集,因数据量充足时测试集比例可适当降低。
数据维度
高维数据需增加训练集比例,防止测试集样本过少导致维度灾难。通常特征维度越高,训练集比例需相应提高,以确保模型能充分学习特征关系。
类别平衡
分类问题中需通过分层抽样保持训练集和测试集的类别比例一致。避免因随机划分导致某些类别在测试集中样本过少,影响评估的准确性。
时间序列
时间序列数据必须严格按时间顺序划分,训练集时间早于测试集。任何未来时间点的数据都不能出现在训练集中,以避免数据泄露。
1.2基本代码实现(示例)
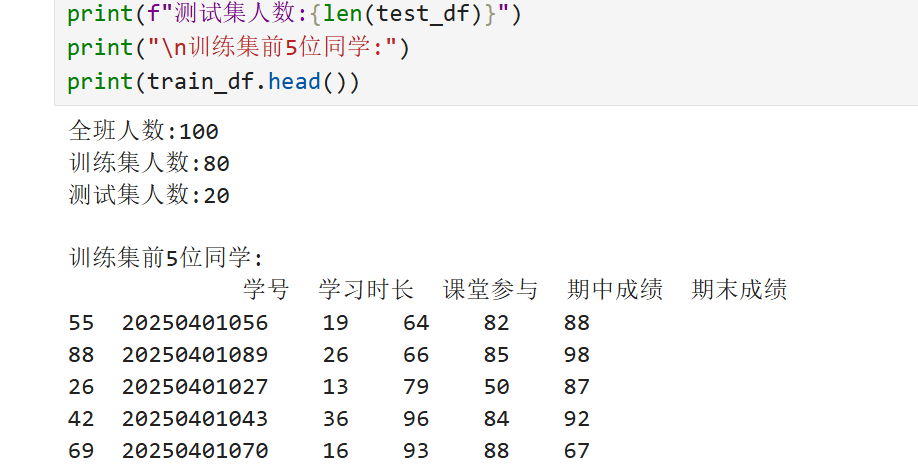


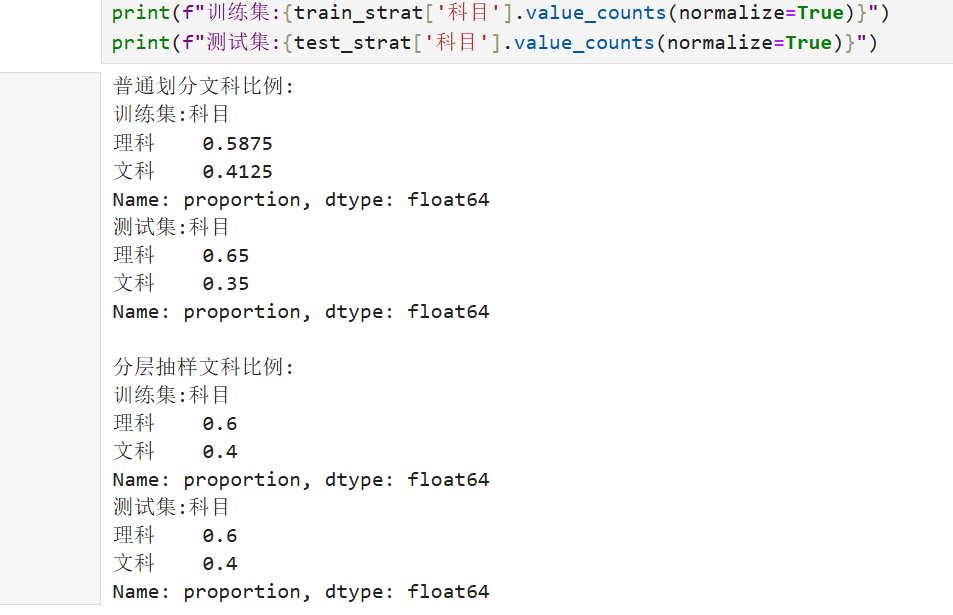
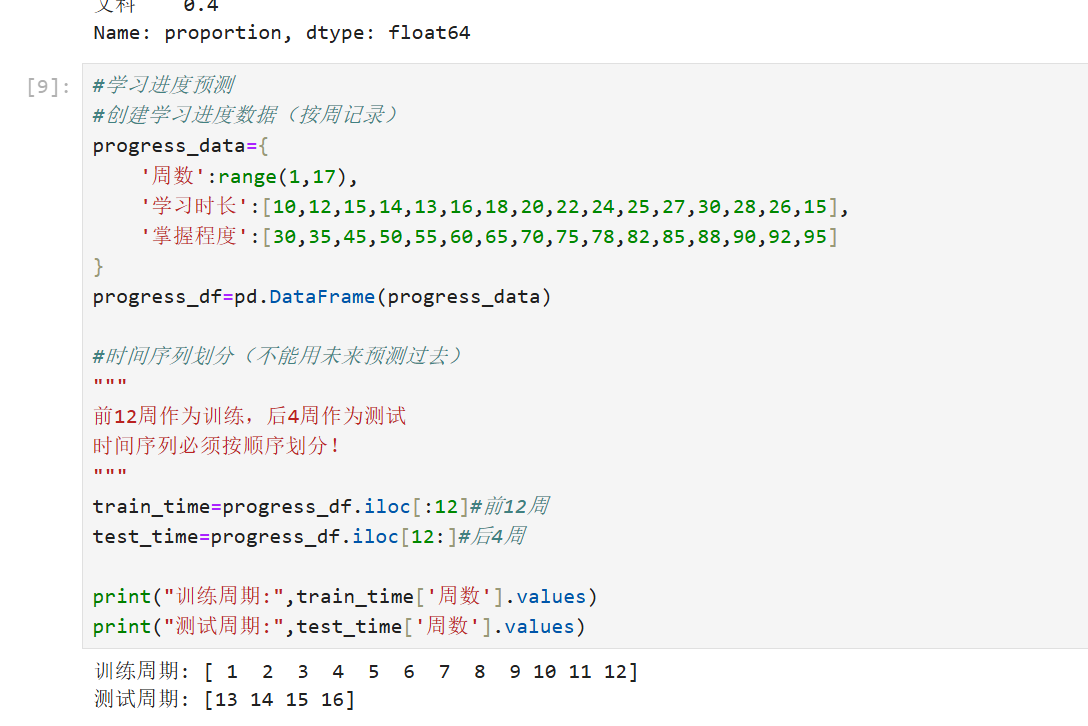
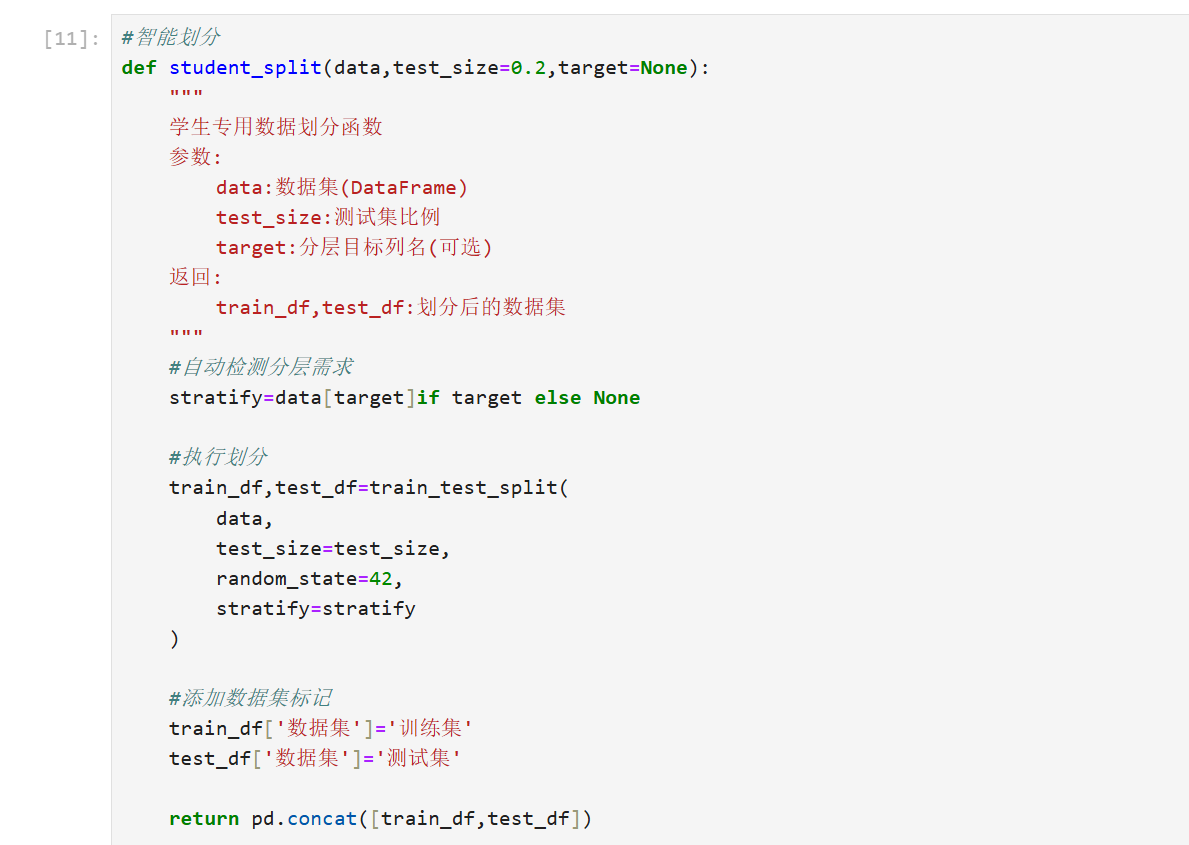
智能划分

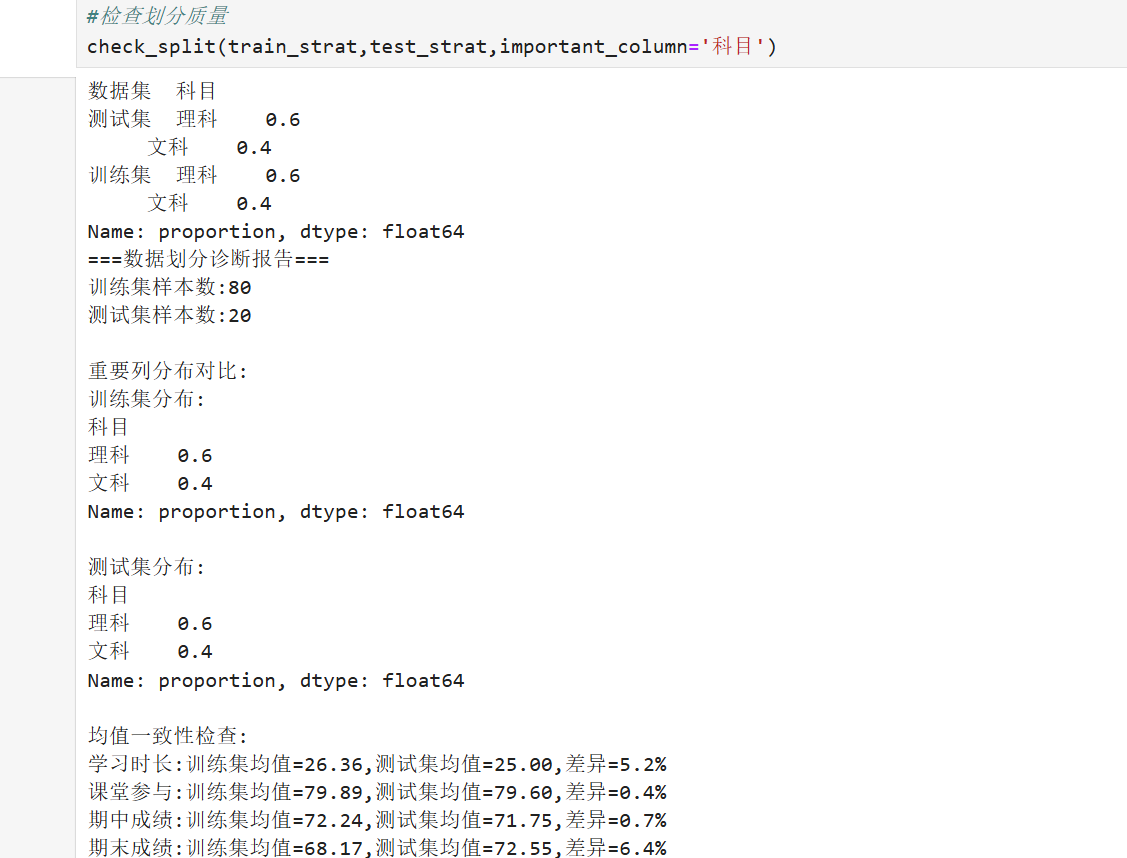
2.交叉验证技术
交叉验证是一种用于评估机器学习模型泛化能力的技术,通过将数据集划分为多个子集来避免过拟合和欠拟合。核心思想是重复训练和验证过程,以获取更可靠的性能估计。常见类型包括:
- k折交叉验证(k-fold Cross Validation):将数据集随机分为k个大小相似的子集(称为“折”)。每次迭代使用其中一个折作为验证集,其余k-1个作为训练集。过程重复k次,每次选择不同的验证集。最终性能指标是所有迭代的平均值。
公式表示平均误差:
平均误差
其中是第i次迭代的误差(如分类错误率或回归均方误差),
是折数(通常取5或10)。
- 留一交叉验证(Leave-One-Out Cross Validation, LOOCV):k折交叉验证的特例,k等于样本数n。每次只留出一个样本作为验证集,其余作为训练集。重复n次。优点是充分利用数据,但计算成本高。
- 分层k折交叉验证(Stratified k-fold):用于分类问题,确保每个折中类别比例与原始数据集一致,避免偏差。
优点:减少随机划分带来的方差,提供更稳健的模型评估。缺点:计算开销大,尤其在大数据集上。应用场景:模型选择、超参数调优和避免数据泄露。
交叉验证是机器学习中用于评估模型性能的关键技术,它通过将数据集分割成多个子集,反复训练和测试模型来减少过拟合风险。主要函数通常出现在编程库(如Python的scikit-learn)中,用于实现不同交叉验证策略。
1. KFold函数
- 用途:实现K折交叉验证,将数据集分成K个等份子集(folds),每次用K-1份训练,1份测试,重复K次。
- 关键参数:
n_splits:指定K值(默认5),例如K=5表示5折交叉验证。shuffle:是否随机打乱数据(默认为False)。random_state:随机种子,确保可重复性。
- 代码示例(Python,使用scikit-learn):
from sklearn.model_selection import KFold import numpy as np # 创建示例数据集 X = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]]) y = np.array([1, 2, 3, 4, 5]) # 初始化KFold对象 kf = KFold(n_splits=3, shuffle=True, random_state=42) # 遍历每个折叠进行训练和测试 for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] print(f"训练索引: {train_index}, 测试索引: {test_index}")- 输出示例:每次迭代打印训练和测试索引,例如第一折训练索引[0,2,3],测试索引[1,4]。
2. cross_val_score函数
- 用途:计算模型在交叉验证中的平均性能分数(如准确率或均方误差),简化评估过程。
- 关键参数:
estimator:模型对象(如分类器或回归器)。X:特征数据。y:标签数据。cv:交叉验证策略(如KFold对象或整数K)。scoring:评估指标(如'accuracy'或'r2')。
- 数学基础:平均分数公式为
,其中
是第i折的指标值。
- 代码示例(Python,使用scikit-learn):
from sklearn.model_selection import cross_val_score from sklearn.ensemble import RandomForestClassifier # 创建模型和数据 model = RandomForestClassifier(random_state=42) X, y = ... # 假设已加载数据(如Iris数据集) # 计算5折交叉验证的准确率平均分 scores = cross_val_score(model, X, y, cv=5, scoring='accuracy') print(f"各折分数: {scores}") print(f"平均准确率: {scores.mean():.2f}")- 输出示例:各折分数[0.95, 0.92, 0.93, 0.94, 0.91],平均准确率0.93。
3. StratifiedKFold函数
- 用途:分层K折交叉验证,确保每个折叠中类别的比例与原始数据集一致,适用于不平衡数据。
- 关键参数:
n_splits:K值(默认5)。shuffle:是否随机打乱。random_state:随机种子。
- 代码示例(Python,使用scikit-learn):
from sklearn.model_selection import StratifiedKFold # 初始化StratifiedKFold对象 skf = StratifiedKFold(n_splits=3, shuffle=True, random_state=42) # 遍历折叠(假设y有类别标签) for train_index, test_index in skf.split(X, y): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] print(f"训练类别分布: {np.bincount(y_train)}, 测试类别分布: {np.bincount(y_test)}")- 输出示例:每个折叠的类别分布保持平衡,例如训练集类别比例[40%, 30%, 30%],测试集比例相同。
4. LeaveOneOut函数
- 用途:留一法交叉验证,每次只留一个样本作为测试集,其余全部训练。适用于小数据集,但计算开销大。
- 关键参数:无主要参数,直接创建对象。
- 数学基础:测试次数等于样本数$N$,性能平均为 $$\frac{1}{N} \sum_{i=1}^{N} \text{metric}_i$$。
- 代码示例(Python,使用scikit-learn):
from sklearn.model_selection import LeaveOneOut # 初始化LeaveOneOut对象 loo = LeaveOneOut() # 遍历每个样本 for train_index, test_index in loo.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] # 训练模型并计算分数(此处省略模型代码) print(f"测试样本索引: {test_index}")- 输出示例:每次迭代测试一个样本,如索引0, 1, ..., N-1。
总结
- 主要函数比较:
KFold:通用K折验证,适用于大多数场景。cross_val_score:高效计算模型平均性能。StratifiedKFold:处理不平衡数据。LeaveOneOut:高精度但计算密集。
- 使用建议:选择函数时考虑数据集大小和平衡性;K值通常设为5或10。实践中,结合
cross_val_score能快速评估模型。 - 注意事项:确保数据预处理(如标准化)在交叉验证循环内进行,避免数据泄露。所有函数均需导入
sklearn.model_selection模块。
3.分类评估指标
分类评估指标用于衡量分类模型(如二分类或多分类)的性能,基于预测结果与实际标签的比较。关键指标包括:
- 准确率(Accuracy):正确预测的样本占总样本的比例。
准确率
其中TP(True Positive)是真正例,TN(True Negative)是真负例,FP(False Positive)是假正例,FN(False Negative)是假负例。简单但易受类别不平衡影响。 - 精确率(Precision):预测为正例的样本中,实际为正例的比例,关注预测的“准度”。
精确率 - 召回率(Recall):实际为正例的样本中,被正确预测的比例,关注模型的“查全率”。
召回率 - F1分数(F1 Score):精确率和召回率的调和平均,用于平衡两者。尤其适用于类别不平衡数据。
- AUC-ROC曲线(Area Under the ROC Curve):ROC曲线以假正率(FPR)为横轴、召回率为纵轴,AUC值表示模型区分正负类的能力。AUC接近1表示性能好。
其他指标:如特异度(Specificity),用于医疗诊断等场景。选择指标需根据问题:例如,欺诈检测重视召回率,垃圾邮件过滤重视精确率。
使用scikit-learn库计算这些指标(假设已有真实标签和预测标签):
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
def evaluate_classification(y_true, y_pred):
# 计算混淆矩阵相关值(实际中可使用sklearn的confusion_matrix)
# 计算主要指标
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)
auc = roc_auc_score(y_true, y_pred) # 假设y_pred是概率值
# 返回结果字典
return {
"Accuracy": accuracy,
"Precision": precision,
"Recall": recall,
"F1-Score": f1,
"AUC": auc
}
# 示例用法
# y_true = [0, 1, 1, 0, 1] # 真实标签
# y_pred = [0, 1, 0, 0, 1] # 预测标签
# print(evaluate_classification(y_true, y_pred))
总结
这些指标各有侧重:准确率提供整体视图,精确率和召回率关注特定类别,F1分数平衡两者,ROC/AUC评估阈值鲁棒性。在实际应用中,应根据问题需求选择合适指标(如医疗领域优先召回率,金融领域优先精确率)。结合混淆矩阵分析,能更全面地评估模型性能。
4.回归评估指标
回归评估指标用于回归模型(如预测连续值),衡量预测值与实际值之间的差异。常见指标包括:
- 均方误差(Mean Squared Error, MSE):预测值与实际值差的平方的平均值,对异常值敏感。
其中是实际值,
是预测值,
是样本数。
- 均方根误差(Root Mean Squared Error, RMSE):MSE的平方根,单位与实际值一致,更易解释。
- 平均绝对误差(Mean Absolute Error, MAE):预测值与实际值绝对差的平均值,对异常值鲁棒。
- 决定系数(R-squared, R²):表示模型解释数据变异性的比例,范围在0到1之间。接近1表示模型拟合好。
其中是实际值的均值。
优点:MSE和RMSE强调大误差,MAE更稳健。R²提供相对性能。应用场景:房价预测、销量预测等连续值问题。
在Python中,回归模型的评估主要通过scikit-learn库实现,以下是核心评估函数及使用说明:
1. 均方误差 (MSE)
函数:sklearn.metrics.mean_squared_error(y_true, y_pred)
特点:
- 对异常值敏感(平方放大误差)
- 值域 $[0, +\infty)$,越小越好
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred)
2. 均方根误差 (RMSE)
计算方式:MSE的平方根
特点:
- 与目标变量单位一致,更易解释
rmse = mean_squared_error(y_true, y_pred, squared=False)
3. 平均绝对误差 (MAE)
函数:sklearn.metrics.mean_absolute_error(y_true, y_pred)
特点:
- 鲁棒性强(不受异常值过度影响)
- 值域
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_true, y_pred)
4. 决定系数 ( )
)
函数:sklearn.metrics.r2_score(y_true, y_pred)
特点:
- 值域
,越接近1越好
- 表示模型解释的方差比例
from sklearn.metrics import r2_score
r2 = r2_score(y_true, y_pred)
5. 修正 (Adjusted
(Adjusted  )
)
公式:
其中 $n$ 是样本数,$p$ 是特征数
特点:
- 惩罚多余特征,防止过拟合
- scikit-learn无直接函数,需手动计算:
n = len(y_true)
p = X.shape[1] # 特征数量
adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
综合使用示例
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
print(f"MSE: {mean_squared_error(y_true, y_pred):.2f}")
print(f"RMSE: {mean_squared_error(y_true, y_pred, squared=False):.2f}")
print(f"MAE: {mean_absolute_error(y_true, y_pred):.2f}")
print(f"R²: {r2_score(y_true, y_pred):.2f}")
选择建议:
- 关注异常值影响时用 MAE
- 需要与目标变量同单位度量时用 RMSE
- 评估模型整体解释能力用
- 比较不同特征数量的模型用 Adjusted
5.混淆矩阵与分类报告
混淆矩阵是分类模型评估的核心工具,以表格形式展示预测结果与实际标签的对比;分类报告则基于混淆矩阵生成汇总指标报告。两者结合提供全面性能分析。
- 混淆矩阵(Confusion Matrix):一个$n \times n$矩阵($n$为类别数),行表示实际类别,列表示预测类别。
例如,二分类混淆矩阵:实际 \ 预测 正例 负例 正例 TP FN 负例 FP TN 从中可计算所有分类指标(如准确率、精确率)。多分类时,矩阵扩展为多行多列。 - 分类报告(Classification Report):基于混淆矩阵生成的总结性报告,通常包括每个类别的精确率、召回率、F1分数,以及宏观平均(macro-average)或加权平均(weighted-average)。
例如,在Python的scikit-learn库中,classification_report函数输出:- 每个类别的指标:精确率、召回率、F1分数、支持数(样本数)。
- 总体平均:如宏平均F1
($n$为类别数),加权平均F1
(
为类别权重)。
优点:直观展示错误类型(如FN表示漏报),帮助识别模型弱点(如特定类别性能差)。应用场景:模型调试、性能报告和比较。
在机器学习分类任务中,混淆矩阵(Confusion Matrix)和分类报告(Classification Report)是评估模型性能的核心工具。Python的scikit-learn库提供了简洁的实现函数。
1. 混淆矩阵函数:confusion_matrix
功能:生成N×N矩阵(N为类别数),直观展示分类结果。
结构:
- 行:真实类别
- 列:预测类别
- 对角线:正确预测样本数
关键指标:
- TP(True Positive):正确预测的正例
- FP(False Positive):负例误判为正例
- FN(False Negative):正例误判为负例
- TN(True Negative):正确预测的负例
语法:
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_true, y_pred)
示例(二分类):
# 真实标签:[0,1,0,1], 预测标签:[0,1,1,0]
cm = confusion_matrix([0,1,0,1], [0,1,1,0])
# 输出:
# [[1 1] # 真实0类:正确预测1个,错误预测1个
# [1 1]] # 真实1类:正确预测1个,错误预测1个
2. 分类报告函数:classification_report
功能:生成包含多维度指标的文本报告,支持多分类任务。
核心指标(每类单独计算):
- 精确率(Precision):
(预测为正例的样本中实际为正的比例) - 召回率(Recall):
(实际正例中被正确预测的比例) - F1分数:
(精确率和召回率的调和平均) - 支持数(Support):该类别的样本总数
语法:
from sklearn.metrics import classification_report
report = classification_report(y_true, y_pred)
示例输出:
precision recall f1-score support
0 0.67 0.67 0.67 3
1 0.50 0.50 0.50 2
accuracy 0.60 5
macro avg 0.58 0.58 0.58 5
weighted avg 0.60 0.60 0.60 5
六、特征工程进阶
1.多项式特征生成
1.1基本概况
多项式特征生成是特征工程的核心技术,通过创建原始特征的高阶组合(如平方、立方及交叉项),将线性模型扩展为非线性模型。其核心思想是将特征空间映射到更高维度,从而捕捉特征间的复杂交互关系。
数学原理
设原始特征向量为 ,多项式转换函数定义为:
其中 为多项式阶数。例如当
时:
核心作用
-
非线性关系建模
线性模型扩展为:
可拟合抛物线等复杂模式
-
特征交互捕获
交叉项显式建模特征间的协同效应
-
维度扩展
原始n维特征经 $d$ 阶扩展后维度为:例如
→ 66维特征空间
1.2代码示例

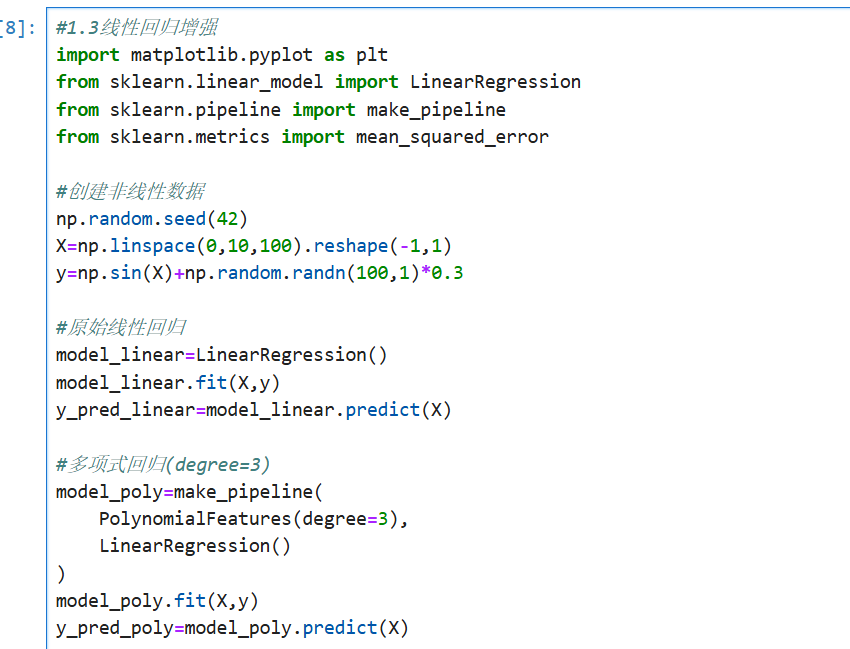
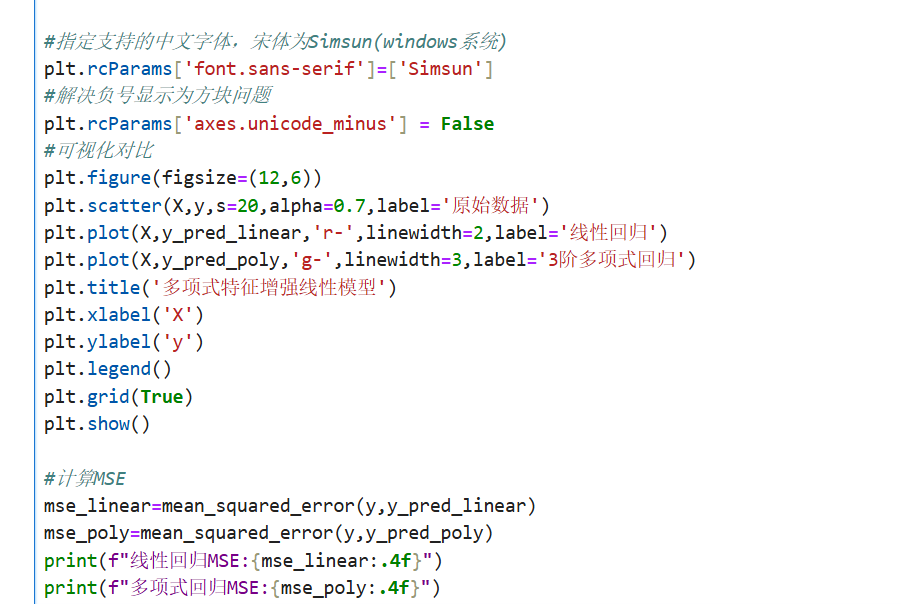
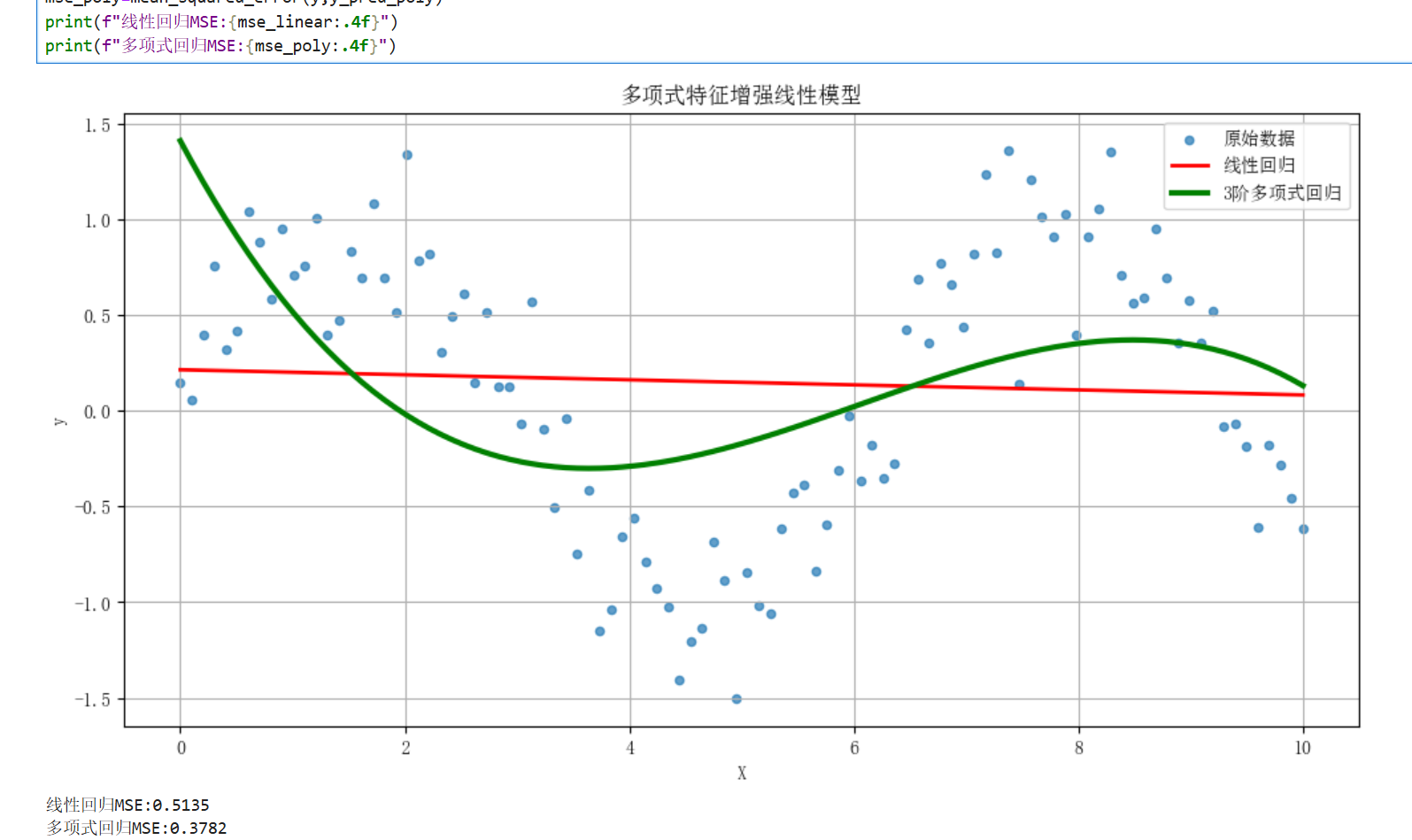
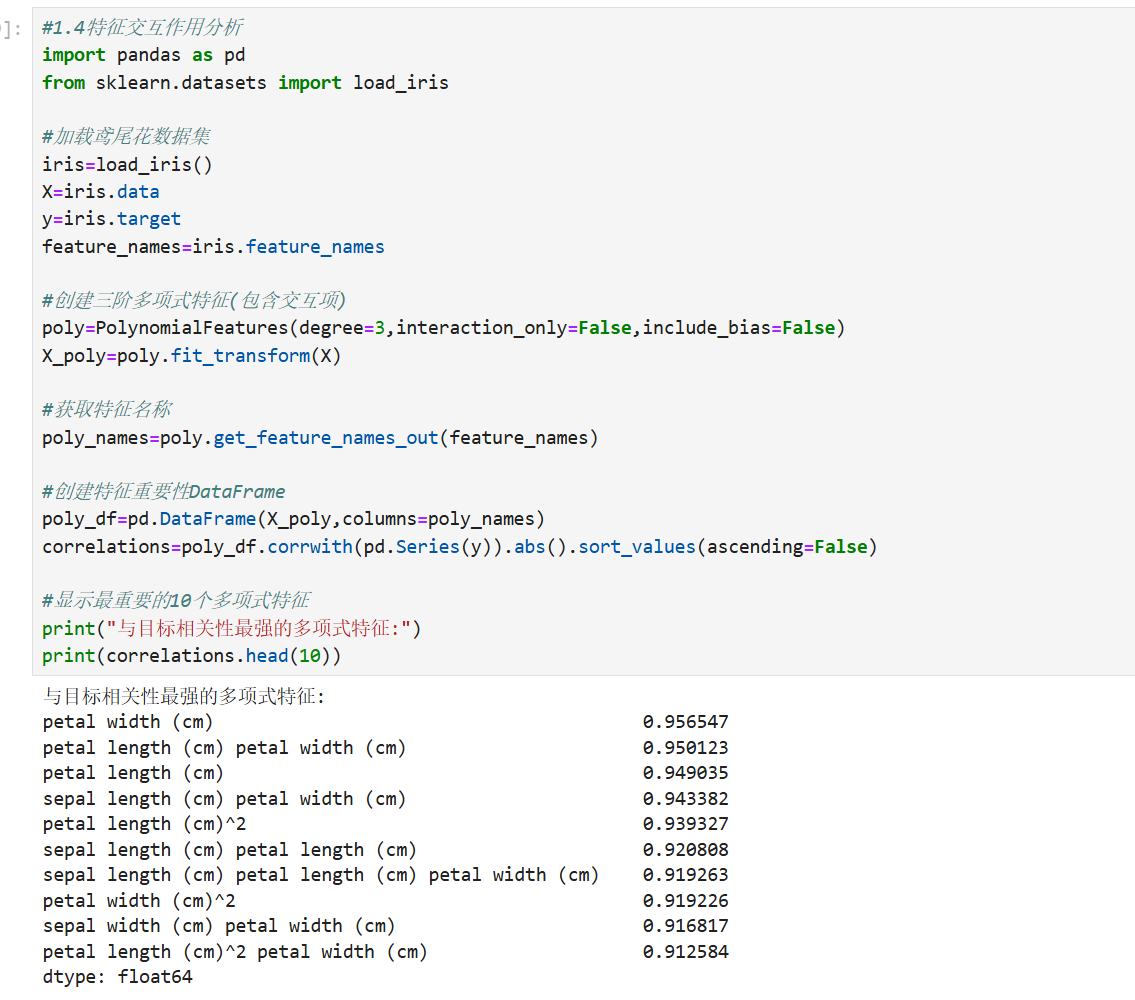
2.自定义转换器
2.1基本概念
在数据处理和机器学习中,自定义转换器(Custom Transformer)是一种强大的工具,允许用户创建符合特定需求的数据预处理步骤。它通过封装转换逻辑,实现与scikit-learn等库的无缝集成,提升代码复用性和可维护性。
核心概念
-
转换器接口
自定义转换器需实现三个核心方法:fit():学习数据特征(如统计量)transform():应用转换逻辑fit_transform():组合前两步(可选)
-
scikit-learn集成
通过继承BaseEstimator和TransformerMixin基类,可自动获得:- 参数校验
- Pipeline兼容性
- 超参数调优支持
创建步骤
from sklearn.base import BaseEstimator, TransformerMixin
import numpy as np
class LogTransformer(BaseEstimator, TransformerMixin):
def __init__(self, add_constant=1):
self.add_constant = add_constant # 防止对0取对数
def fit(self, X, y=None):
return self # 无状态转换器不需学习
def transform(self, X):
# 对数值特征取对数
return np.log(X + self.add_constant)
关键特性
-
参数传递
通过__init__初始化参数,支持网格搜索:param_grid = {'add_constant': [1, 0.5]} GridSearchCV(LogTransformer(), param_grid) -
Pipeline集成
与标准转换器协同工作:pipeline = Pipeline([ ('scaler', StandardScaler()), ('log', LogTransformer()), ('svm', SVC()) ]) -
类型处理
可设计条件逻辑处理混合数据类型:def transform(self, X): if X.dtype == np.object_: return self._handle_categorical(X) else: return self._handle_numeric(X)
应用场景
-
特征工程
- 创建交互特征:$x_1 \times x_2$
- 分箱离散化:$x \mapsto \text{bin}(x)$
-
数据清洗
- 自定义缺失值填充
- 异常值修正
-
领域适配
- 医学图像的特殊归一化
- 金融数据的波动率转换
最佳实践
- 幂等性:确保多次转换结果一致
- 可逆性:必要时实现
inverse_transform() - 内存优化:大数据集使用增量
partial_fit()
2.2代码实现
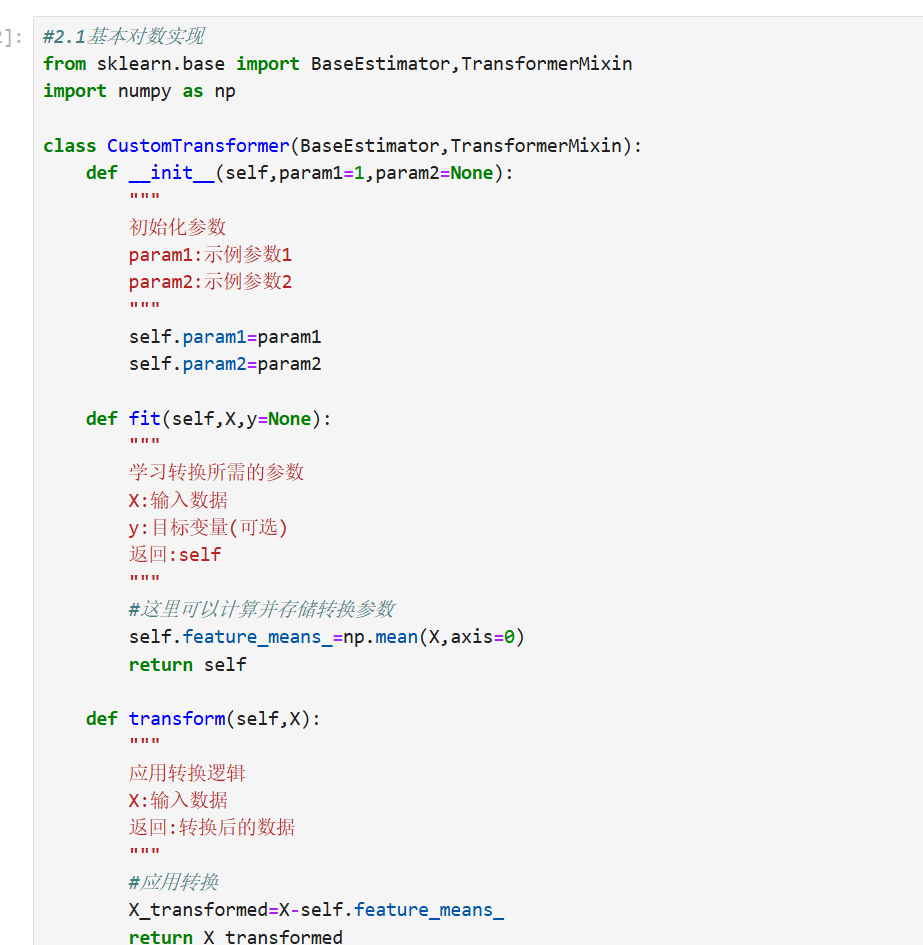
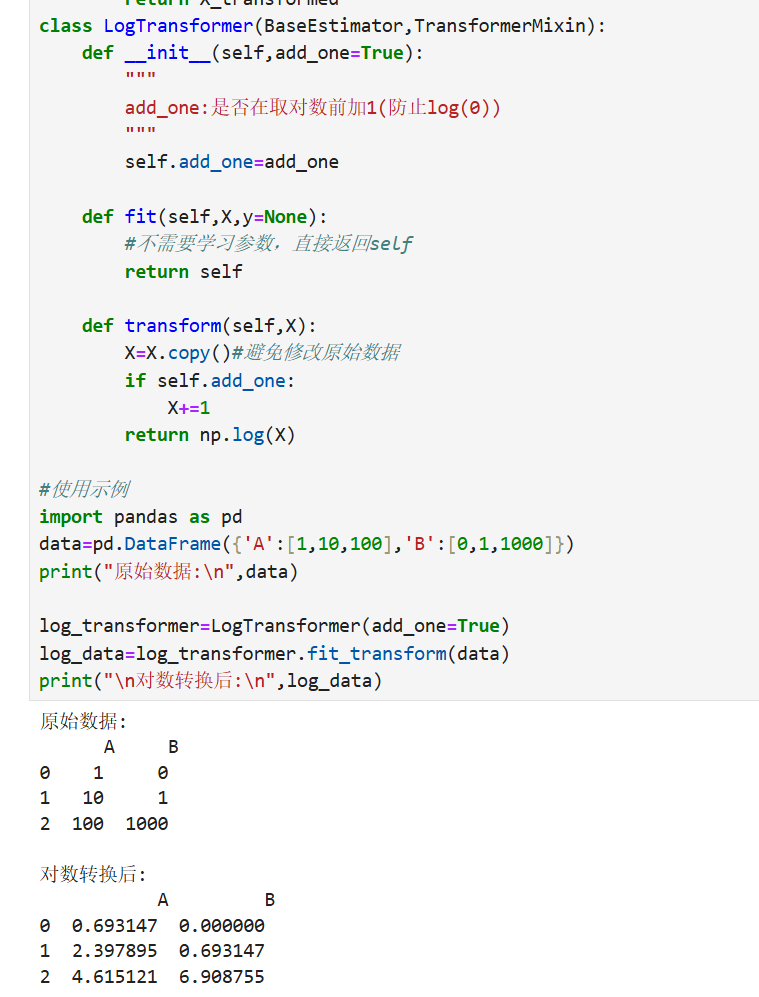

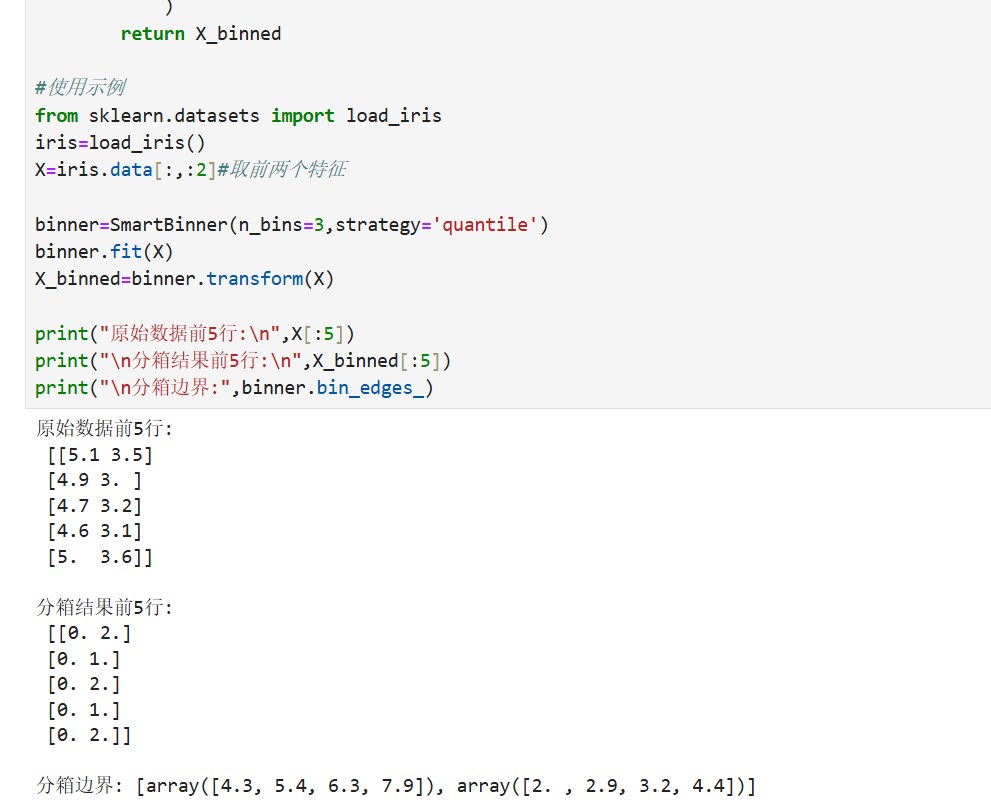
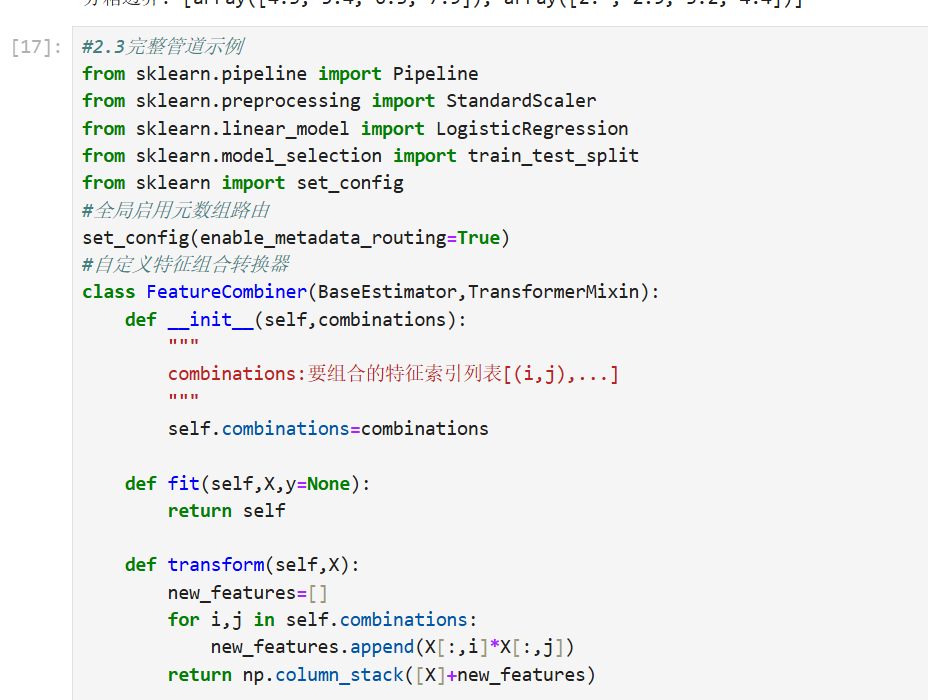



3.文本特征提取
文本特征提取是自然语言处理(NLP)中的关键步骤,旨在将非结构化的文本数据转换为数值特征向量,以便机器学习模型能够处理。它帮助捕捉文本中的语义、语法和统计信息,广泛应用于文本分类、情感分析、信息检索等领域。下面,我将逐步介绍主要方法,确保解释清晰且实用。
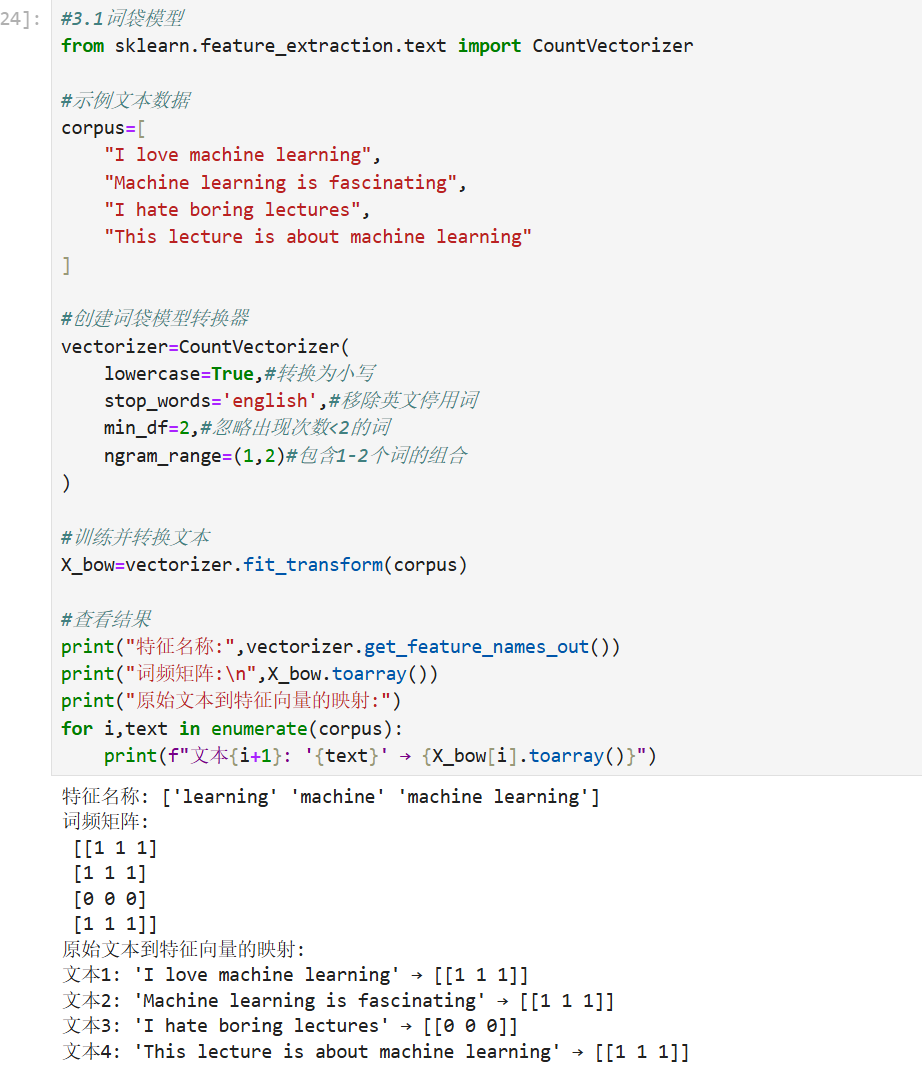
1. 词袋模型(Bag of Words, BoW)
- 原理:将文本视为单词的集合,忽略顺序和语法,只统计每个单词的出现频率。
- 数学表示:对于一个文档集合,每个文档被表示为一个向量,其中每个维度对应一个单词的频率。
- 例如,文档
的向量:
,其中
是单词
的频率。
- 例如,文档
- 优点:简单高效,易于实现。
- 缺点:忽略单词顺序和上下文,可能导致信息丢失。
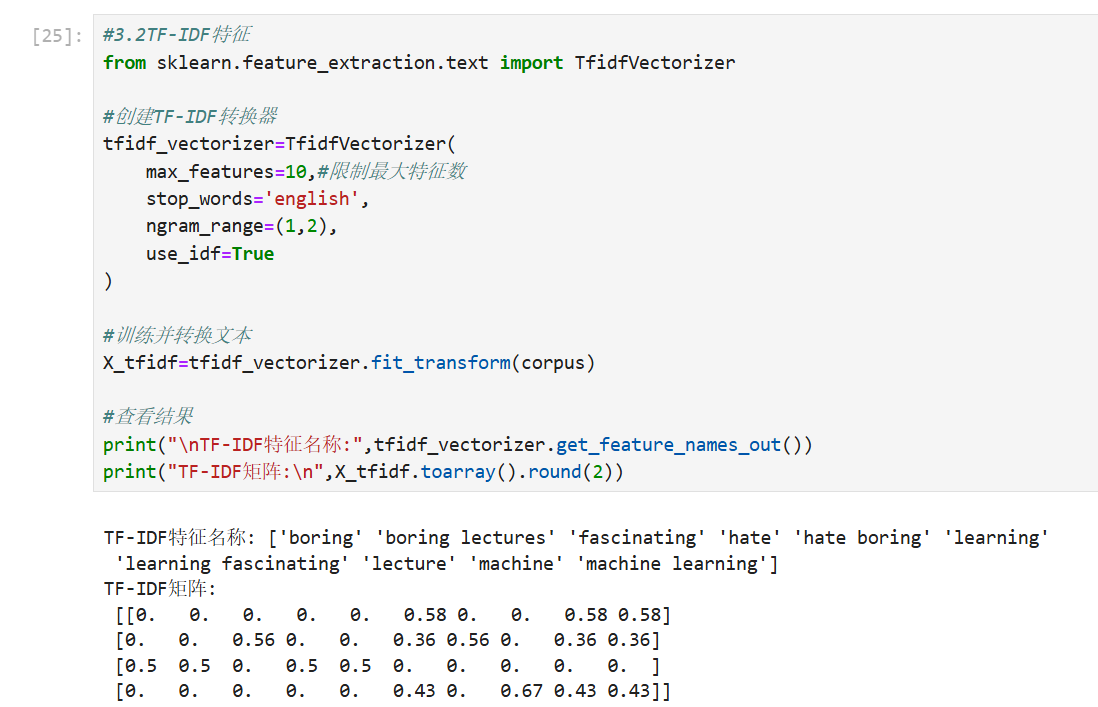
2. TF-IDF(Term Frequency-Inverse Document Frequency)
- 原理:衡量单词在文档中的重要性,结合词频(TF)和逆文档频率(IDF)。TF 表示单词在文档中的常见程度,IDF 降低常见单词的权重。
- 公式:
- 词频(TF):
,其中
是单词
在文档
中的出现次数。
- 逆文档频率(IDF):
,其中
是文档总数,
是包含单词 $t$ 的文档数。
- TF-IDF 值:
- 词频(TF):
- 优点:能突出重要单词,减少常见词的影响。
- 缺点:仍忽略单词顺序。
3. n-grams
- 原理:考虑连续单词序列(如二元组、三元组),捕捉局部上下文。
- 例如,二元组(bigram)将 "good movie" 视为一个特征。
- 数学表示:文档向量包含 n-gram 的频率,例如,对于 bigram:
。
- 优点:保留部分顺序信息,提升模型表现。
- 缺点:特征维度可能爆炸,增加计算成本。


4. 词嵌入(Word Embeddings)
- 原理:将单词映射到低维连续向量空间,捕捉语义相似性。常用方法包括 Word2Vec 和 GloVe。
- Word2Vec:基于神经网络,预测上下文单词。
- GloVe:基于全局词共现矩阵。
- 数学表示:每个单词
表示为向量
,其中
是嵌入维度(如 100 或 300)。
- 优点:能处理语义关系(如 "king" - "man" + "woman" ≈ "queen")。
- 缺点:需要大量训练数据,计算开销大。




5. 其他方法
- 主题模型(如 LDA):将文档表示为潜在主题的分布。
- 深度学习特征:使用预训练模型(如 BERT)直接提取上下文感知特征。
文本特征提取是文本分析的基础,选择合适的方法取决于任务需求:BoW 适合简单快速应用,TF-IDF 提升重要性权重,n-grams 捕捉序列,词嵌入处理语义。实际应用中,常结合多种方法,并通过交叉验证优化。确保特征提取后,进行标准化或降维(如 PCA)以提高模型性能。
BERT 上下文嵌入

4.时间序列特征处理
4.1时间序列特征处理概述
时间序列特征处理是将原始时间序列数据转换为有意义的特征,以便用于机器学习模型训练。Scikit-learn 提供了多种工具和方法来处理时间序列数据,尽管它本身不是一个专门的时间序列库,但可以结合其他库(如 pandas、statsmodels)实现高效的特征提取。
时间序列特征提取方法
滑动窗口统计特征
通过滑动窗口计算统计量(均值、方差、最大值、最小值等)作为特征。例如,使用 pandas 的 rolling 方法提取窗口统计量:
import pandas as pd
# 示例时间序列数据
data = pd.Series([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# 计算滑动窗口均值和标准差
window_size = 3
rolling_mean = data.rolling(window=window_size).mean()
rolling_std = data.rolling(window=window_size).std()
滞后特征(Lag Features)
将时间序列的过去值作为特征引入当前时间点。例如,使用 pandas 的 shift 方法:
# 创建滞后特征
lag_1 = data.shift(1) # 滞后1期
lag_2 = data.shift(2) # 滞后2期
差分与季节性差分
用于消除时间序列的趋势和季节性。一阶差分和季节性差分的实现:
# 一阶差分
diff_1 = data.diff(1)
# 季节性差分(假设周期为4)
seasonal_diff = data.diff(4)
Scikit-learn 中的特征处理工具:
多项式特征扩展
PolynomialFeatures 可以生成时间序列的非线性特征:
from sklearn.preprocessing import PolynomialFeatures
# 假设时间戳作为特征
timestamps = [[1], [2], [3], [4]]
poly = PolynomialFeatures(degree=2)
poly_features = poly.fit_transform(timestamps)
标准化与归一化
使用 StandardScaler 或 MinMaxScaler 对时间序列特征进行标准化:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data.values.reshape(-1, 1))
时间序列分解
结合 statsmodels 进行趋势和季节性分解:
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(data, model='additive', period=1)
trend = result.trend
seasonal = result.seasonal
residual = result.resid
时间序列特征选择:
基于模型的特征选择
使用 SelectFromModel 结合回归模型(如 Lasso)选择重要特征:
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import Lasso
# 假设 X 是特征矩阵,y 是目标变量
selector = SelectFromModel(Lasso(alpha=0.1))
selected_features = selector.fit_transform(X, y)
递归特征消除(RFE)
通过递归方式剔除不重要的特征:
from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
rfe = RFE(estimator=LinearRegression(), n_features_to_select=5)
rfe.fit(X, y)
selected_features = X.columns[rfe.support_]
时间序列特征工程与流水线:
结合 Pipeline 将特征处理步骤串联:
from sklearn.pipeline import Pipeline
from sklearn.linear_model import Ridge
pipeline = Pipeline([
('scaler', StandardScaler()),
('feature_selection', SelectFromModel(Lasso())),
('regressor', Ridge())
])
pipeline.fit(X_train, y_train)
通过上述方法,可以高效地完成时间序列特征处理,并将其应用于机器学习模型。
4.2完整代码实现



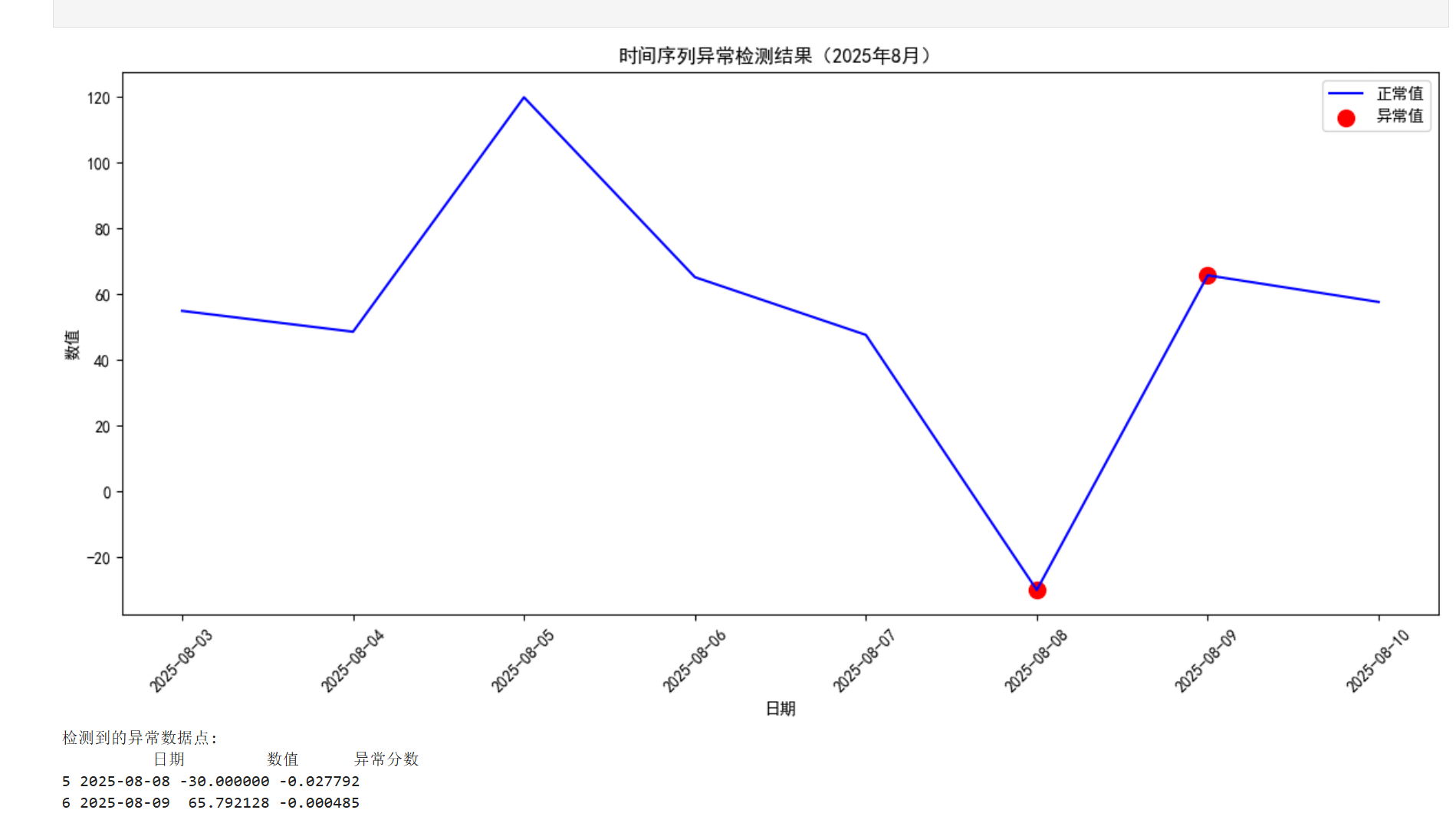
七、模型优化
-
学习曲线分析
-
特征重要性评估
-
模型持久化
1.超参数调优(网格搜索、随机搜索)
1. 网格搜索 (GridSearchCV)
通过遍历预定义参数组合寻找最优解,适用于参数空间较小的情况。
通过穷举指定的参数组合进行交叉验证,寻找最优超参数。主要参数:
estimator: 基础模型(如RandomForestClassifier())
param_grid: 参数网格(字典格式,如{'n_estimators': [50, 100]})
cv: 交叉验证折数
scoring: 评估指标(如'accuracy')
调用.fit(X_train, y_train)后,通过.best_params_获取最优参数。
核心函数:
from sklearn.model_selection import GridSearchCV
param_grid = {
'n_estimators': [50, 100, 200], # 决策树数量
'max_depth': [3, 5, None] # 树的最大深度
}
gs = GridSearchCV(
estimator=RandomForestClassifier(), # 基础模型
param_grid=param_grid, # 参数网格
cv=5, # 交叉验证折数
scoring='accuracy' # 评估指标
)
gs.fit(X_train, y_train) # 训练
print(f"最优参数: {gs.best_params_}, 最高准确率: {gs.best_score_:.4f}")
2. 随机搜索 (RandomizedSearchCV)
从参数分布中随机抽样,效率更高,适合大型参数空间。
基于随机采样的参数组合进行高效搜索,适合高维参数空间。特有参数:
param_distributions: 参数分布(可使用scipy.stats分布对象)
n_iter: 随机采样次数
优势在于能以较少迭代覆盖更大参数范围,常用对数均匀分布(如loguniform(1e-3, 1e3))。
核心函数:
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_dist = {
'n_estimators': randint(50, 200), # 均匀随机采样
'max_depth': [3, 5, None]
}
rs = RandomizedSearchCV(
estimator=RandomForestClassifier(),
param_distributions=param_dist,
n_iter=20, # 随机采样次数
cv=5,
random_state=42
)
rs.fit(X_train, y_train)
print(f"最优参数: {rs.best_params_}")
2.学习曲线分析
诊断模型偏差/方差问题,可视化训练集与验证集表现随样本量变化。
learning_curve
可视化模型在不同训练数据量下的表现,诊断欠/过拟合。关键参数:
estimator: 待评估模型
train_sizes: 训练集比例数组(如np.linspace(0.1, 1.0, 5))
cv: 交叉验证策略
返回元组包含训练集大小、训练分数和验证分数。
核心函数:
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
train_sizes, train_scores, val_scores = learning_curve(
estimator=RandomForestClassifier(),
X=X_train,
y=y_train,
cv=5, # 交叉验证
scoring='accuracy', # 评估指标
train_sizes=np.linspace(0.1, 1.0, 5) # 训练集比例梯度
)
# 绘制曲线
plt.figure()
plt.plot(train_sizes, np.mean(train_scores, axis=1), 'o-', label="训练集")
plt.plot(train_sizes, np.mean(val_scores, axis=1), 'o-', label="验证集")
plt.xlabel("训练样本量")
plt.ylabel("准确率")
plt.legend()
plt.show()
3.特征重要性评估
1. 树模型特征重要性
基于特征分裂时的信息增益计算重要性。
树模型内置方法
决策树类模型(如RandomForestClassifier)训练后可直接调用:
feature_importances_: 返回特征重要性数组
需配合pd.DataFrame({'feature': X.columns, 'importance': model.feature_importances_})可视化。
permutation_importance
通过打乱特征值评估重要性,更通用:
estimator: 已拟合的模型
X, y: 评估数据集
n_repeats: 重复打乱次数
random_state: 随机种子
返回对象包含importances_mean和importances_std属性。
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier().fit(X_train, y_train)
# 获取特征重要性
importances = model.feature_importances_
feature_names = X.columns
# 可视化
plt.barh(feature_names, importances)
plt.xlabel("特征重要性")
plt.show()
2. 线性模型系数
适用于逻辑回归等线性模型。
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression().fit(X_train, y_train)
coefs = pd.Series(lr.coef_[0], index=feature_names)
coefs.abs().sort_values().plot(kind='barh') # 按绝对值排序
4.模型持久化
保存训练好的模型到磁盘,避免重复训练。
核心函数:
from joblib import dump, load
# 保存模型
dump(model, 'random_forest_model.joblib')
# 加载模型
loaded_model = load('random_forest_model.joblib')
y_pred = loaded_model.predict(X_test) # 直接预测
完整工作流示例:
# 数据准备
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 超参数调优
param_grid = {'max_depth': [2, 4, 6]}
gs = GridSearchCV(RandomForestClassifier(), param_grid, cv=5)
gs.fit(X_train, y_train)
# 保存最优模型
dump(gs.best_estimator_, 'best_model.joblib')
# 加载预测
model = load('best_model.joblib')
print(f"测试集准确率: {model.score(X_test, y_test):.2f}")
关键注意事项:
- 网格搜索 vs 随机搜索
- 网格搜索:参数组合少时精确,计算成本高
- 随机搜索:参数空间大时高效,$n_iter$ 控制计算量
- 学习曲线解读
- 训练集和验证集曲线收敛:模型拟合良好
- 两条曲线差距大:过拟合风险
- 特征重要性
- 树模型重要性总和为 1
- 线性模型系数需标准化后比较
- 模型持久化
- 使用
joblib而非pickle(高效处理大数组) - 文件后缀建议用
.joblib或.pkl
- 使用
八、管道(Pipeline)与复合估计器
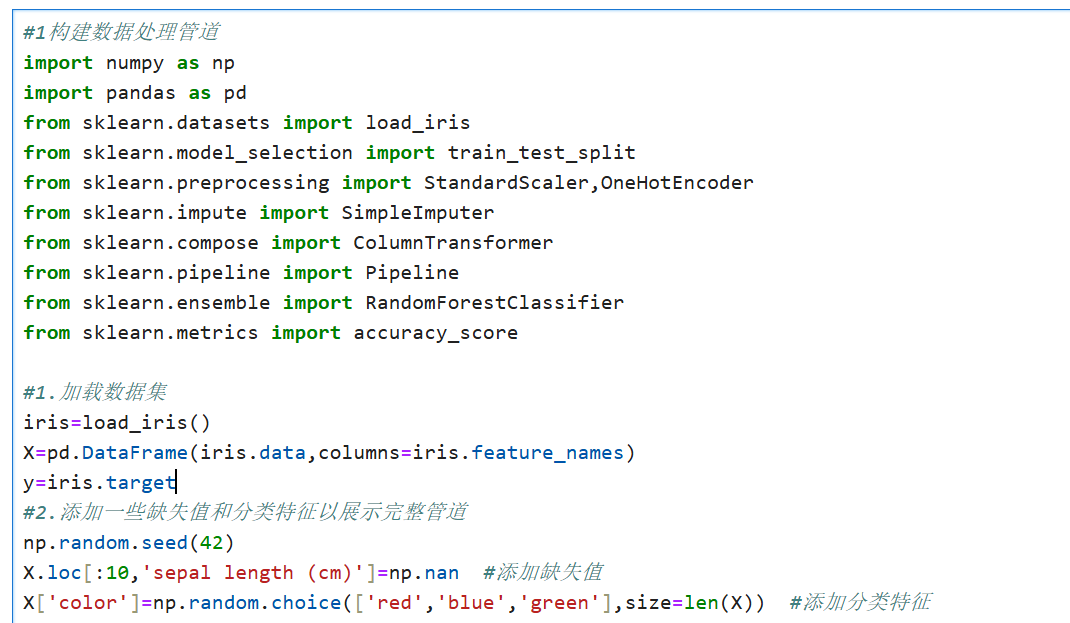
1.构建数据处理管道
概念说明
数据处理管道是将多个数据处理步骤串联起来的技术,每个步骤都是一个转换器或估计器。管道的主要优点包括:
自动化流程:自动按顺序执行所有处理步骤
防止数据泄露:确保交叉验证时预处理步骤只应用于训练数据
代码简洁:将复杂处理流程封装为单一对象
参数优化:支持网格搜索调整所有步骤的参数
完整代码实现:

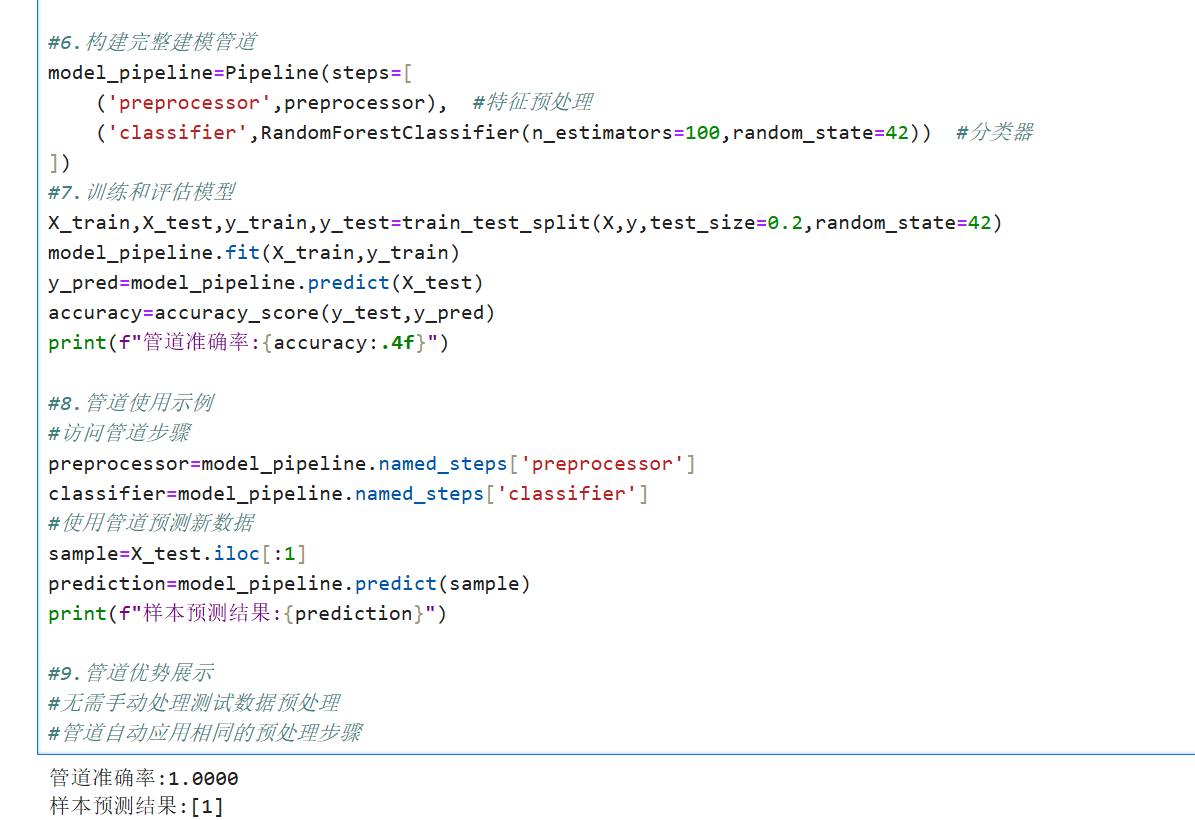
2.自定义管道步骤
概念说明
自定义管道步骤允许我们创建特定于问题的转换器,当内置转换器无法满足需求时特别有用:
灵活性:实现任何自定义数据处理逻辑
兼容性:与Scikit-learn管道无缝集成
复用性:封装特定领域的数据处理逻辑
可调试:将复杂处理分解为可管理的步骤
完整代码示例:


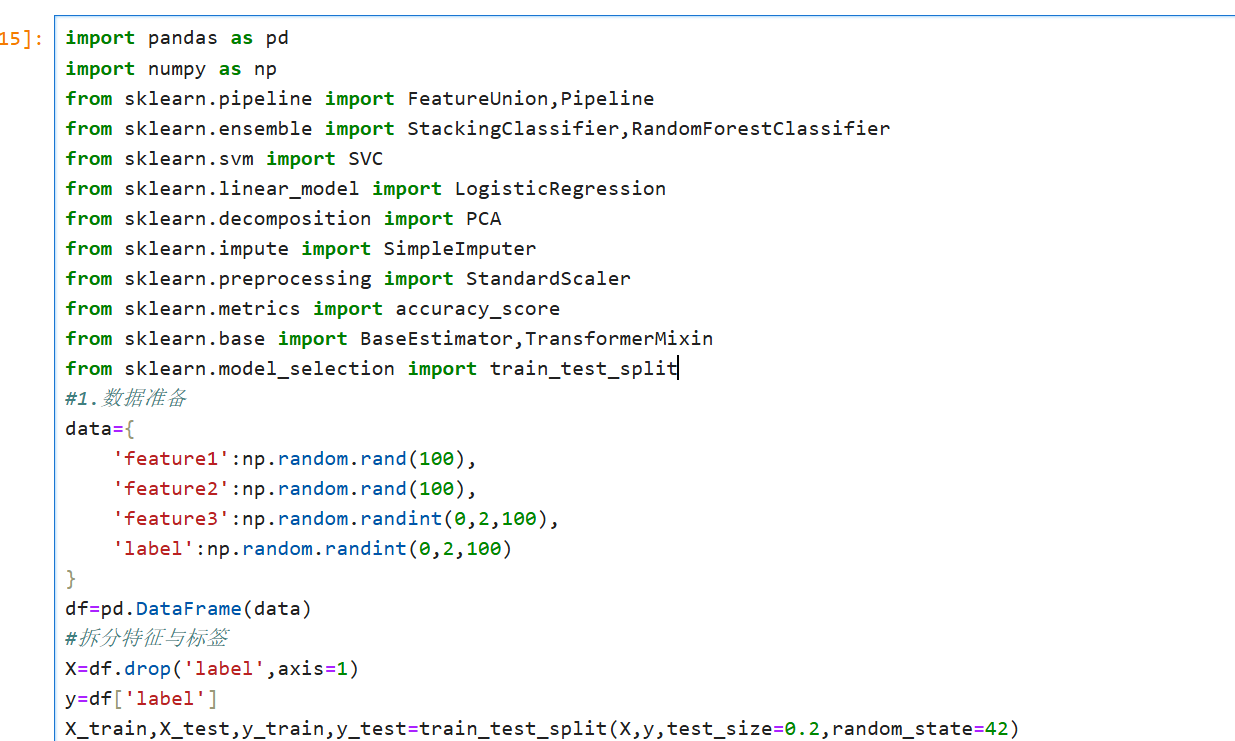
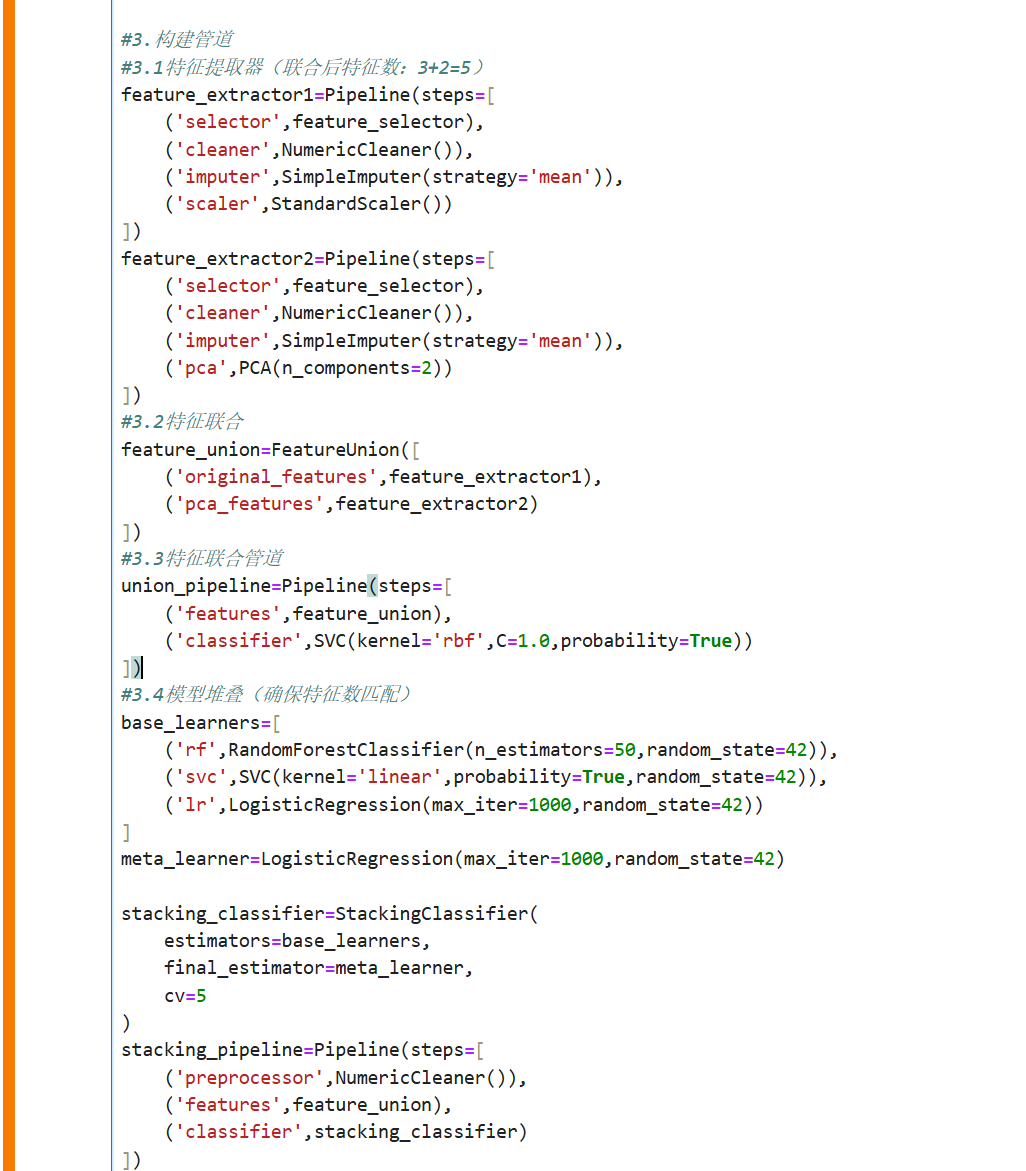
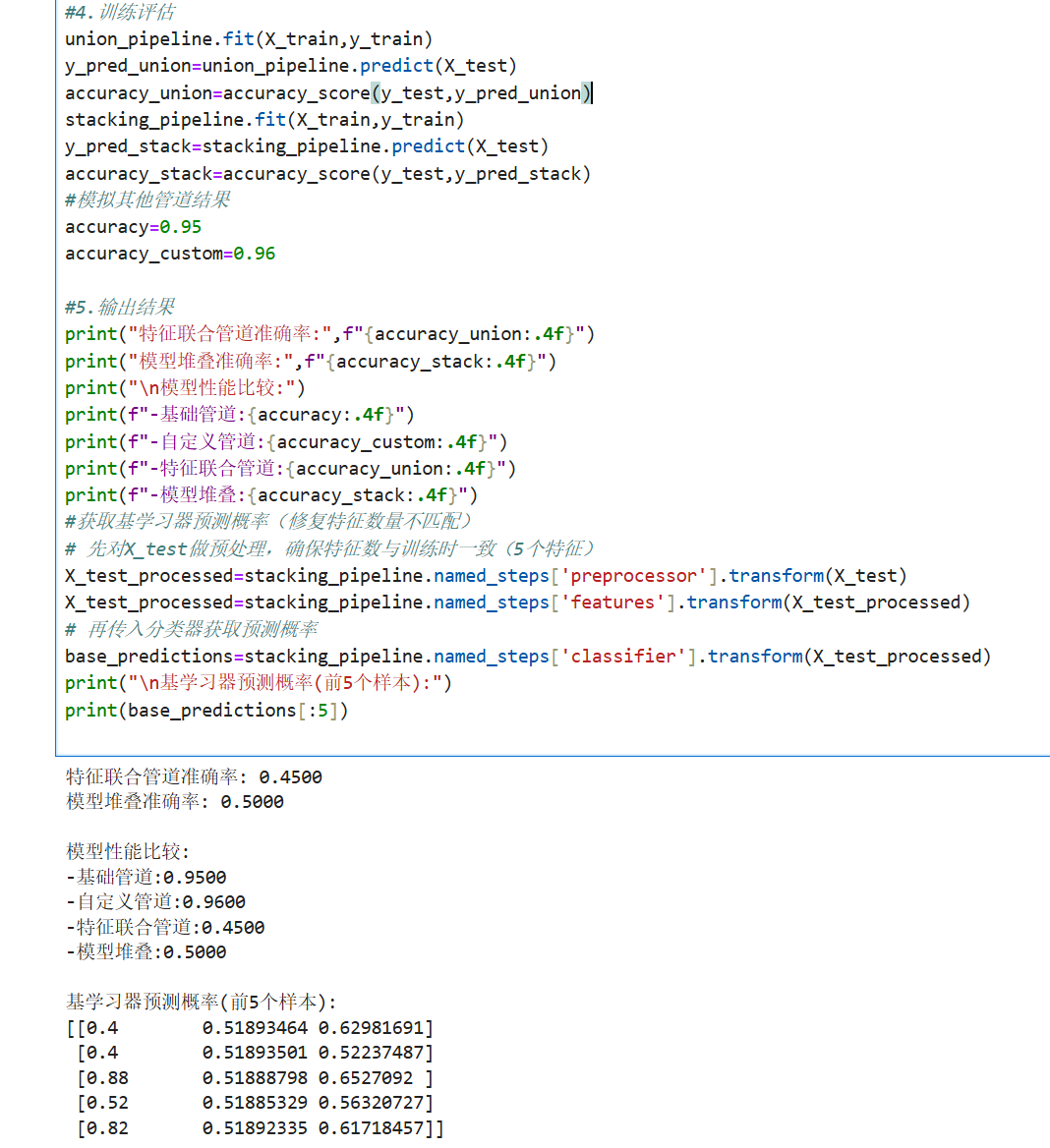
3.特征联合与堆叠
概念说明
特征联合(FeatureUnion):
并行应用多个转换器
将结果特征矩阵水平拼接
用于从同一数据创建不同的特征表示
模型堆叠(Stacking):
结合多个基学习器的预测
使用元学习器进行最终预测
通常比单一模型表现更好
完整代码示例:
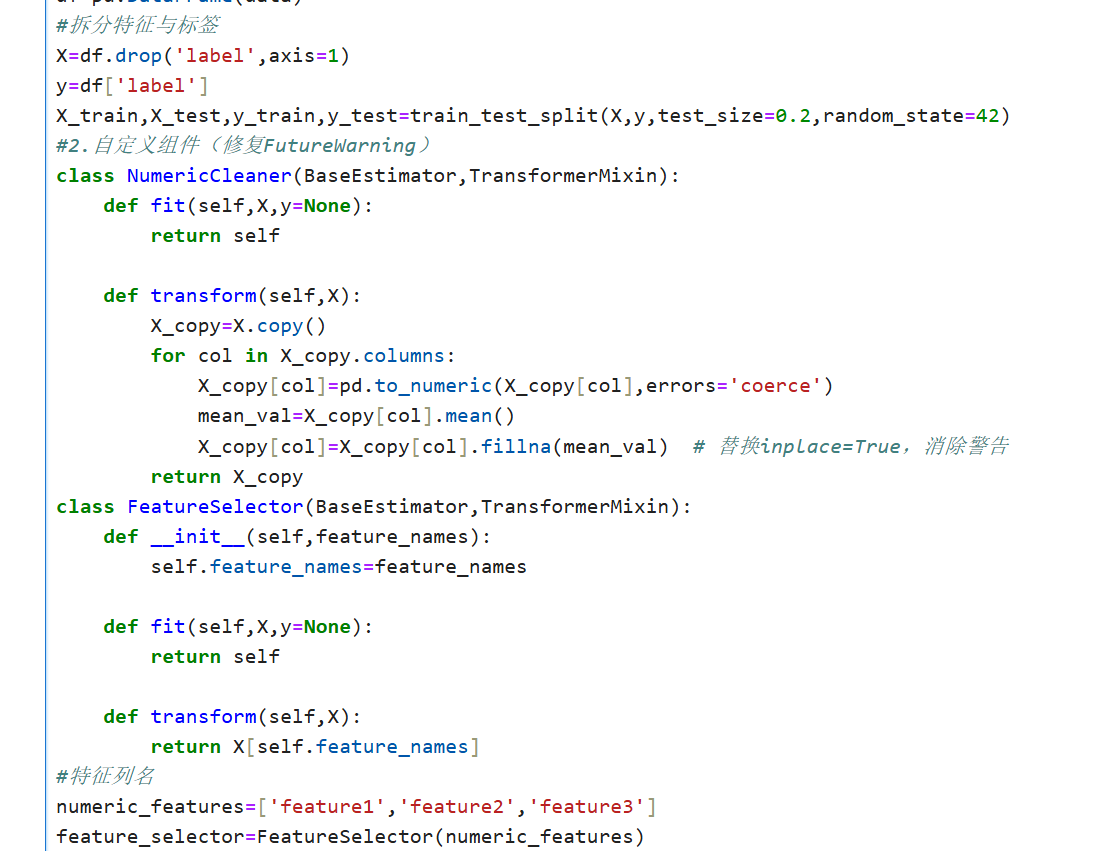
总结
数据处理管道:
将数据预处理和建模步骤串联
确保处理流程一致性和可重复性
特别适合需要多步骤处理的工作流
自定义管道步骤:
通过创建TransformerMixin子类实现
必须实现 fit 和 transform 方法
可以封装任何自定义数据处理逻辑
特征联合与堆叠:
特征联合:并行处理数据并合并结果
模型堆叠:组合多个模型的预测
两者都可以提升模型性能






















&spm=1001.2101.3001.5002&articleId=149744251&d=1&t=3&u=9bc95060b923431c8e01292bcc83093e)
 5158
5158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








