目录
最大公约数(Greatest Common Divisor, GCD)
最小公倍数(Least Common Multiple, LCM)
一、数组numpy的使用
1.入门python数组
NumPy 是一个 Python 库。
NumPy 用于处理数组。NumPy 是 "Numerical Python" 的缩写。
什么是 NumPy?
NumPy 是一个用于处理数组的 Python 库。
它还包含用于线性代数、傅里叶变换和矩阵领域的函数。
为什么 NumPy 比列表更快?
NumPy 数组存储在内存中的一个连续位置,与列表不同,因此进程可以非常高效地访问和操作它们。
NumPy 是一个 Python 库,部分是用 Python 编写的,但大部分需要快速计算的部分是用 C 或 C++ 编写的。
NumPy的源代码位于这个 github 存储库 https://github.com/numpy/numpy
安装NumPy:pip install numpy

2.数组索引
创建多维数组
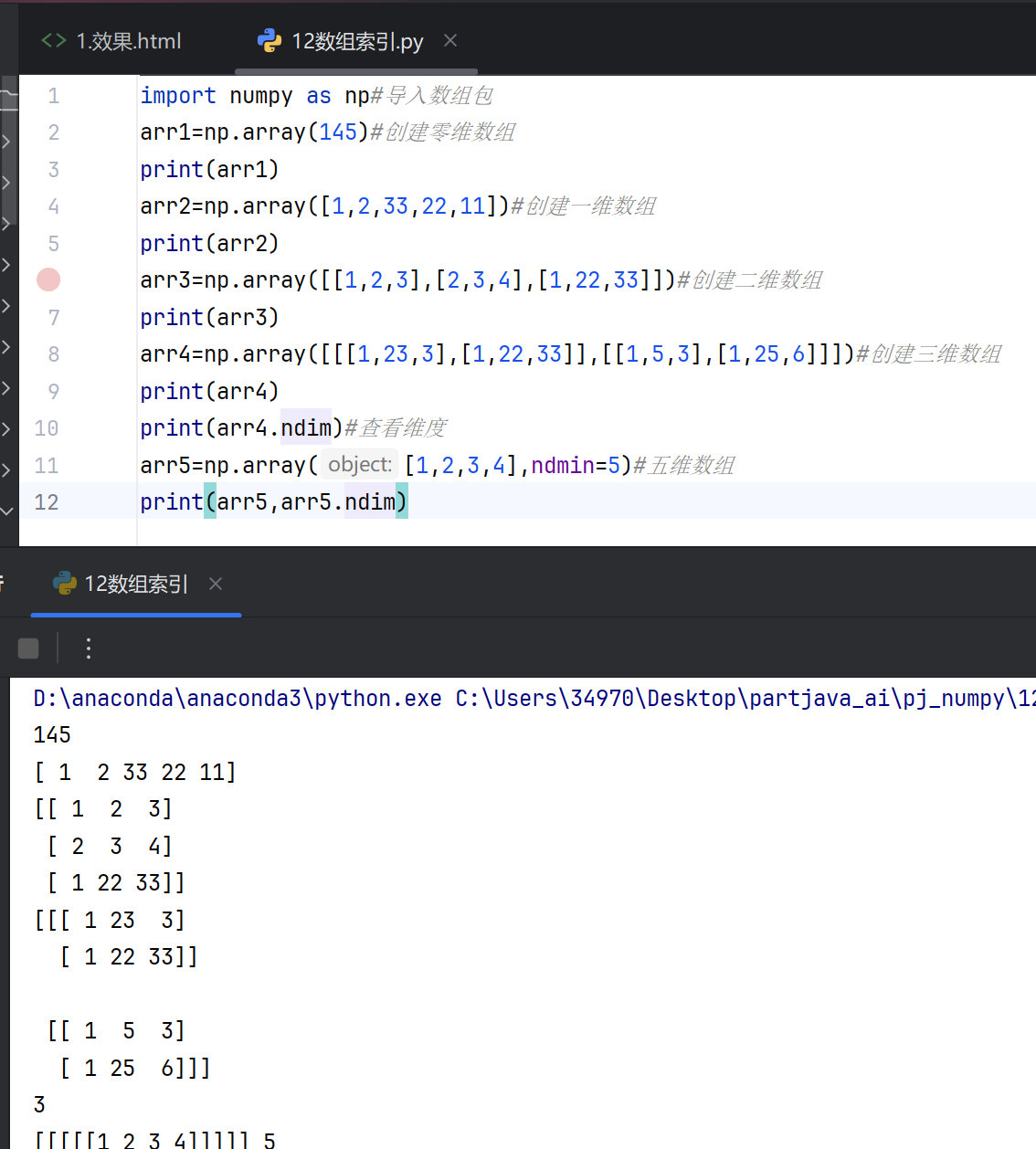
数组各个索引
第一个元素的索引为 0,第二个元素的索引为 1,依此类推。
访问二维数组
要访问二维数组中的元素,我们可以使用逗号分隔的整数来表示元素的维度和索引。
将二维数组想象成带有行和列的表格,其中维度代表行,索引代表列。
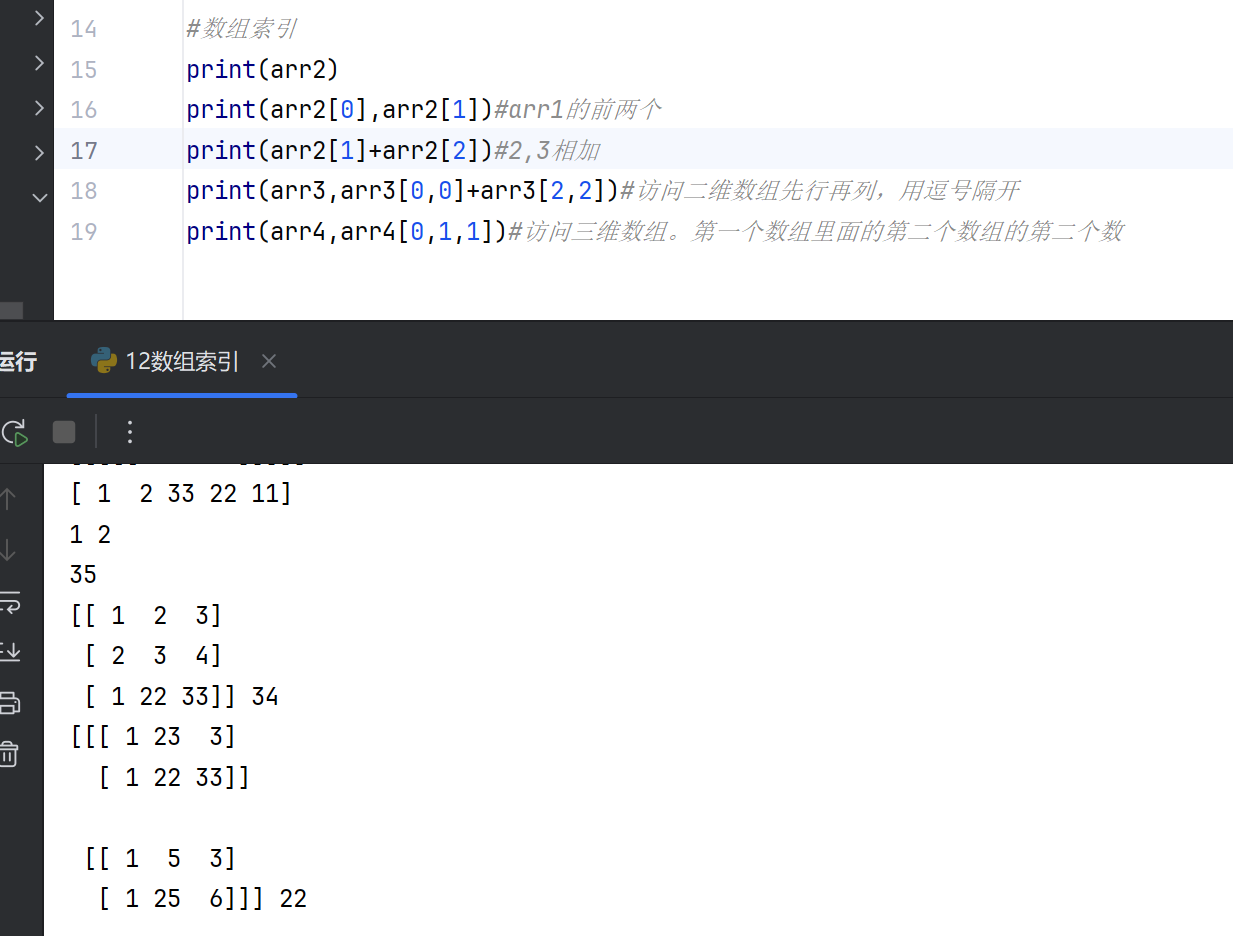
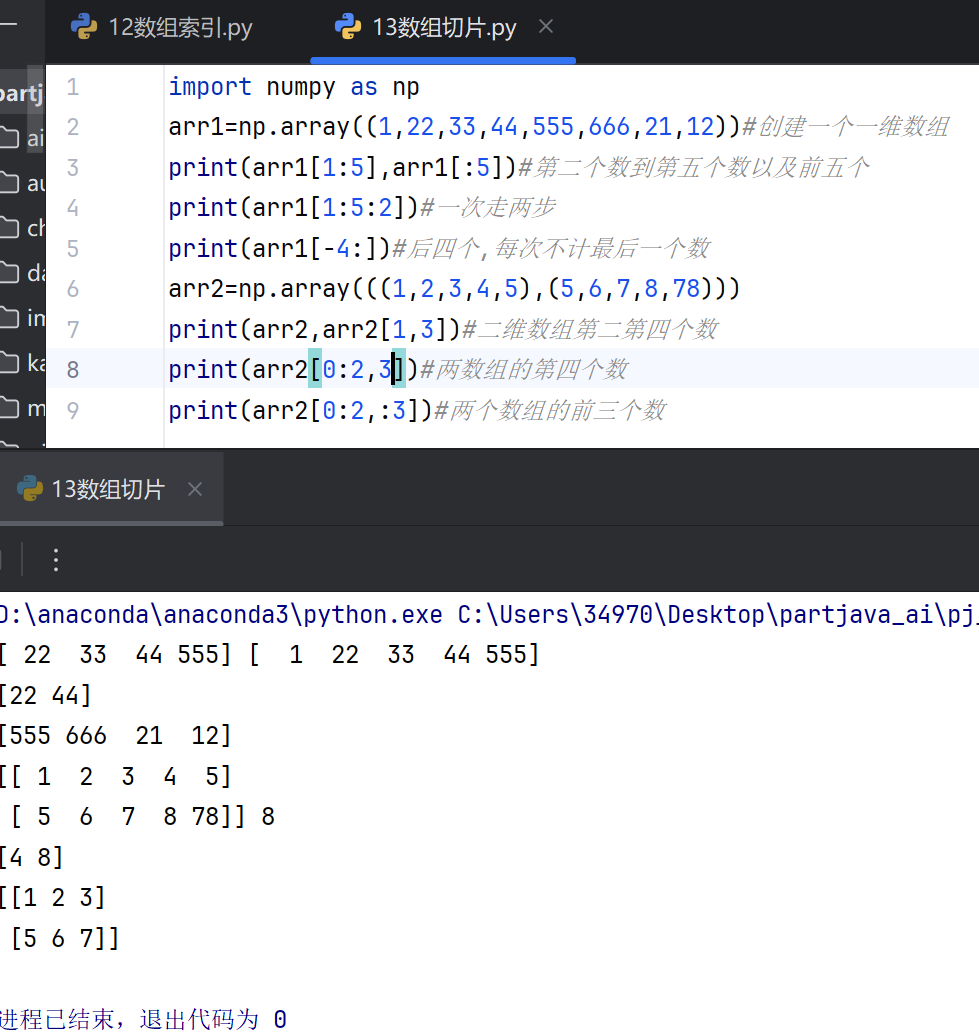
3.数组切片
在 Python 中,切片意味着从一个给定的索引到另一个给定的索引中取出元素。
我们像这样传递切片而不是索引:[start:end]。
我们还可以定义步长,像这样:[start:end:step]。
如果我们不传递 start,它被视为 0。
如果我们不传递 end,它被视为该维度数组的长度。
如果我们不传递 step,它被视为 1。
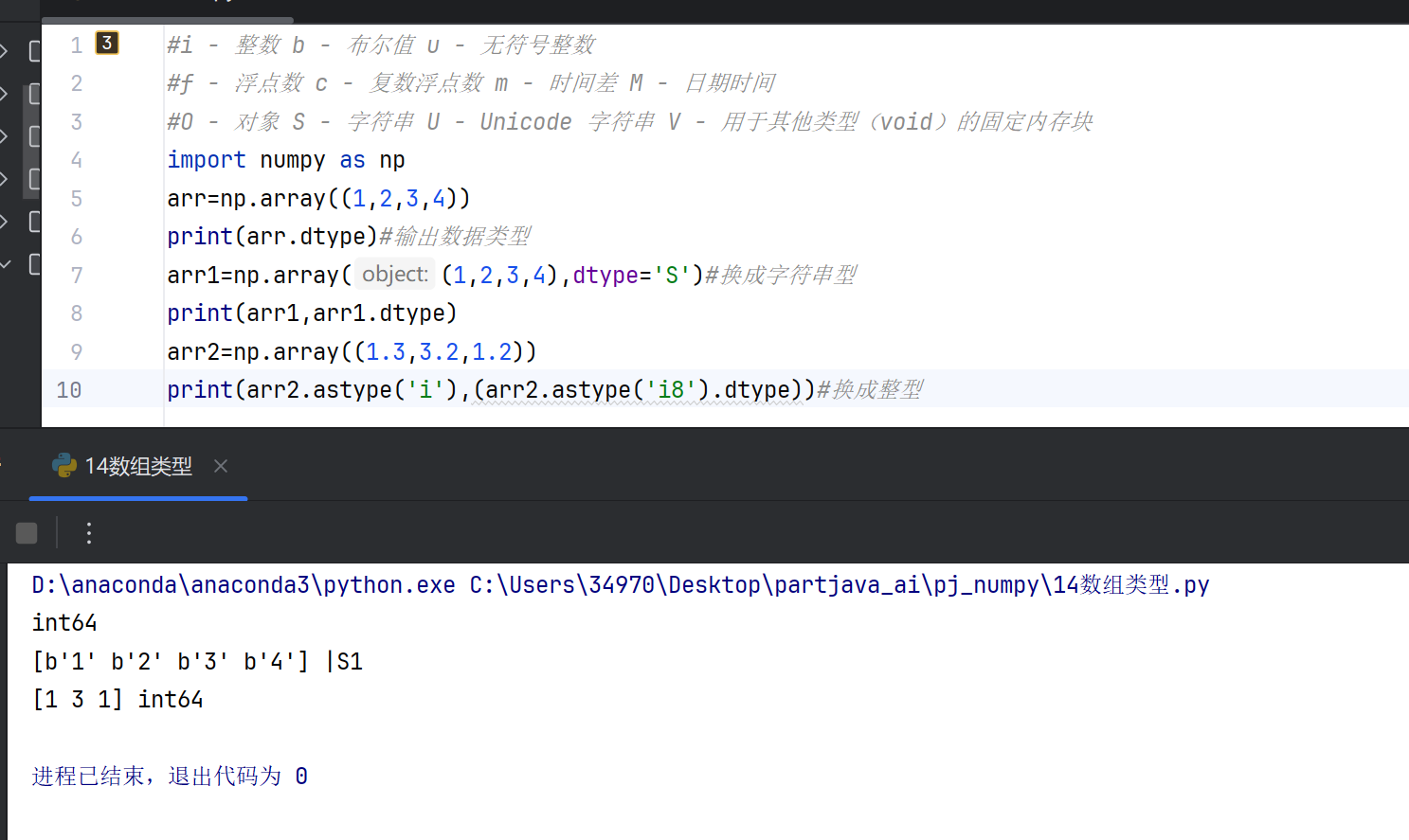
4.数组数据类型
精简版 NumPy 数据类型表
| 数据类型 | 描述 | 内存占用 | 典型取值范围 |
|---|---|---|---|
np.int8 | 8位有符号整数 | 1字节 | -128 ~ 127 |
np.uint8 | 8位无符号整数 | 1字节 | 0 ~ 255 |
np.int32 | 32位有符号整数 | 4字节 | -2.1e9 ~ 2.1e9 |
np.float32 | 单精度浮点数 | 4字节 | ±1.2e-38 ~ ±3.4e38 |
np.float64 | 双精度浮点数 | 8字节 | ±2.2e-308 ~ ±1.8e308 |
np.bool_ | 布尔值 | 1字节 | True/False |
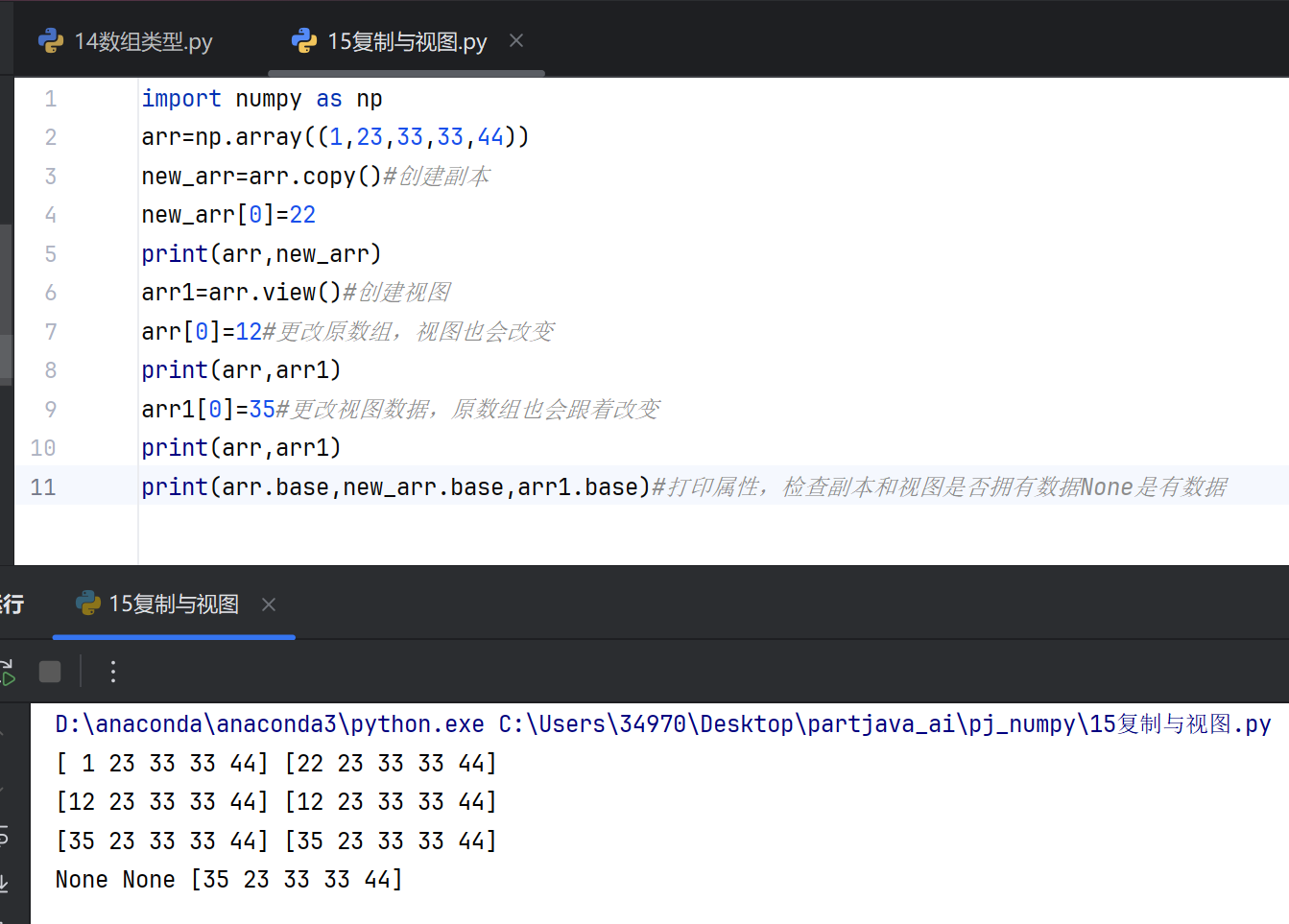
5.复制与视图
复制:创建数组的独立副本,修改副本不会影响原始数组。
视图:创建数组的共享数据引用,修改视图会影响原始数组。
6.形状重塑迭代
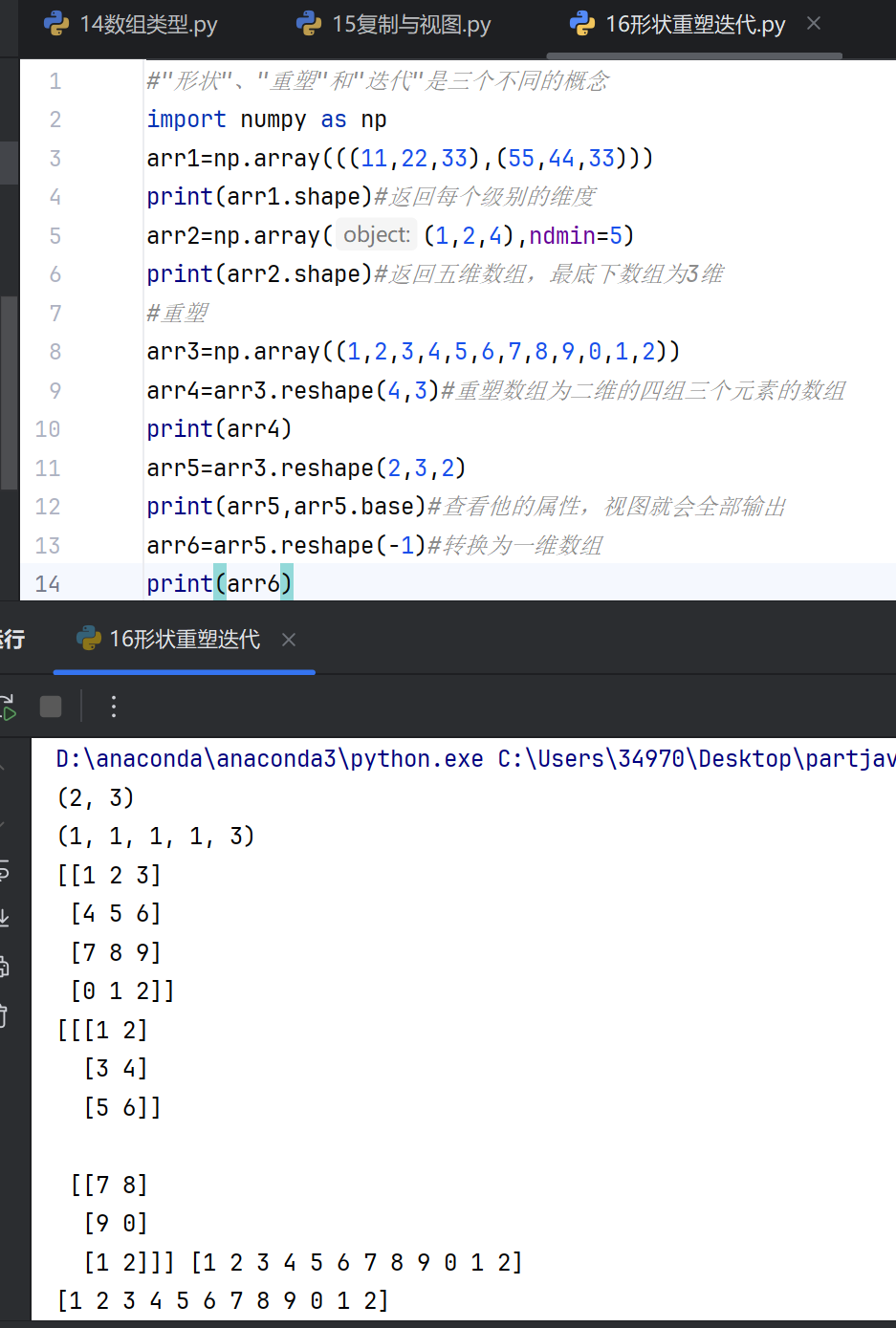
在编程和数据处理中,"形状"、"重塑"和"迭代"是三个不同的概念,以下是它们的区别和解释:
形状(Shape)
形状通常指数据结构(如数组、矩阵)的维度信息。例如,在NumPy中,shape属性返回一个元组,表示数组在每个维度上的大小。一个3行4列的矩阵,其shape为(3,4)。形状是数据结构的静态属性,描述其组织形式。
重塑(Reshape)
重塑是指改变数据结构的形状而不改变其数据内容。例如,将一个12元素的1维数组重塑为3行4列的2维数组。在NumPy中,使用reshape方法实现。重塑操作需保证原始数据元素总数与新形状一致,否则会报错。
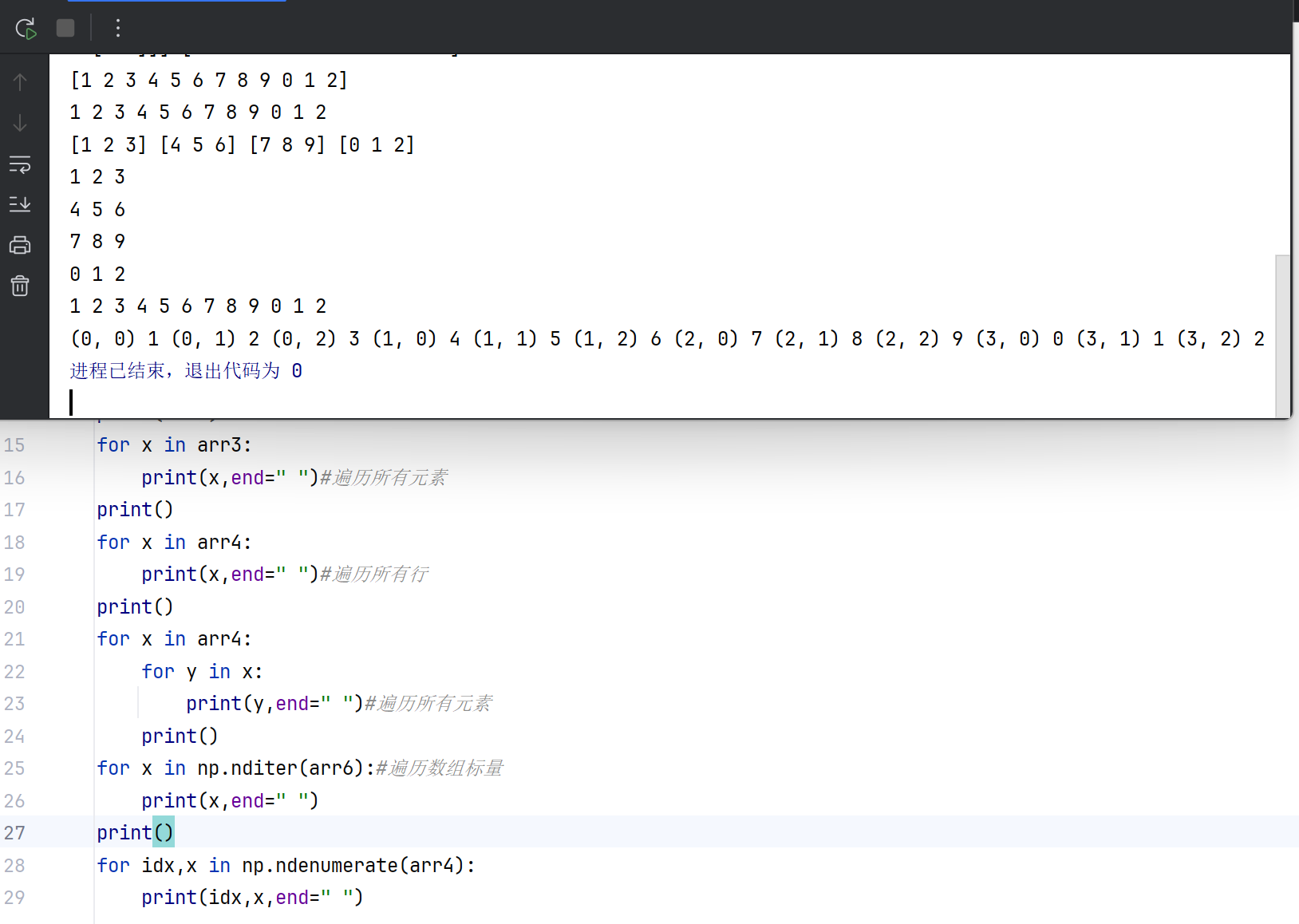
迭代(Iteration)
迭代是指按顺序访问数据结构中的每个元素。对于多维数组,迭代可以按行、按列或按元素进行。迭代是一种动态操作过程,常用于循环处理数据。
12元素的1维数组重塑为3行4列的2维数组。在NumPy中,使用reshape方法实现。重塑操作需保证原始数据元素总数与新形状一致,否则会报错。
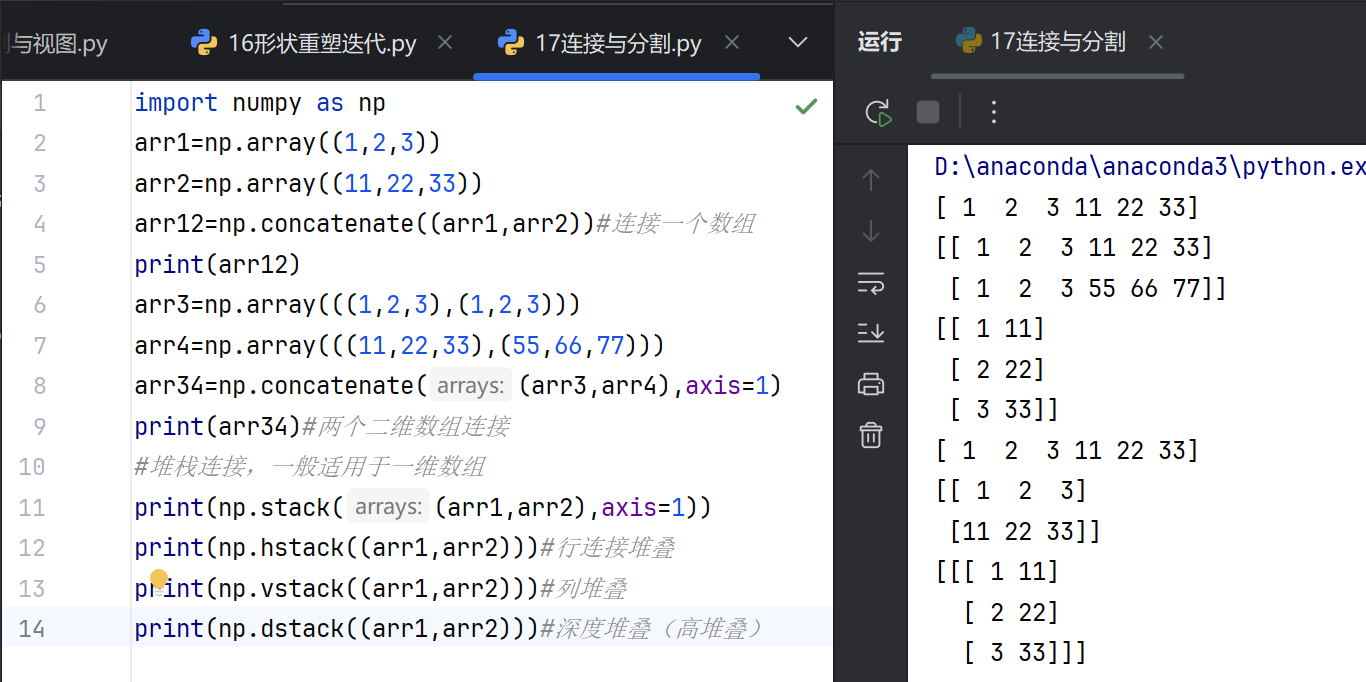
7.连接与分割
在 SQL 中,我们基于键来连接表,而在 NumPy 中,我们通过轴来连接数组。
连接两个一维数组,这将导致它们一个接一个地放置,即堆叠。

8.搜索排序过滤
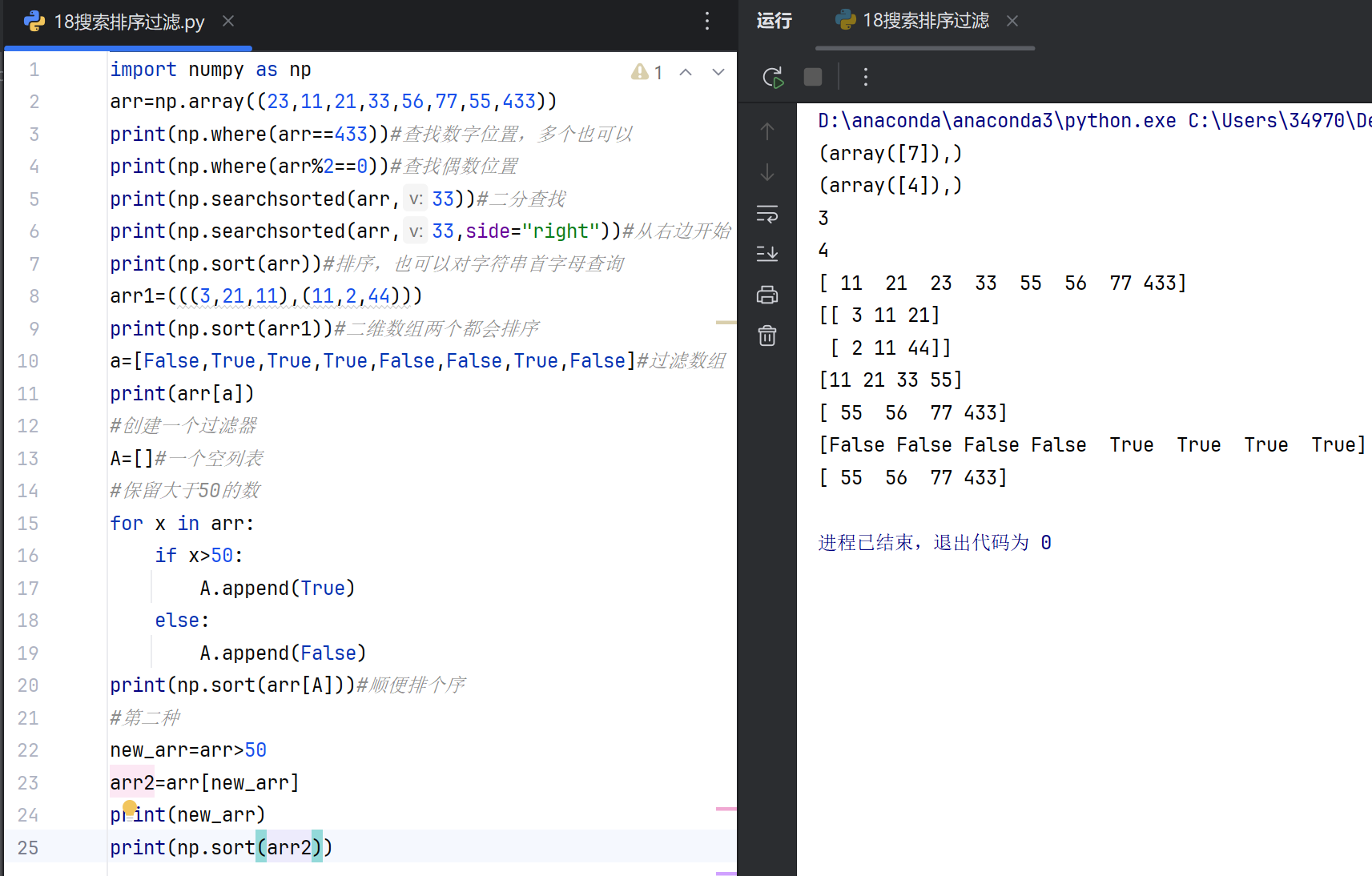
搜索(Searching)
在NumPy中,搜索通常指在数组中查找特定元素或满足条件的元素。常用函数包括np.where()和np.searchsorted()。np.where()返回满足条件的索引,np.searchsorted()在已排序数组中查找插入位置以维持有序性。
排序(Sorting)
排序指对数组元素进行升序或降序排列。NumPy提供np.sort()返回排序后的数组副本,np.argsort()返回排序后的索引,np.lexsort()用于多键排序。这些函数支持沿指定轴操作。
过滤(Filtering)
过滤指从数组中提取满足特定条件的元素。常用方法包括布尔索引(如arr[arr > 5])和np.extract()函数。布尔索引直接通过条件筛选,np.extract()从扁平化数组中提取符合条件的元素。
二、数学公式的使用
1.随机数与数据分布
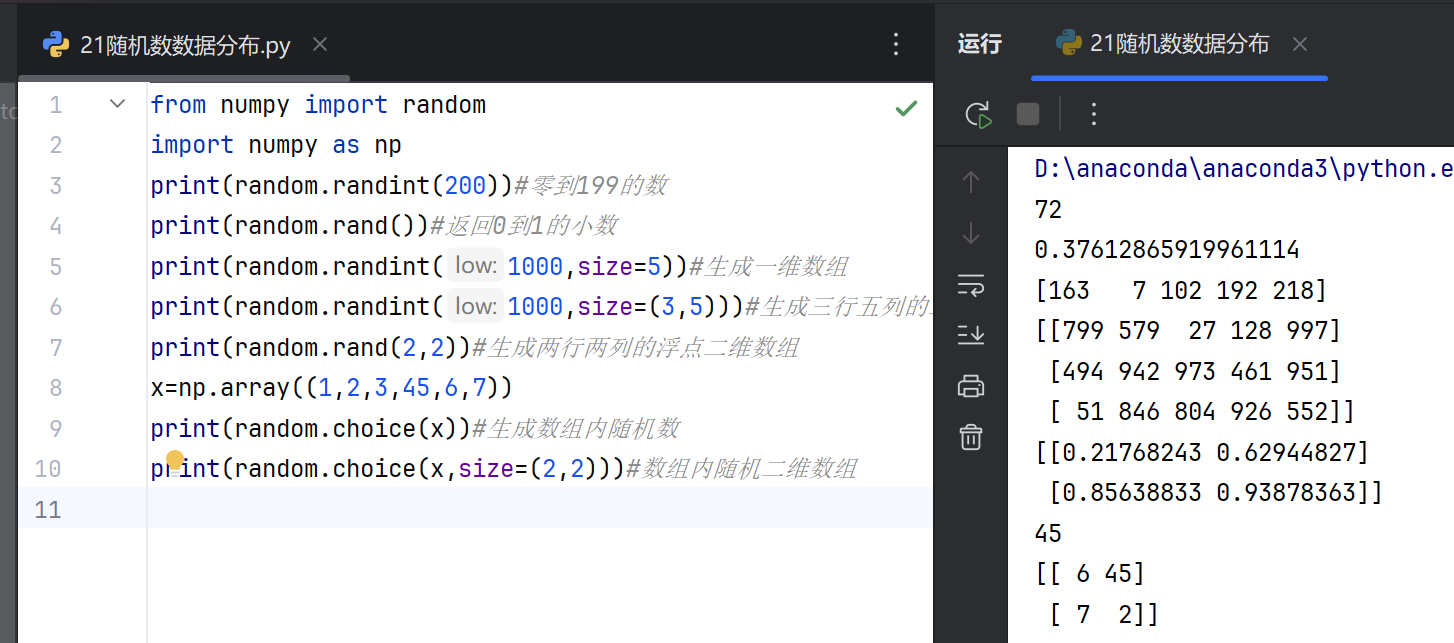
随机数生成
NumPy的random模块提供了多种随机数生成方法,用于生成不同分布的随机数。基础随机数生成包括均匀分布和标准正态分布。
np.random.rand():生成[0,1)区间内的均匀分布随机浮点数。np.random.randn():生成标准正态分布(均值为0,标准差为1)的随机数。np.random.randint():生成指定范围内的随机整数。
常见数据分布
NumPy支持多种概率分布,以下为几种典型分布:
- 均匀分布(Uniform):
np.random.uniform(low, high, size),在指定区间内均匀采样。 - 正态分布(Normal):
np.random.normal(loc, scale, size),可指定均值(loc)和标准差(scale)。 - 泊松分布(Poisson):
np.random.poisson(lam, size),参数lam为事件发生率。 - 二项分布(Binomial):
np.random.binomial(n, p, size),n为试验次数,p为成功概率。

2.随机排列与seaborn
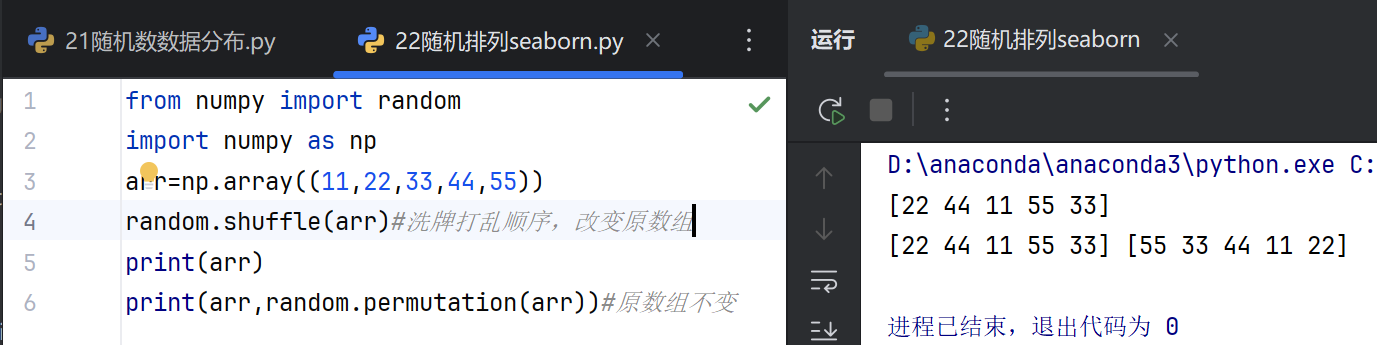
NumPy随机排列
在NumPy中,随机排列功能主要用于生成随机序列或对现有数组进行随机重排。该操作不改变数组内容,仅改变元素的顺序。常用于数据洗牌、模拟实验或避免模型训练中的顺序偏差。
numpy.random.permutation函数接受整数或数组作为输入。输入整数N时,生成0到N-1的随机排列序列;输入数组时,返回数组元素的随机排列副本,原数组保持不变。
numpy.random.shuffle函数直接修改原数组顺序,无返回值。该操作在原位进行,适用于需要节省内存的大规模数据集处理。注意其与permutation的本质区别在于是否改变原始数据。
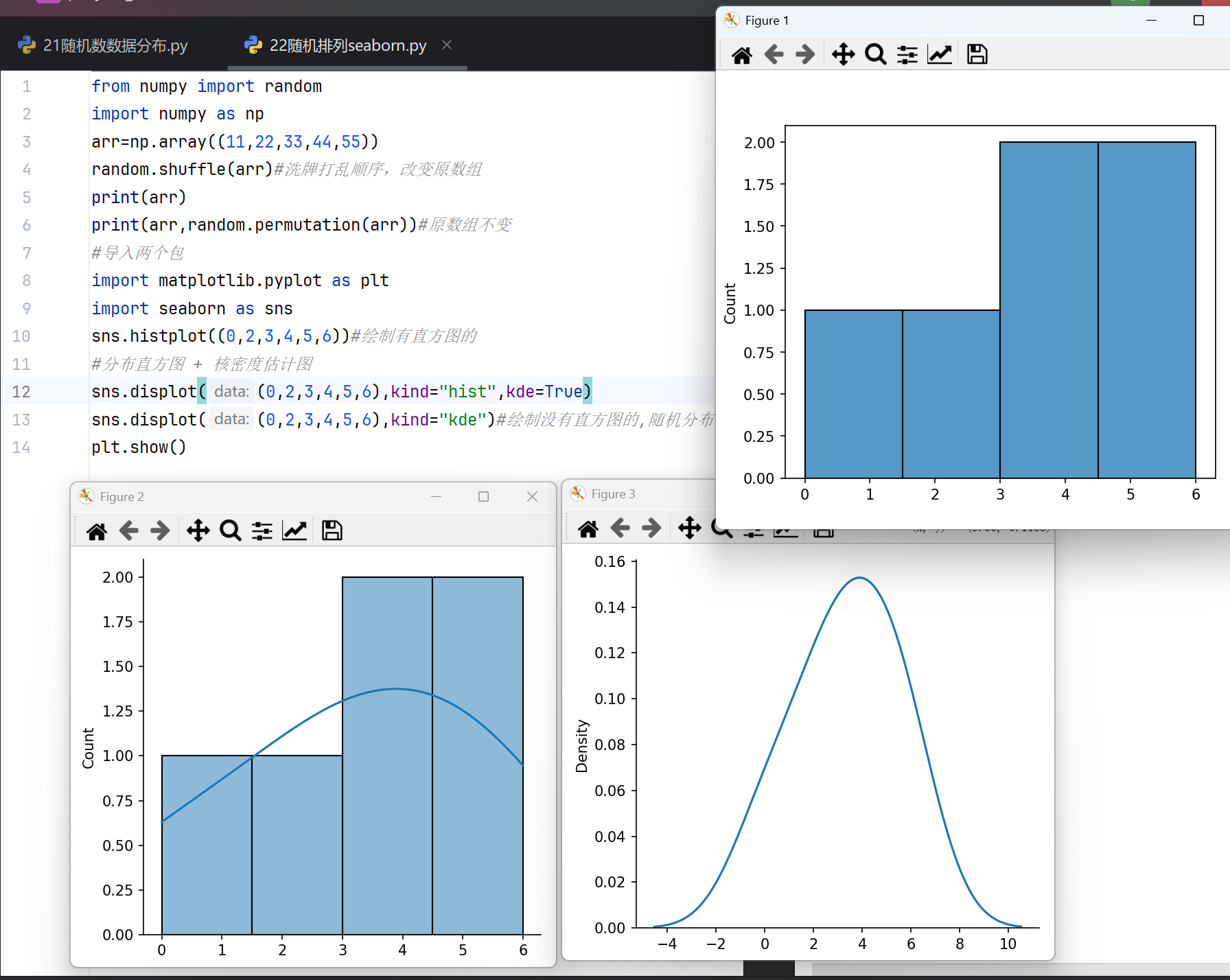
Seaborn可视化
Seaborn作为基于Matplotlib的统计可视化库,提供更高级的接口和美观的默认样式。其特色在于轻松绘制统计关系图、分类分布图和矩阵热力图,内置调色板系统支持自动配色方案。
内置统计聚合功能可自动计算误差线、置信区间和回归线。分面绘图系统通过FacetGrid实现多子图联动,支持基于数据分类变量的自动分面展示。颜色映射系统包含分类调色板、连续调色板和发散调色板三大类型,支持HSLuv空间转换。
高级图表类型包括小提琴图展示分布密度,热力图呈现矩阵数据,配对图实现多变量关系分析。主题风格系统提供五种预设样式,可全局控制字体、背景色和网格线等元素。
如果系统上已安装 Python 和 PIP,请使用以下命令安装 Seaborn:C:\Users\Your Name>pip install seaborn
如果您使用 Jupyter,请使用以下命令安装 Seaborn:C:\Users\Your Name>!pip install seaborn
3.高斯(正态)、二项和泊松分布
高斯分布(正态分布)
在NumPy中,高斯分布(即正态分布)相关的函数主要涉及随机数生成和概率密度计算。
numpy.random.normal
用于生成服从正态分布的随机数。参数包括均值(loc)、标准差(scale)和输出形状(size)。
numpy.random.randn
生成标准正态分布(均值=0,标准差=1)的随机数数组。
numpy.random.standard_normal
类似randn,但支持更灵活的输入形状。
numpy.fft.fft
虽然主要用于傅里叶变换,但在信号处理中常与高斯滤波结合使用。
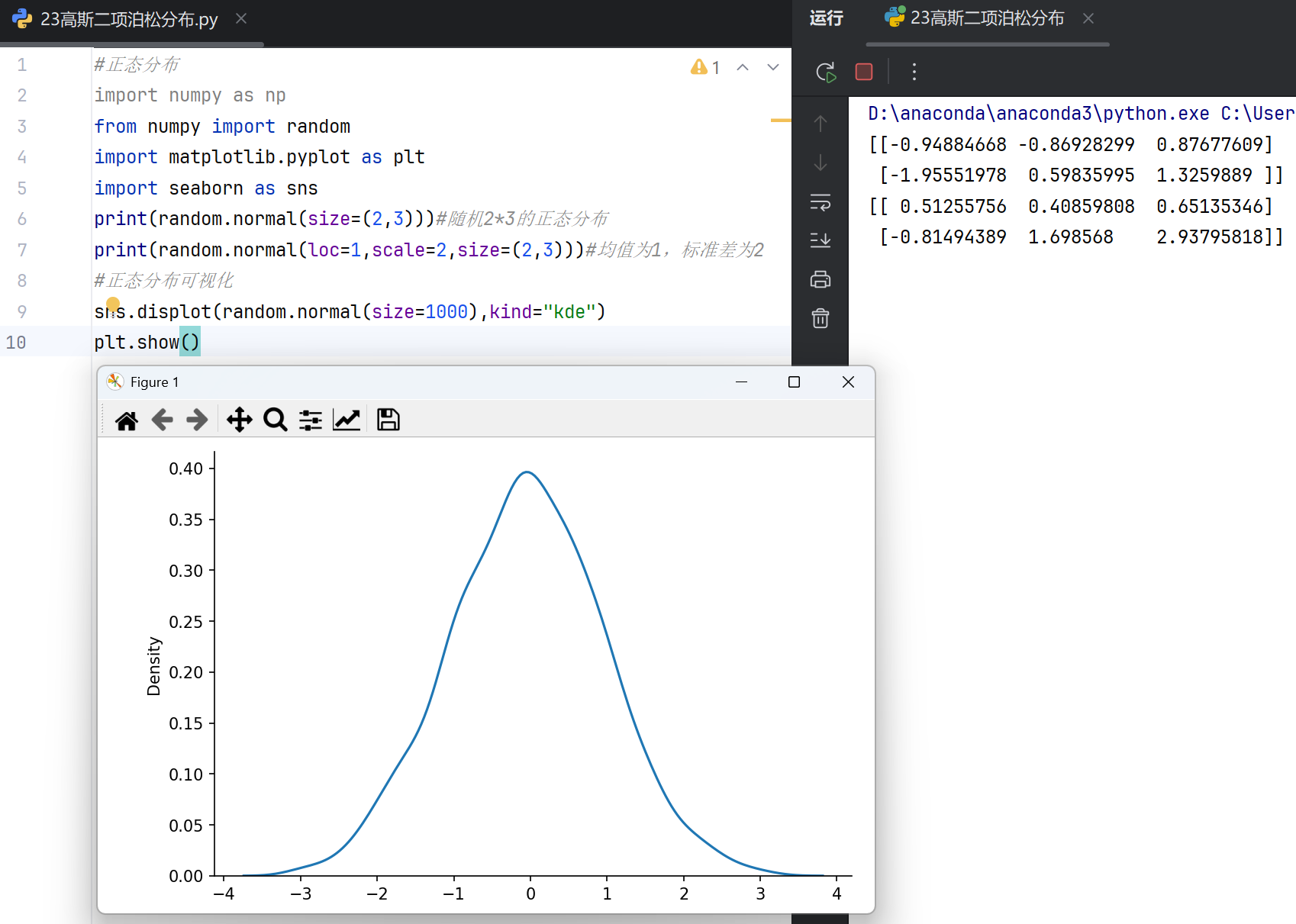
正态分布(高斯分布)的概率计算
NumPy本身不直接提供概率密度函数(PDF)或累积分布函数(CDF),但可与scipy.stats结合使用。若仅限NumPy,可通过以下方式近似:
numpy.exp 和 numpy.sqrt
用于手动计算正态分布的概率密度公式:
numpy.histogram
结合正态分布参数可生成近似概率分布直方图。
二项分布
二项分布涉及重复独立试验的成功概率,NumPy提供以下函数:
numpy.random.binomial
生成二项分布的随机数。参数包括试验次数(n)、成功概率(p)和输出形状(size)。
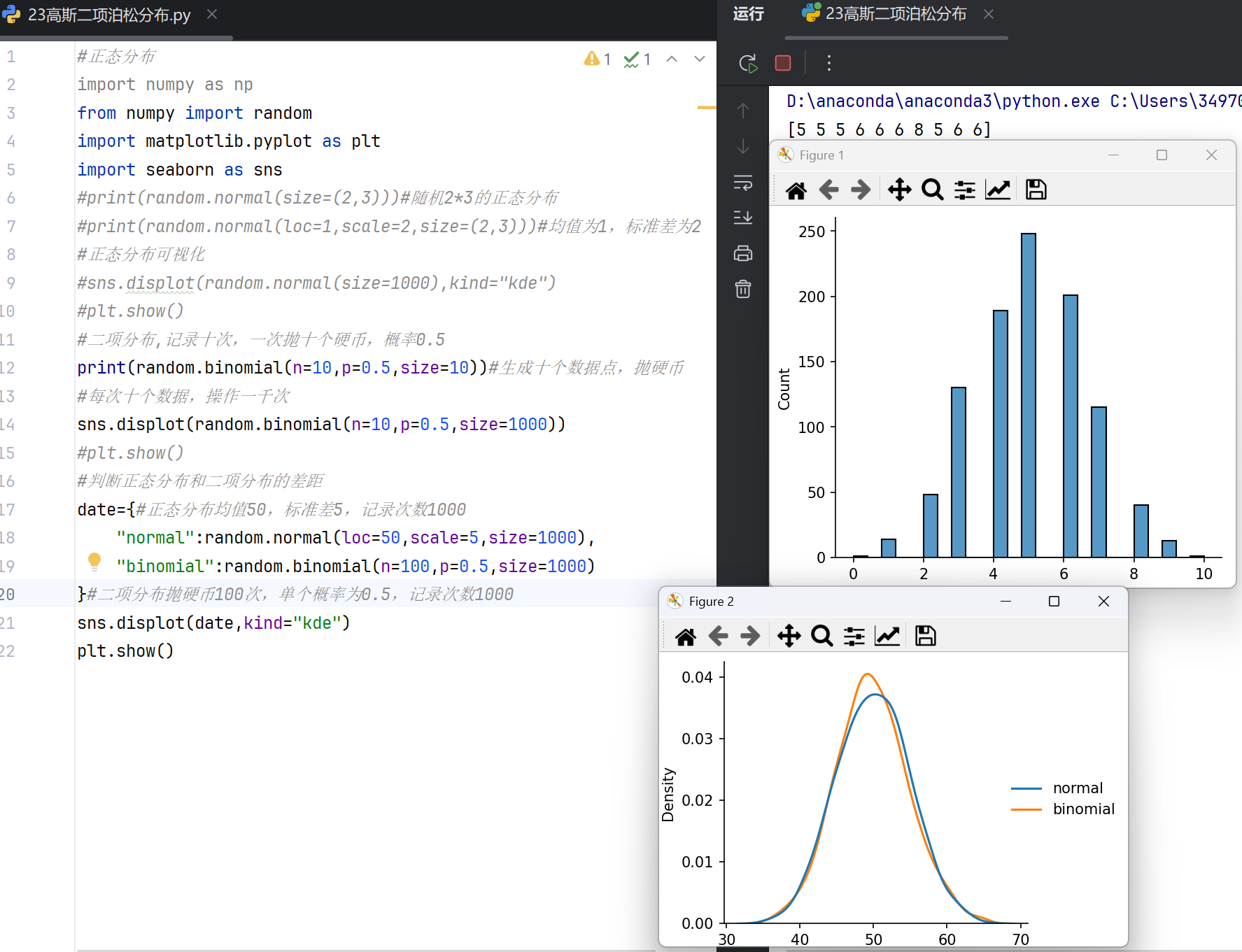
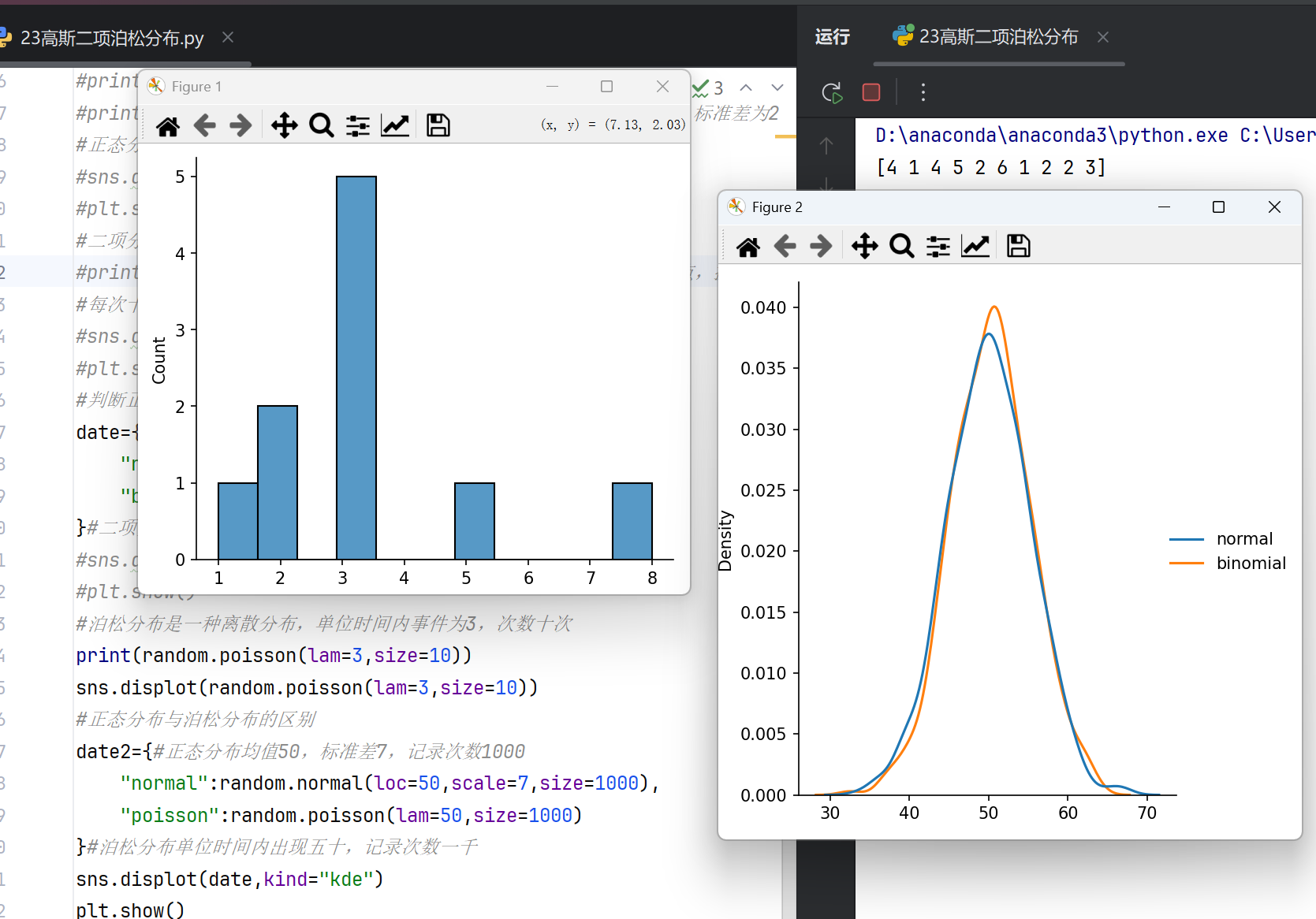
泊松分布的概念
泊松分布是一种离散概率分布,常用于描述单位时间或空间内随机事件发生的次数。其概率质量函数为:
P(X=k) = (λ^k * e^(-λ)) / k!
其中λ为事件发生的平均速率,k为实际发生次数。
NumPy相关函数
numpy.random.poisson:生成泊松分布随机数,参数lam对应λ(事件平均发生率),size控制输出数组形状。
numpy.poisson.pmf:计算泊松分布概率质量函数,需配合scipy.stats模块使用,参数k为发生次数,mu同λ。
numpy.poisson.cdf:计算累积分布函数,返回随机变量小于等于某值的概率。
泊松分布适用于稀有事件建模,如电话呼叫次数、网站访问量等场景。λ越大,分布越接近正态分布。
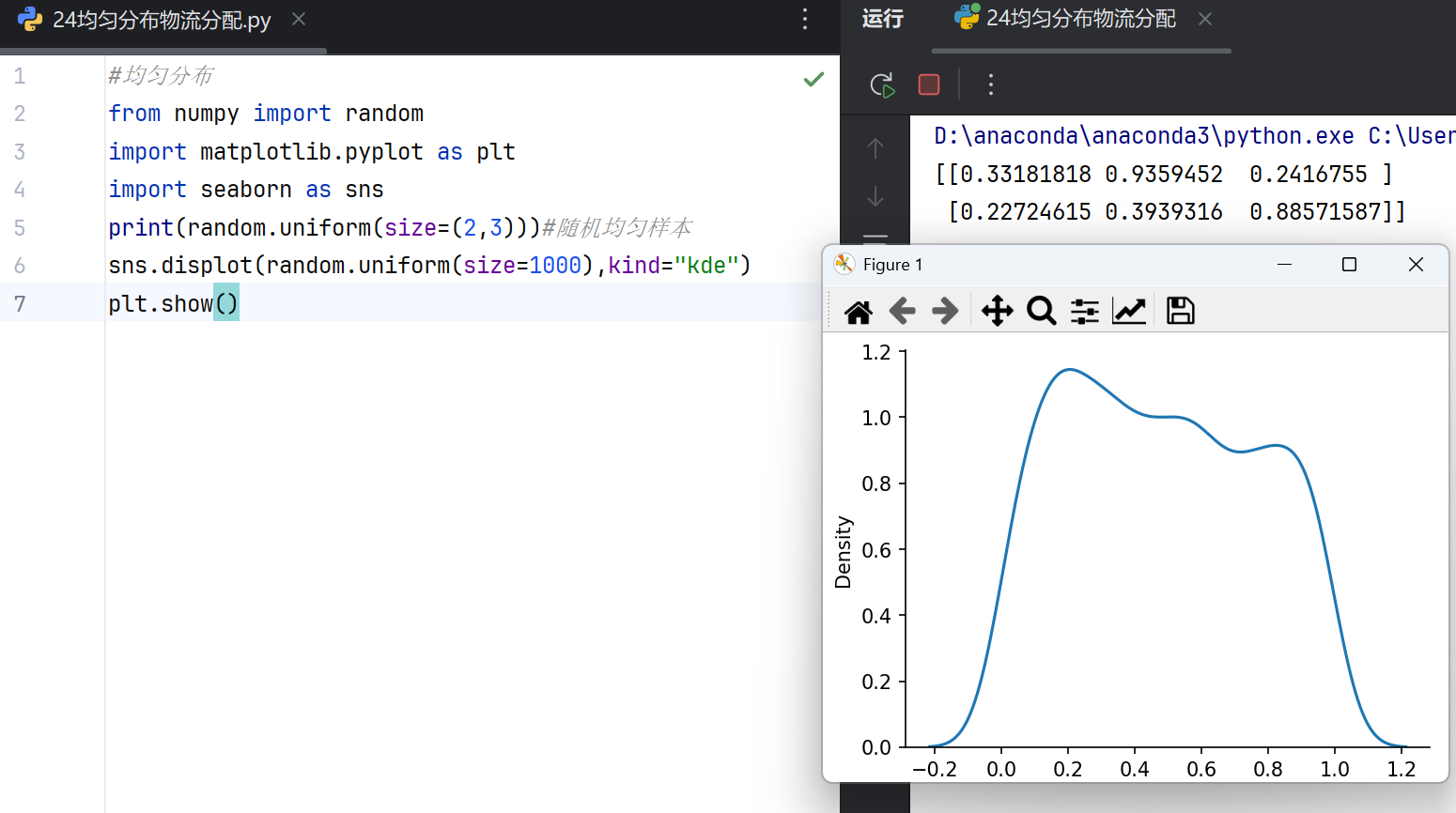
4.均匀分布与物流配送
均匀分布
NumPy中的均匀分布函数用于生成指定区间内均匀分布的随机数。主要函数如下:
numpy.random.uniform:生成在给定区间内均匀分布的随机数。参数包括下限、上限和输出形状。默认区间为[0, 1)。
numpy.random.rand:生成[0, 1)区间内均匀分布的随机数数组,参数仅需指定输出形状。
numpy.random.randint:生成离散均匀分布的随机整数,参数包括下限、上限和输出形状。
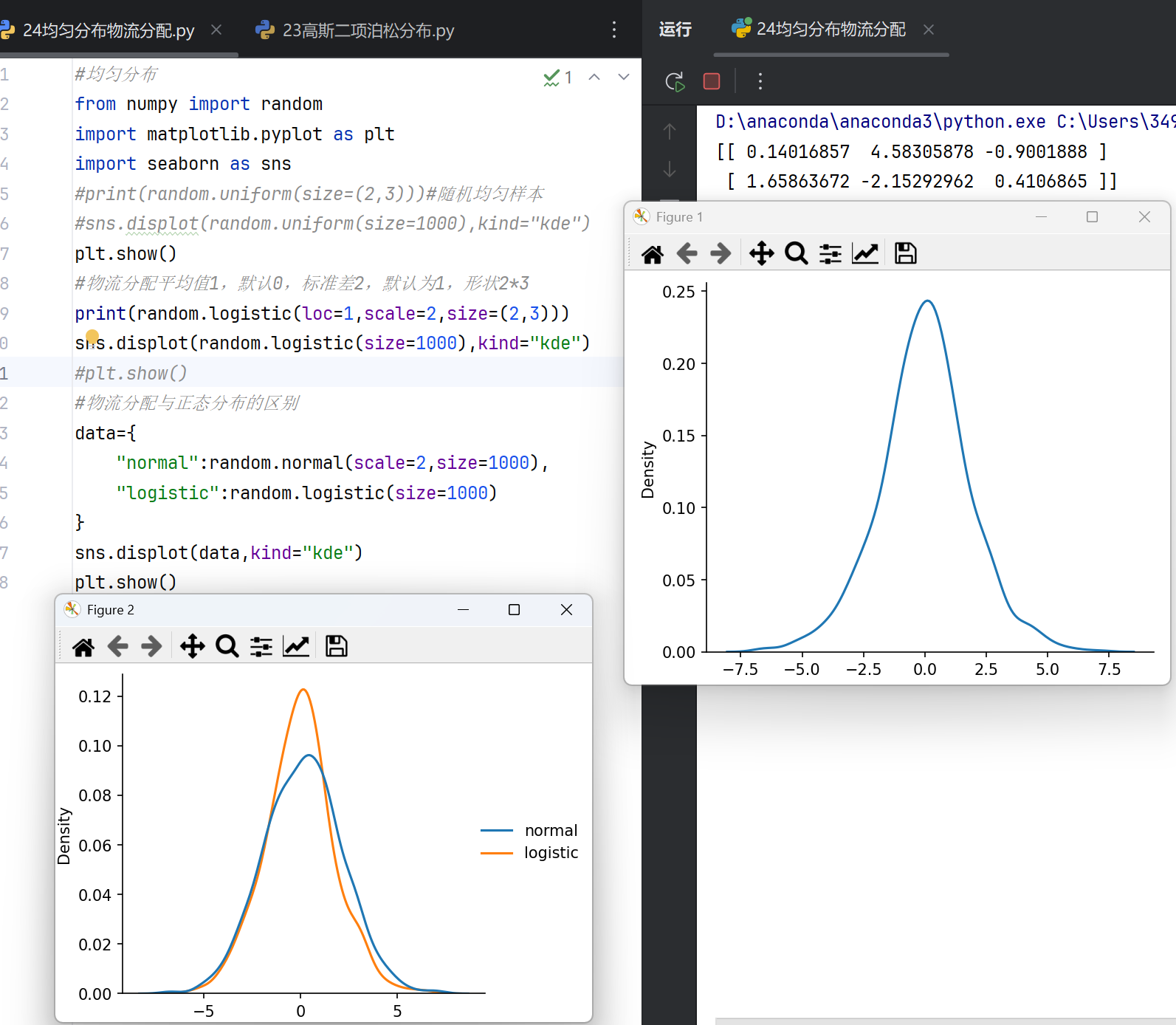
物流配送(逻辑斯蒂分布)
NumPy本身不直接提供物流配送的专用函数,但可通过数学和统计函数支持物流优化计算。常用功能包括:
距离计算:通过numpy.linalg.norm计算两点间的欧氏距离,或结合数组运算实现路径距离矩阵。
随机生成配送点坐标:使用均匀分布函数(如numpy.random.uniform)模拟客户或仓库的地理位置分布。
优化算法辅助:利用numpy.min、numpy.argmin等函数寻找最短路径或最优分配方案。
统计分析:通过numpy.mean、numpy.std等分析配送时间的分布特征。
5.多项式、指数和卡方分布
多项式分布
多项式分布(Multinomial Distribution)用于描述多类别独立试验的概率分布,例如掷骰子或多次分类抽样。在numpy中,相关功能主要通过random.multinomial实现,其核心参数包括试验次数n和各类别概率pvals。该函数返回每个类别出现的次数,结果形状与pvals一致。多项式分布是二项分布的推广,适用于离散型多变量场景。

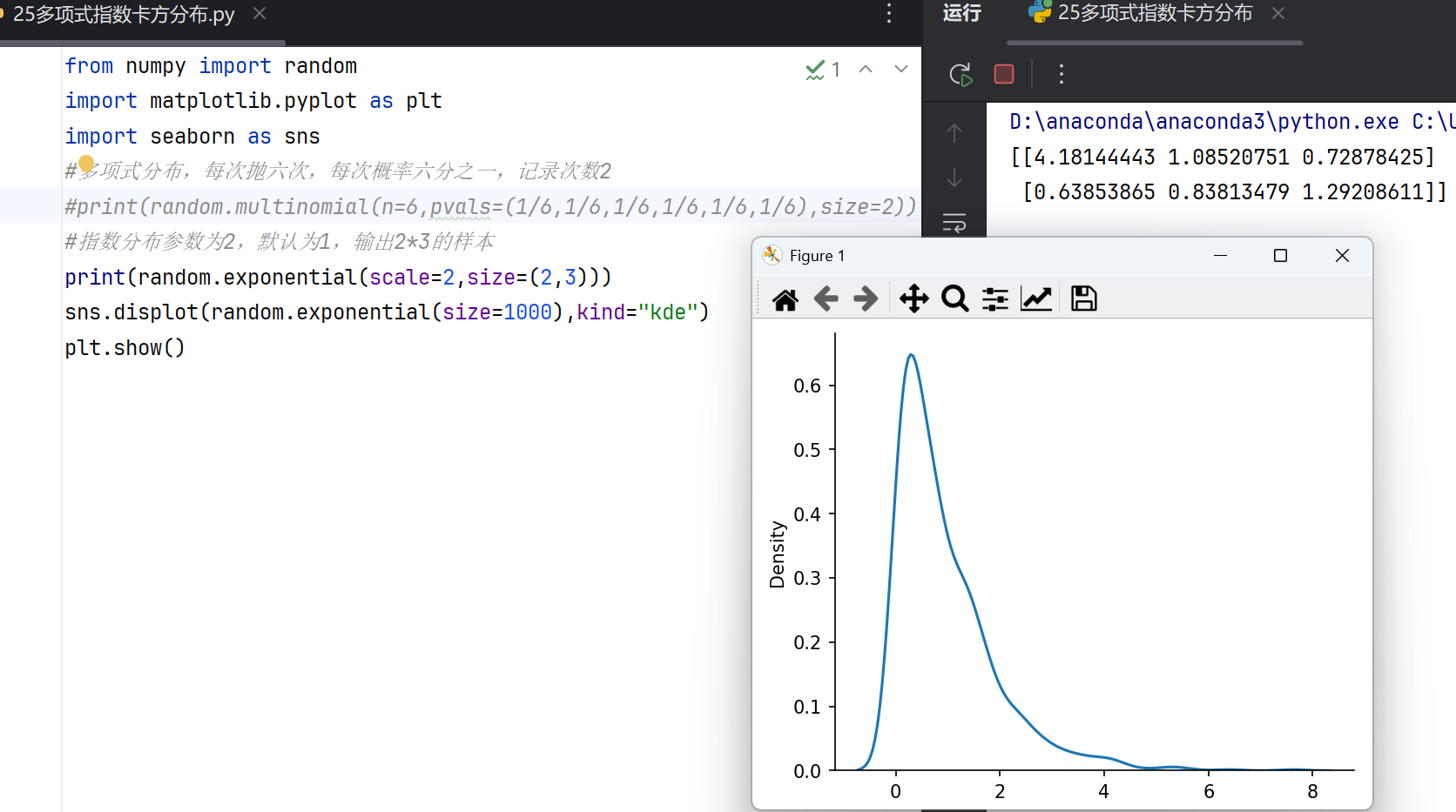
指数分布
指数分布(Exponential Distribution)常用于描述时间间隔的随机模型,如事件发生的等待时间。numpy通过random.exponential生成符合指数分布的随机数,关键参数为scale(即1/λ,λ为率参数)。该分布具有无记忆性,概率密度函数为:
函数支持指定输出数组形状,适用于模拟泊松过程或生存分析。
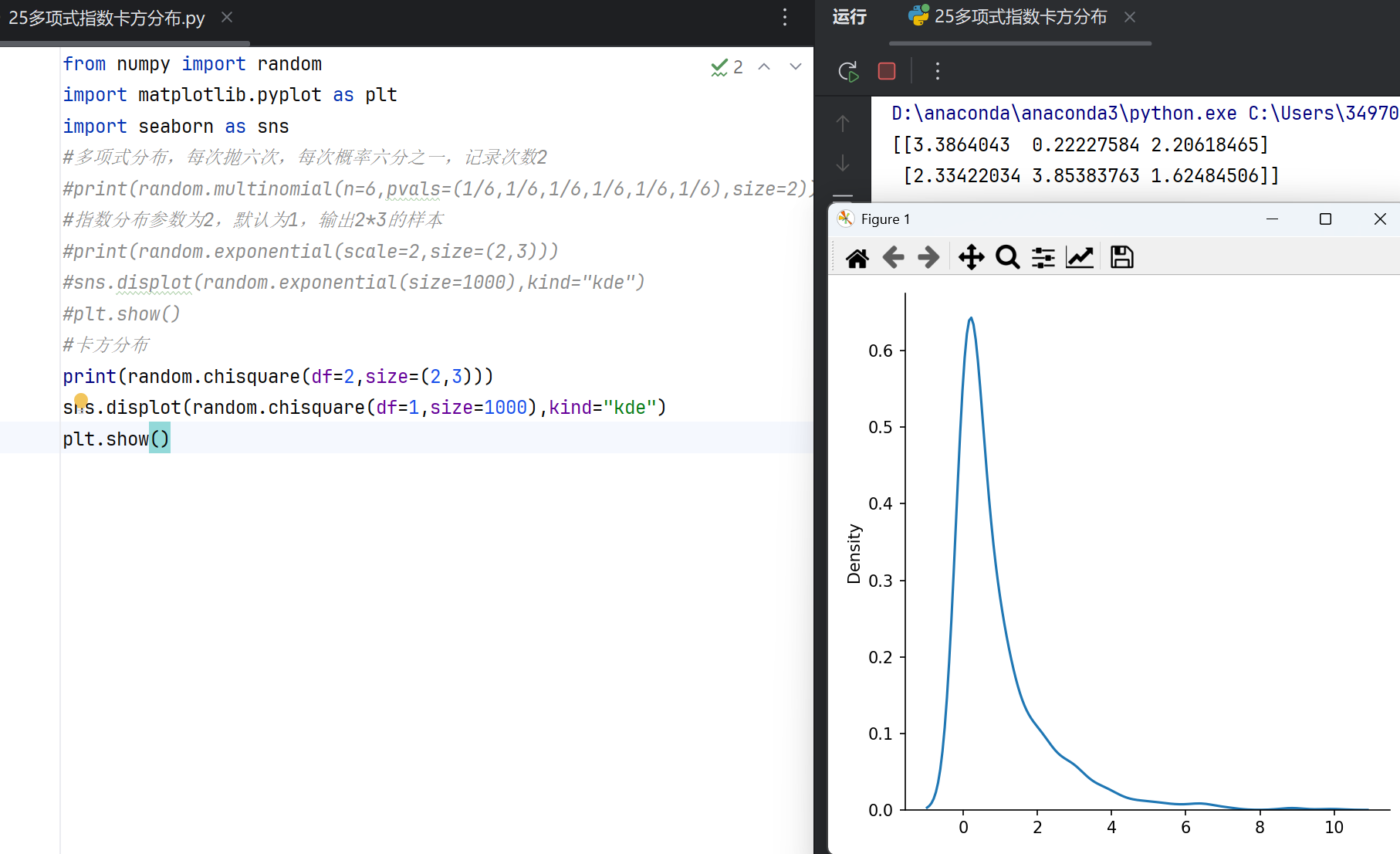
卡方分布
卡方分布(Chi-square Distribution)主要用于假设检验和方差分析,其随机变量是独立标准正态变量的平方和。numpy提供random.chisquare生成卡方分布样本,参数df代表自由度。概率密度函数为:
其中k为自由度。卡方分布常用于拟合优度检验或独立性检验,函数支持批量生成样本。
6.Rayleigh、帕累托和Zipf分布
Rayleigh分布(瑞丽分布)
Rayleigh分布常用于描述非负随机变量的幅度,例如信号处理中的振幅或风速分布。在numpy.random模块中,rayleigh(scale, size)函数用于生成Rayleigh分布的随机数:
- 参数:
scale(比例参数,默认1.0)控制分布的宽度;size指定输出形状。 - 特性:概率密度函数(PDF)为
,其中
为
scale参数。
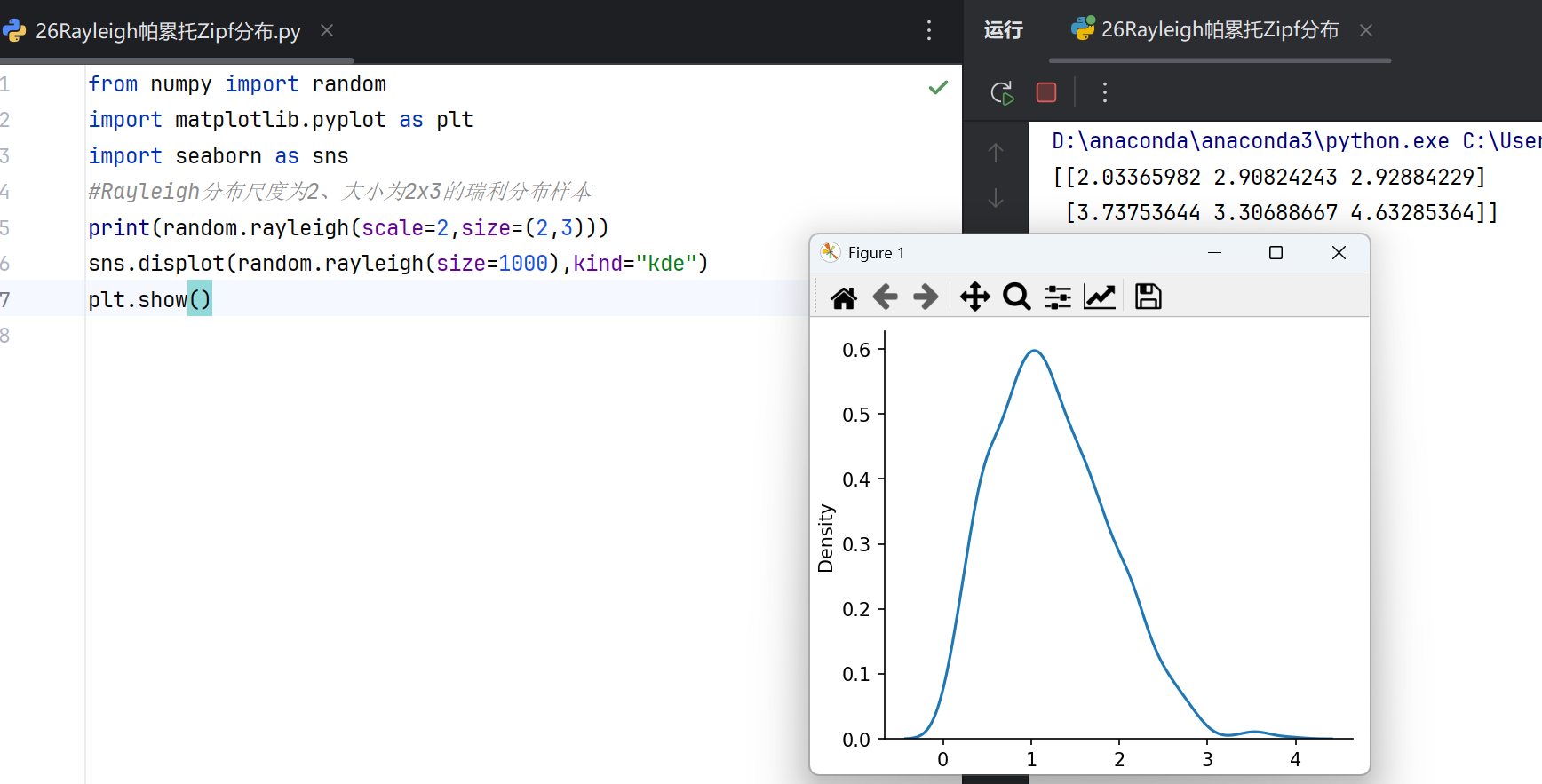
Rayleigh分布是一种连续概率分布,常用于描述非负随机变量的幅度,特别是当两个正交分量服从独立同分布的正态分布时,其合向量的模服从Rayleigh分布。典型应用包括信号处理中的幅度分析、风速建模和雷达散射截面建模。其概率密度函数(PDF)呈单峰形状,峰值位置由尺度参数决定,右尾衰减速度较慢。
帕累托分布
帕累托分布(Pareto)常用于描述“长尾”现象,如财富分布或网络流量。numpy.random模块的pareto(a, size)函数生成帕累托分布的随机数:
- 参数:
a为形状参数(又称尾指数),值越小尾部越厚;size为输出形状。 - 特性:PDF为
,其中
为最小尺度(numpy中固定为1)。
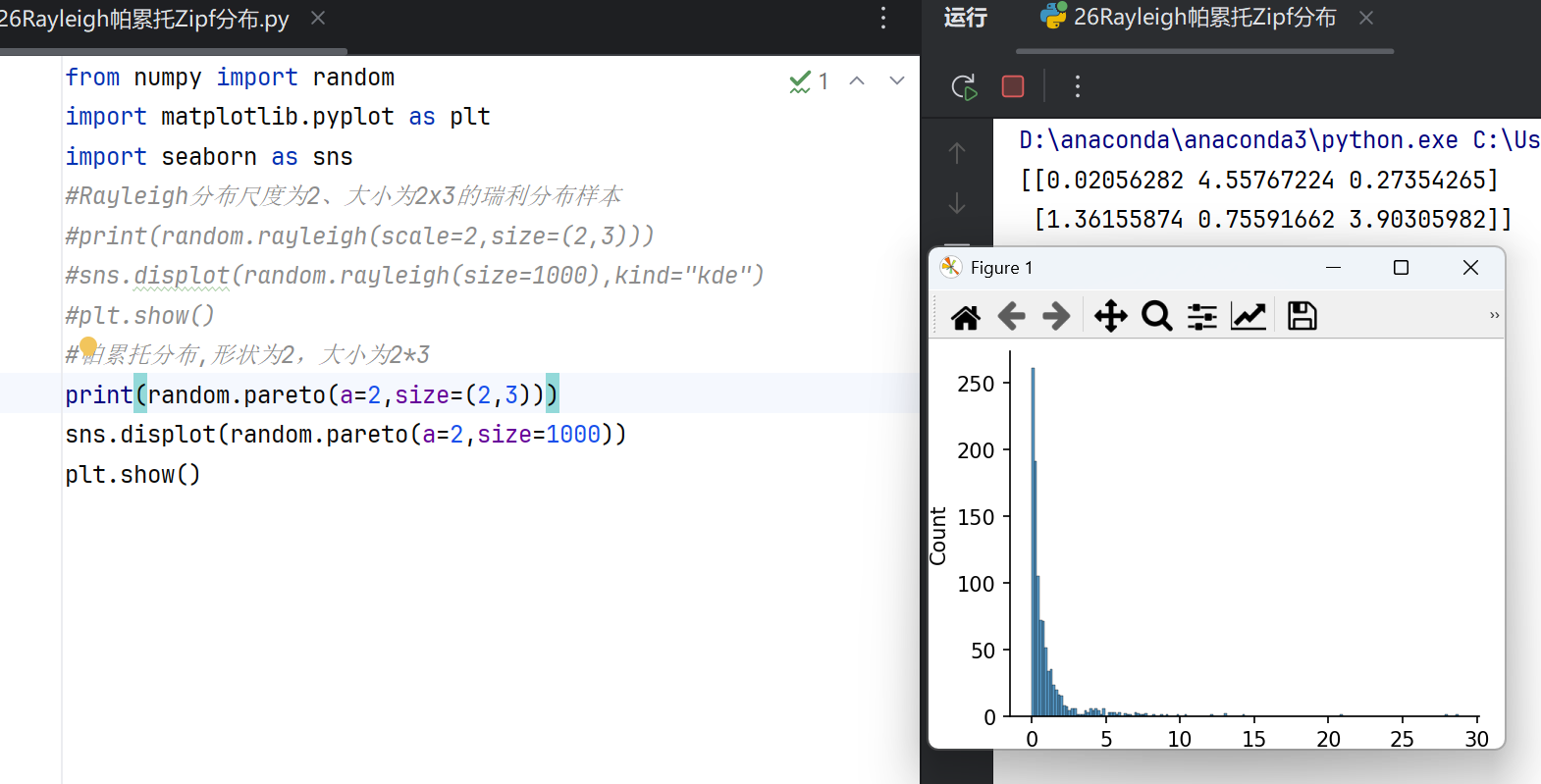
帕累托分布是一种幂律分布,描述“长尾”现象,即少数事件占据主要影响的情况。广泛应用于经济学(如财富分配)、网络流量分析(如文件大小分布)和自然灾害建模。其核心特征是尺度参数(最小值阈值)和形状参数(决定尾部厚度)。形状参数越小,尾部越厚,极端事件概率越高。
Zipf分布(齐夫分布)
Zipf分布用于模拟“幂律”现象,如自然语言中的词频分布。numpy.random模块的zipf(a, size)函数生成Zipf分布的随机整数:
- 参数:
a为幂律指数(大于1),值越小分布越倾斜;size为输出形状。 - 特性:概率质量函数(PMF)为
,其中
为排名(正整数)。
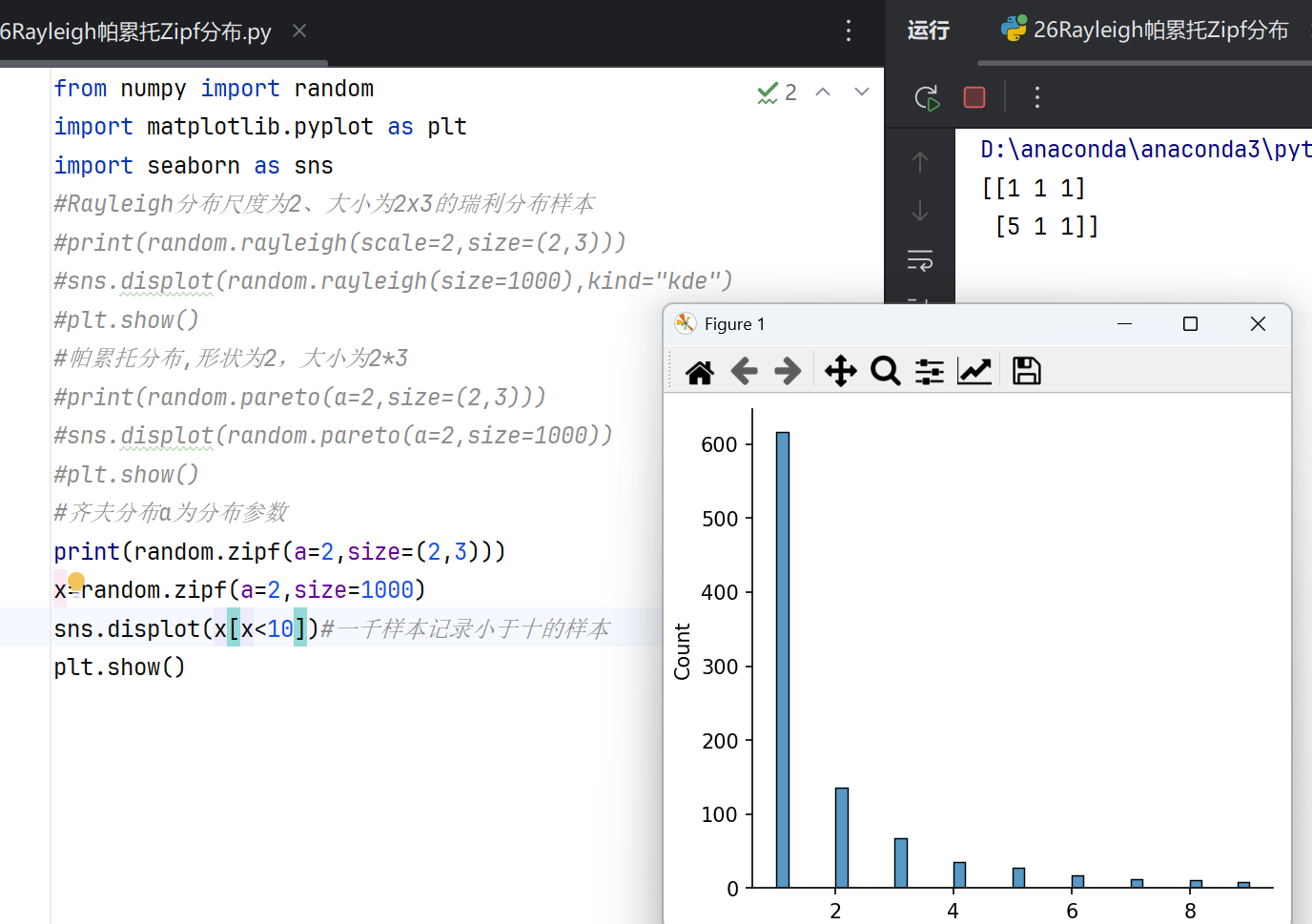
Zipf分布是一种离散概率分布,描述“排名-频率”关系,即第k个常见事件的频率与1/k^s成正比,其中s为分布参数。典型例子包括自然语言中单词的使用频率、城市人口排名等。当s=1时,严格满足Zipf定律;s越大,高频事件占比越高,分布越陡峭。该分布常用于语言学、信息检索和网络科学。
以上函数均基于逆变换采样实现,可通过调整参数控制分布形态。
三、通用公式ufunc的使用
1.创建ufunc函数入门
ufunc简介
通用函数(Universal Function,简称ufunc)是NumPy中一种特殊的函数,能够对数组中的每个元素执行快速的逐元素操作。ufunc支持广播机制,能够处理不同形状的数组,并自动调整输入数组的形状以完成计算。ufunc还支持多种方法,如reduce、accumulate和reduceat,适用于聚合和累积操作。
ufunc分为一元和二元两种类型:
- 一元ufunc:接收一个输入数组,如平方根、绝对值等函数。
- 二元ufunc:接收两个输入数组,如加法、乘法等函数。
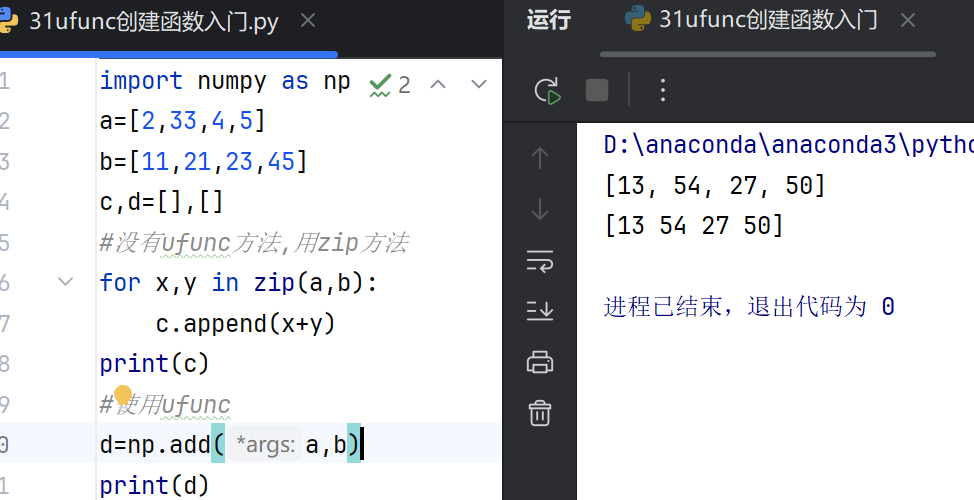
创建ufunc入门:创建自定义的ufunc通常可以通过NumPy的frompyfunc或vectorize函数实现。虽然以下内容不涉及具体代码,但可以了解其基本逻辑。
使用frompyfunc创建:frompyfunc将普通的Python函数转换为ufunc。需要指定输入参数的数量和输出参数的数量。生成的ufunc可以处理数组的逐元素操作,但返回类型为Python对象,可能影响性能。
使用vectorize创建:vectorize是另一种创建ufunc的方法,相比frompyfunc更加灵活。可以指定输出类型以提高性能,并支持广播机制。适合将标量函数转换为数组操作。
注意事项
- 自定义ufunc的性能可能不如内置的ufunc,尤其在处理大型数组时。
- 确保输入函数能够正确处理标量值,因为ufunc会对每个元素调用该函数。
- 考虑使用NumPy内置的ufunc组合实现功能,避免不必要的自定义。
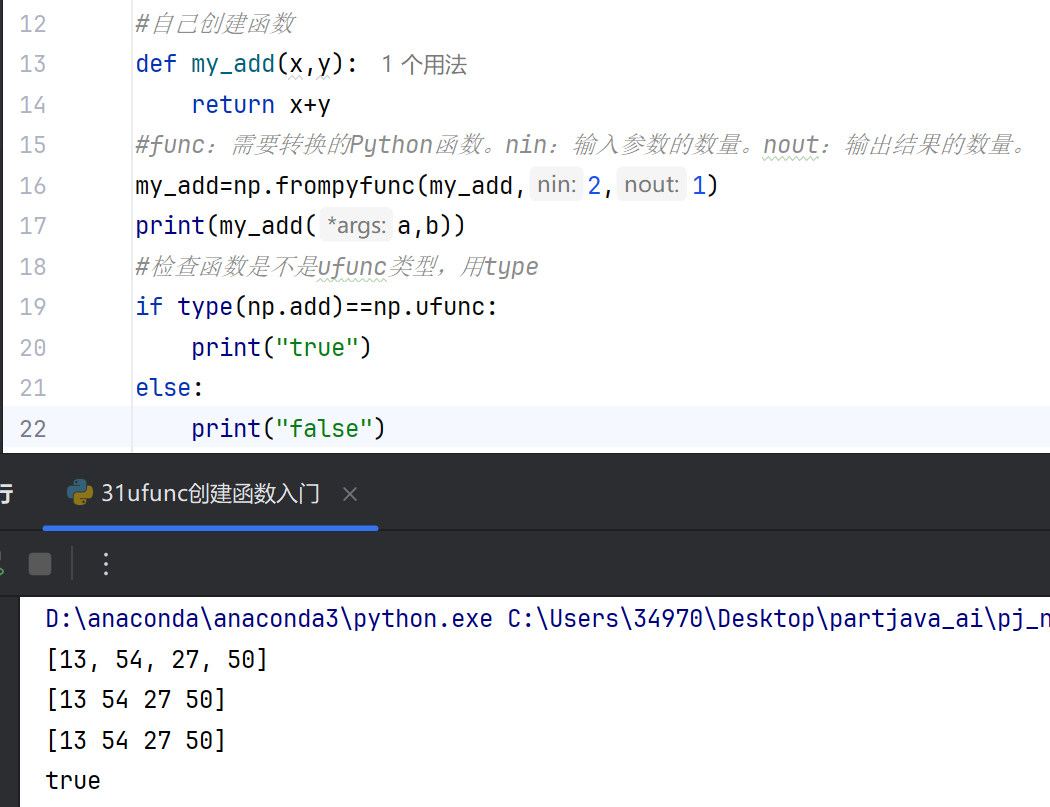
通过以上方法,可以扩展NumPy的功能,满足特定的计算需求。
2.简单算数和四舍五入
简单算术运算
NumPy 提供了多种基础算术运算函数,能够高效处理数组之间的数学操作。这些函数支持广播机制,可以对不同形状的数组进行计算。
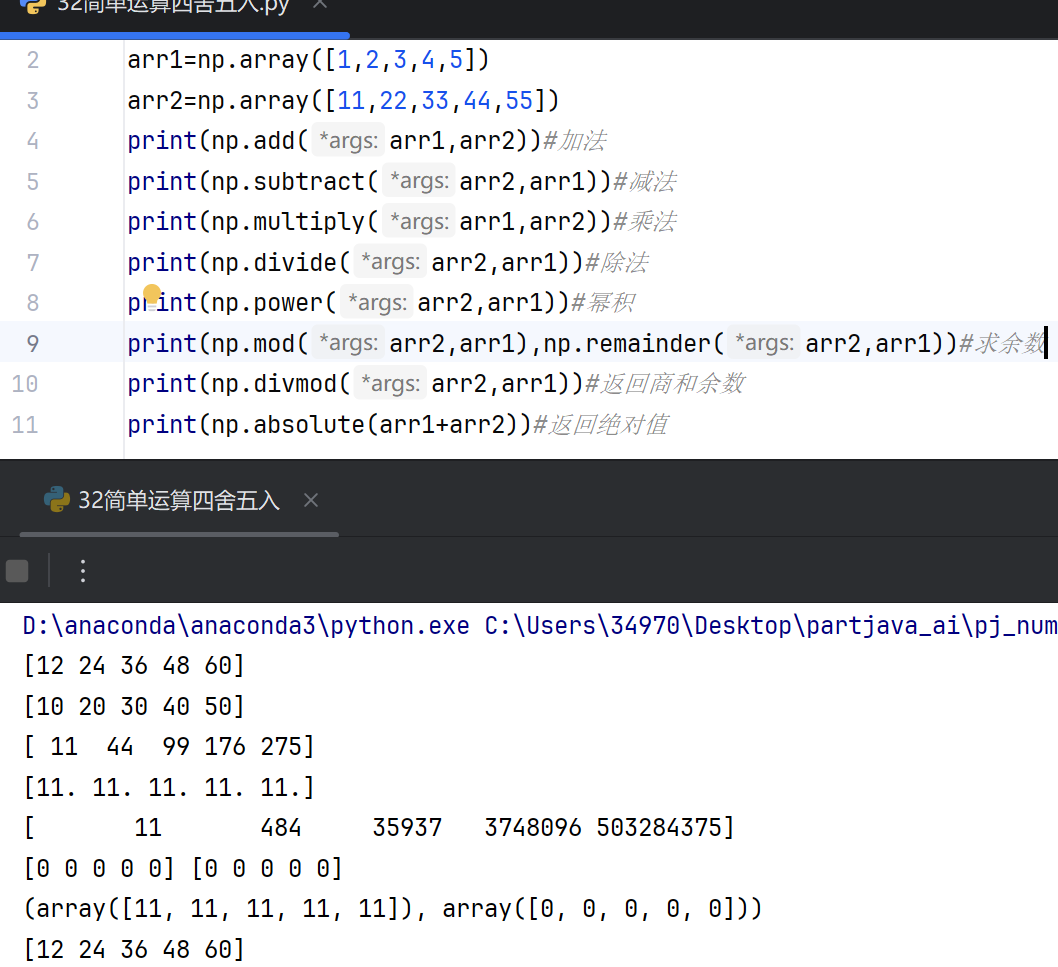
加法:np.add() 函数用于对两个数组进行逐元素相加,或者将标量值与数组中的每个元素相加。
减法:np.subtract() 函数用于计算两个数组之间的逐元素差值,或者从数组中减去一个标量值。
乘法:np.multiply() 函数用于执行逐元素乘法,支持数组与标量或另一个数组相乘。
除法:np.divide() 函数用于对数组进行逐元素除法运算,支持整数和浮点数除法。
幂运算:np.power() 函数用于计算数组元素的幂次,例如将一个数组的每个元素提升到另一个数组对应元素的幂次。
取模:np.mod() 函数返回除法运算后的余数,适用于整数和浮点数运算。
四舍五入
NumPy 提供了多种四舍五入相关的函数,用于控制数值的精度和舍入方式。
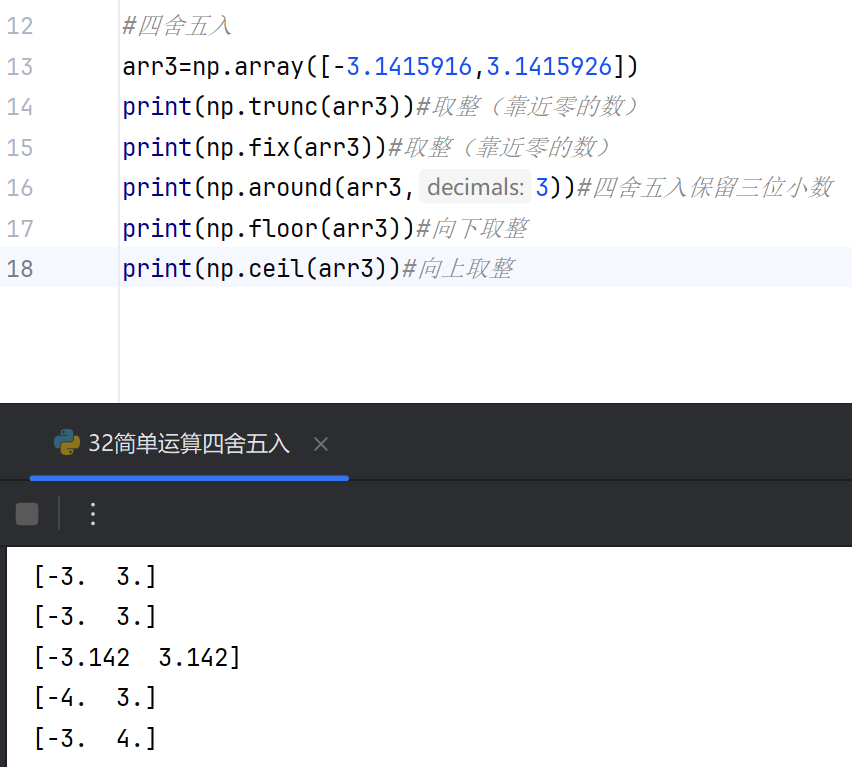
四舍五入:np.round() 函数将数组中的每个元素四舍五入到指定的小数位数。默认小数位数为 0,即舍入到最接近的整数。
向下取整:np.floor() 函数将数组中的每个元素向下取整,返回不大于该元素的最大整数。
向上取整:np.ceil() 函数将数组中的每个元素向上取整,返回不小于该元素的最小整数。
截断取整:np.trunc() 函数将数组中的每个元素向零方向截断,直接去掉小数部分。
这些函数在数据处理和科学计算中广泛应用,能够帮助用户快速实现数值的精确控制。
3.对数、求和、乘积
对数
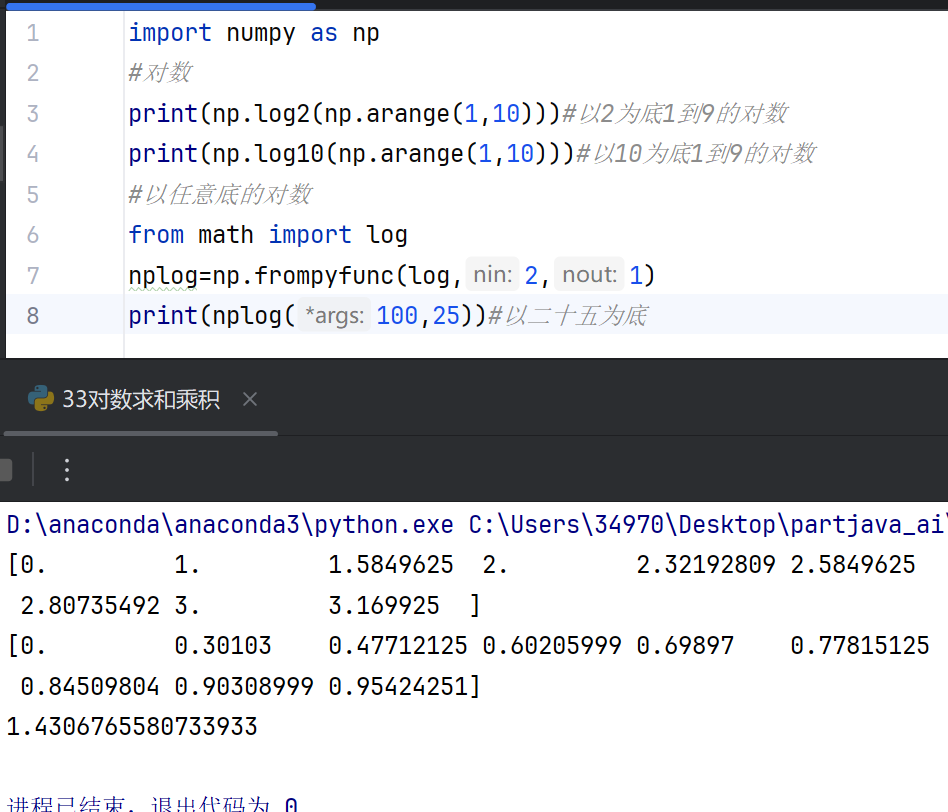
NumPy提供多种对数函数用于数值计算,包括自然对数、以2为底的对数以及以10为底的对数。这些函数能够逐个元素地对数组进行操作,返回相同形状的数组。
- 自然对数(log):计算数组元素的自然对数,即以e为底的对数。
- 以2为底的对数(log2):计算数组元素以2为底的对数。
- 以10为底的对数(log10):计算数组元素以10为底的对数。
- 对数函数(log1p):计算数组中每个元素加1后的自然对数,适用于数值极小的情况,提高精度。
求和
NumPy的求和函数可以对数组进行不同维度的求和操作,支持对整个数组或沿着指定轴进行求和。
- 数组总和(sum):计算数组所有元素的总和。
- 沿轴求和(sum with axis):指定轴参数后,函数会沿着该轴进行求和,返回降维后的数组。
- 累积求和(cumsum):返回数组元素的累积和,支持沿指定轴计算部分累积和。

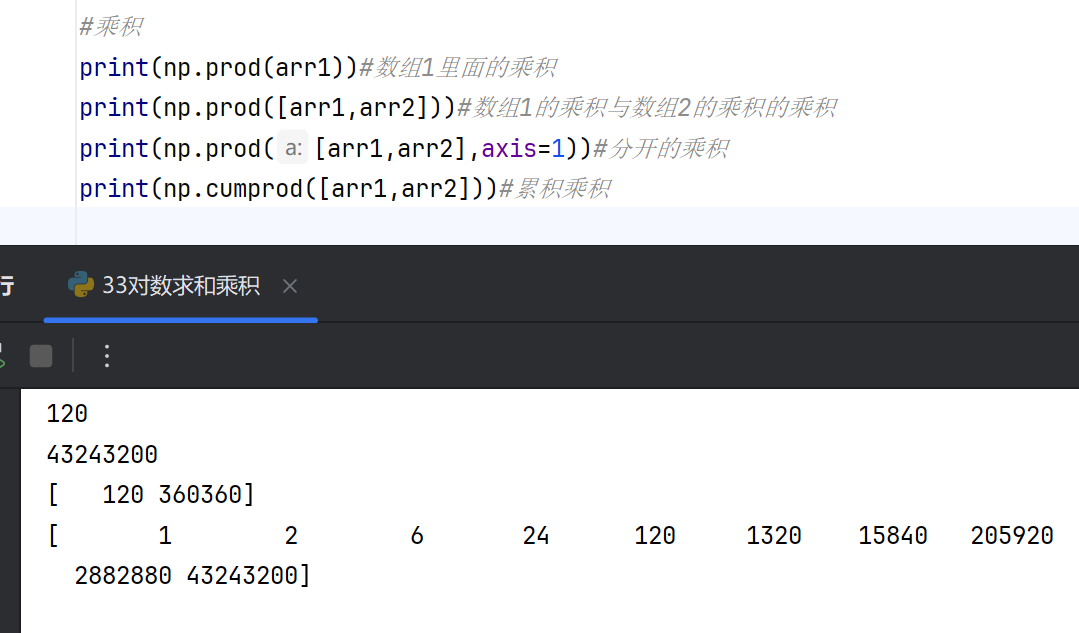
乘积
NumPy的乘积函数用于计算数组元素的乘积,支持对整个数组或沿指定轴进行乘积操作。
- 数组总乘积(prod):计算数组所有元素的乘积。
- 沿轴乘积(prod with axis):指定轴参数后,函数会沿着该轴进行乘积计算,返回降维后的数组。
- 累积乘积(cumprod):返回数组元素的累积乘积,支持沿指定轴计算部分累积乘积。
4.差异、最大公约数和最小公倍数
差异(Difference)
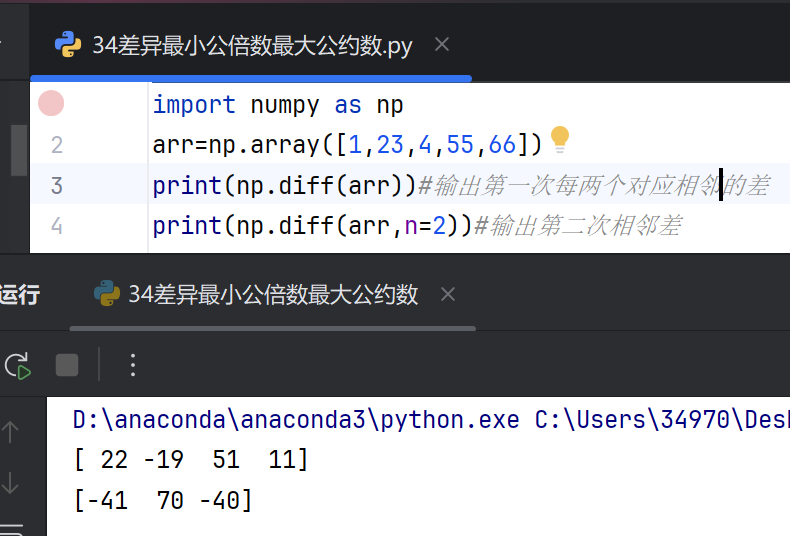
在NumPy中,差异通常指的是计算数组中相邻元素之间的差值。numpy.diff()函数用于实现这一功能,它会返回一个由相邻元素差值构成的新数组。例如,给定一个数组[a, b, c],numpy.diff()会返回[b - a, c - b]。该函数可以多次递归调用以计算更高阶的差分(如二阶差分)。
numpy.diff()的主要参数包括:
a:输入的数组。n:差分的阶数,默认为1。axis:沿指定轴计算差分。
最大公约数(Greatest Common Divisor, GCD)
NumPy提供了numpy.gcd()函数来计算两个或多个整数的最大公约数(GCD)。最大公约数是能够整除所有输入整数的最大正整数。例如,12和15的GCD是3。
numpy.gcd()的主要特点:
- 支持广播机制,可以处理数组输入。
- 输入可以是标量或数组。
- 如果输入包含负数,函数会取其绝对值进行计算。

最小公倍数(Least Common Multiple, LCM)
numpy.lcm()函数用于计算两个或多个整数的最小公倍数(LCM)。最小公倍数是能够被所有输入整数整除的最小正整数。例如,4和6的LCM是12。
numpy.lcm()的主要特点:
- 支持广播机制,可以处理数组输入。
- 输入可以是标量或数组。
- 如果输入包含负数,函数会取其绝对值进行计算。

关系与用途
numpy.diff()常用于信号处理、时间序列分析等领域,用于检测数据的变化趋势。numpy.gcd()和numpy.lcm()在数学运算、密码学或需要处理整数关系的场景中非常有用。- GCD和LCM通常一起使用,例如在分数运算或周期计算中。
5.三角函数和双曲函数
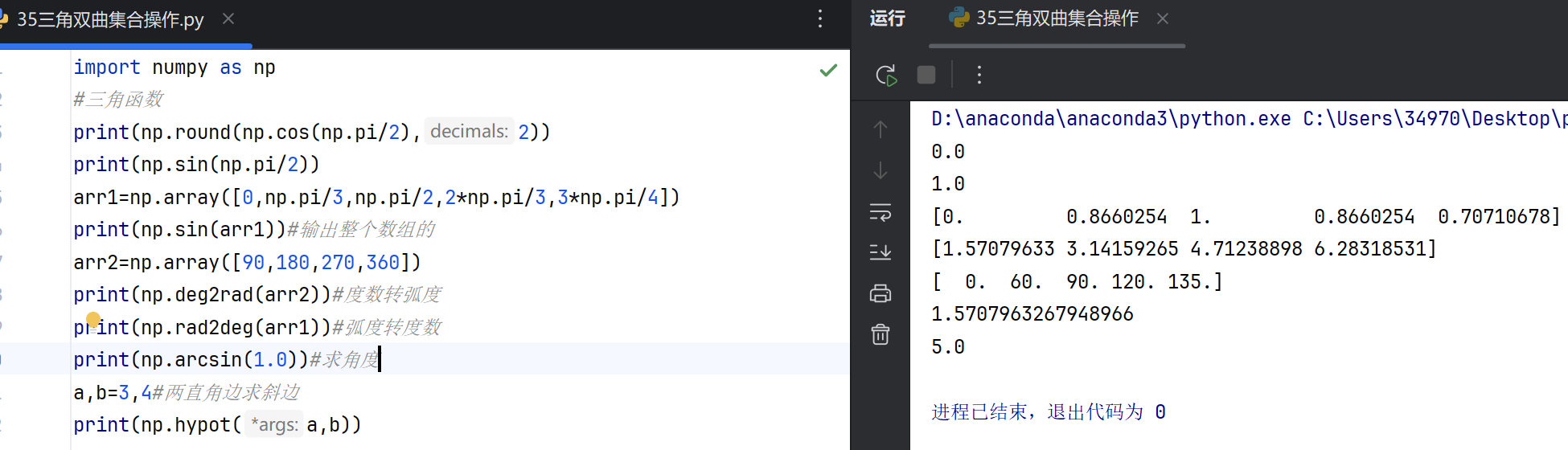
三角函数
NumPy提供了标准的三角函数,输入单位为弧度(radians),支持数组运算:
sin(x):计算正弦值。cos(x):计算余弦值。tan(x):计算正切值。arcsin(x):计算反正弦值,返回值范围在[-π/2, π/2]。arccos(x):计算反余弦值,返回值范围在[0, π]。arctan(x):计算反正切值,返回值范围在[-π/2, π/2]。arctan2(y, x):计算从x轴到点(x, y)的夹角(考虑象限),返回值范围在[-π, π]。degrees(x):将弧度转换为角度。radians(x):将角度转换为弧度。
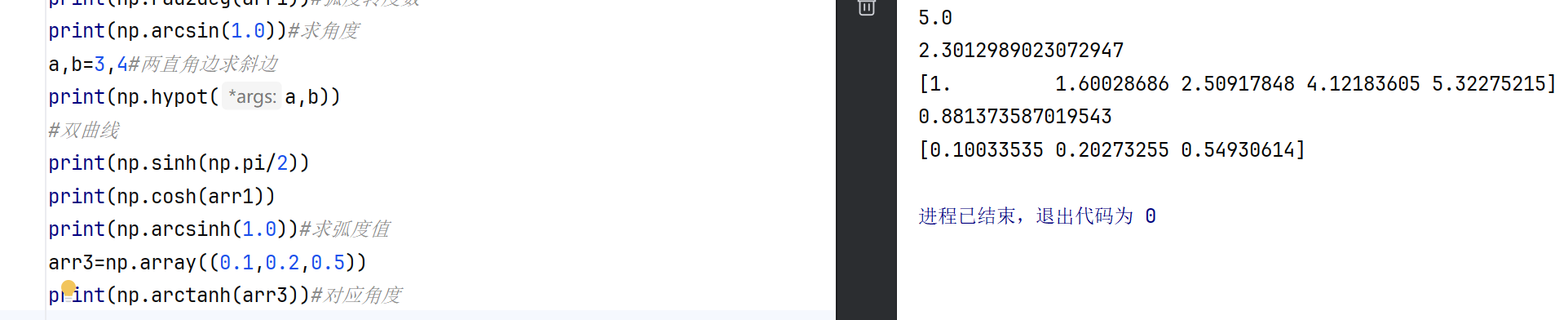
双曲函数
双曲函数基于指数函数定义,支持数组输入:
sinh(x):计算双曲正弦值。cosh(x):计算双曲余弦值。tanh(x):计算双曲正切值。arcsinh(x):计算反双曲正弦值。arccosh(x):计算反双曲余弦值(输入需≥1)。arctanh(x):计算反双曲正切值(输入需在(-1, 1)范围内)。
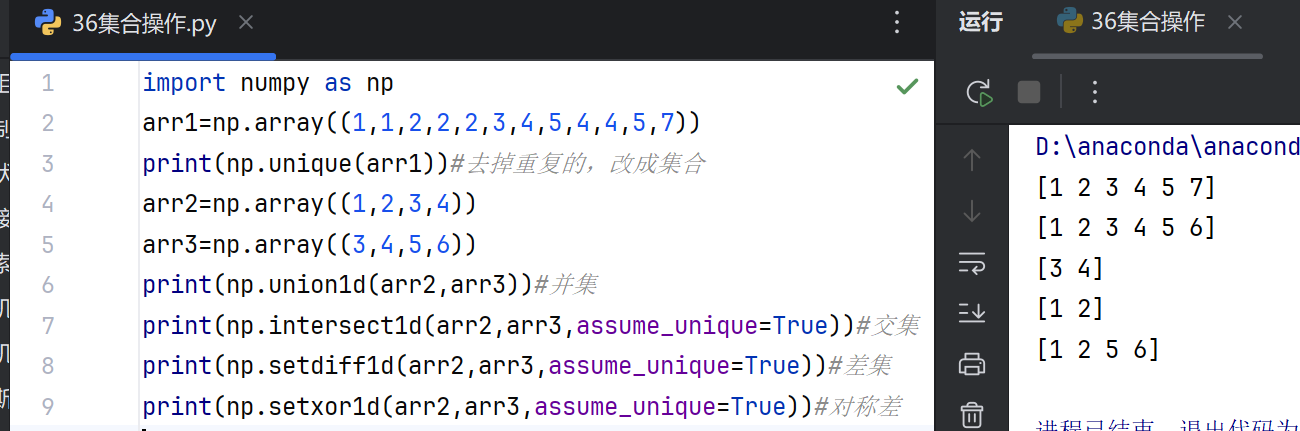
6.集合操作
NumPy提供针对一维数组的集合运算,类似数学中的集合操作:
unique(x):返回数组的唯一值并排序。intersect1d(x, y):返回两个数组的交集并排序。union1d(x, y):返回两个数组的并集并排序。setdiff1d(x, y):返回在x中但不在y中的元素(差集)。setxor1d(x, y):返回仅出现在x或y中(非交集)的元素。in1d(x, y):检查x的元素是否存在于y中,返回布尔数组。
这些函数均支持对数组的高效操作,适用于数值计算和数据分析场景。





















 666
666

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








