八皇后 Checker Challenge

        这里不对DFS和BFS作介绍了，只对这道题作分析。

朴素思路就是把所有情况都枚举一遍，但强行枚举的话一共有种可能，这时候就要用搜索+递归来解决了。

简单构思一下就会想到，我们先把第一列的棋子下去，然后再到第二行去找哪一块可以下棋（横纵和对角线上都没有棋子），以此类推，再通过递归把棋子换位置下来寻找其他答案。

那么现在的问题就是怎么构造搜索递归和怎么确定某一个空位是否能下棋子。根据题目要求的输出方法我们以列数为DFS参数（按字典序输出），然后再用两个数组来表示横和纵向是否有棋子。

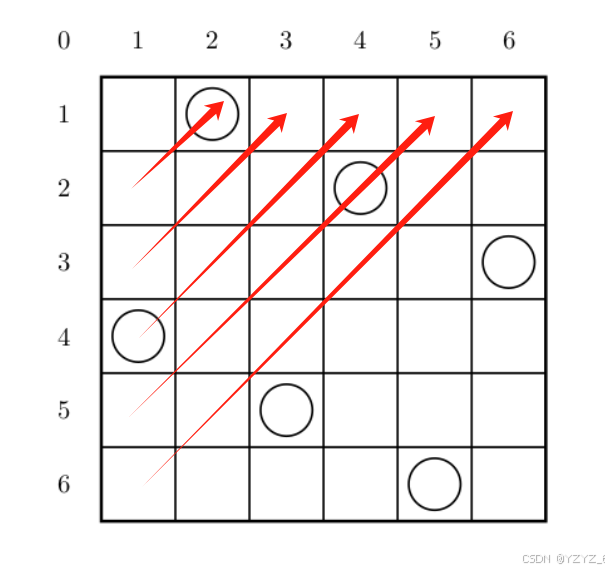
我们来观察对角线上格子的特点，(1,2),(2,1) ; (1,3),(2,2),(3,1) 可以发现，同一个对角线上横坐标和纵坐标的和是一致的，我们可以构造一个数组 a[ i + j ] ，来表示这个方向的对角线上是否有棋子。

再来看这个方向对角线格子的特点，(1,1),(2,2),(3,3),(4,4)不难发现，同一个对角线上横坐标和纵坐标的差值是一样的，我们可以构造一个数组a[ i - j + n ]，来表示这个方向对角线是否有棋子，但是 i-j 有可能是负数，所以我们还需要加上一个n。至此这道题思路已经构造完成了。

这里贴上洛谷上大佬的题解

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
int a[100],b[100],c[100],d[100];
//a数组表示的是行；
//b数组表示的是列；
//c表示的是左下到右上的对角线；
//d表示的是左上到右下的对角线；
int total;//总数:记录解的总数
int n;//输入的数，即N*N的格子，全局变量，搜索中要用
int print()
{
    if(total<=2)//保证只输出前三个解，如果解超出三个就不再输出，但后面的total还需要继续叠加
    {
        for(int k=1;k<=n;k++)
        cout<<a[k]<<" ";//for语句输出
        cout<<endl;
    }
    total++;//total既是总数，也是前三个排列的判断
}
void queen(int i)//搜索与回溯主体
{
    if(i>n)
    {
        print();//输出函数，自己写的
        return;
    }
    else
    {
        for(int j=1;j<=n;j++)//尝试可能的位置
        {
            if((!b[j])&&(!c[i+j])&&(!d[i-j+n]))//如果没有皇后占领，执行以下程序
            {
                a[i]=j;//标记i排是第j个
                b[j]=1;//宣布占领纵列
                c[i+j]=1;
                d[i-j+n]=1;
                //宣布占领两条对角线
                queen(i+1);//进一步搜索，下一个皇后
                b[j]=0;
                c[i+j]=0;
                d[i-j+n]=0;
                //（回到上一步）清除标记
            }
        }
    }
}
int main()
{    
    cin>>n;//输入N*N网格，n已在全局中定义
    queen(1);//第一个皇后
    cout<<total;//输出可能的总数
    return 0;
}