新型可逆组合电路设计

一种用于低功耗计算的新型可逆组合电路设计

摘要

随着纳米级设计技术的进步，电路中经常出现瞬态故障，因此需要低功耗设计。近年来，可逆逻辑已成为低功耗电路设计领域的一个新兴研究热点。其应用领域包括 CMOS低功耗设计、量子计算、网络安全、数字信号与图像处理、光电子和纳米技术。本文对各种可逆全加器和可逆全减器门及其量子代价值在实现节能型逻辑设计方面的有效性进行了比较研究。文中讨论了一种利用现有可逆逻辑门和新改进的可逆逻辑门实现可逆组合电路的新设计方法。可逆逻辑电路采用Verilog代码进行设计和实现，仿真结果通过 Xilinx ISE 9.2i版本获得。

关键词 -可逆逻辑门，低功耗，全加器，全减器，量子代价，垃圾输出，Verilog代码。

一、引言

根据摩尔定律，目前芯片上的半导体器件密度允许在纳米级的芯片上集成数百万个晶体管。因此，器件密度不断增加，同时器件尺寸和器件电压也在缩小。当前制造的器件采用了纳米技术。此类应用的一个主要限制是硬件实时运行时对电池/太阳能电源的基本需求。为了降低功耗并提高能效，研究人员已采用基于MEMS开关[4],碳纳米管[3],和可逆逻辑[5]的技术。可逆逻辑在实时系统中具有广泛的应用。与传统（不可逆逻辑）相比，可逆逻辑产生的热量更少，能够检测信息丢失问题，并实现零功耗。因此，可逆逻辑在高速低功耗VLSI芯片中需求更高。

逻辑可逆计算意味着关于计算状态没有信息丢失，因此我们可以通过计算恢复任何早期阶段反向计算或撤销结果。而物理可逆性是指不产生热能损耗的过程。计算系统仅在比特传输从零到一发生时才会耗散热能，这与电压电平从正变为负相同。可逆电路将直接把电荷从一个节点移动到下一个节点，而不是将电压改变为新的电平，而这种变化所需的能量会以热能形式释放。因此，在每次转换中预期的能量损耗非常少。但完全的物理可逆性在实际中是无法实现的。

本文阐述了一种基于可逆逻辑概念的数字加法器和减法器电路设计及其功能的新型方法。此外，对各类可逆逻辑门设计的量子代价值和垃圾输出数量进行了比较。总体而言，本文在一定程度上探讨了低功耗设计问题。

本文其余部分组织如下：第二节聚焦于相关文献综述。第三节介绍可逆逻辑，并讨论用于构建基于可逆逻辑电路的高效逻辑模块的现有设计。第四节提出利用多种可逆逻辑电路的组合电路设计。第五节展示所提方法的仿真结果及其性能比较。第六节对本文进行总结。

II. 文献综述

使用可逆门实现可编程逻辑是一个正在发展的研究领域。可逆逻辑电路在设计未来计算机的低功耗数字电路方面具有重要意义。因此，许多研究人员受到启发，采用可逆逻辑方法来制造先进计算电路、低功耗 CMOS设计电路等。1960年，朗道尔[1]的研究结果表明，在不可逆逻辑中，当在绝对温度T下进行计算时，每丢失一位信息就会耗散k T ln2焦耳的热能。在室温下，每位信息耗散的热能为2.9×10-21 J。此外，1973年，研究人员本内特[2],发现，在使用可逆逻辑设计的电路中，kTln2焦耳的能量耗散可以在很大程度上被最小化。

文献中报道的可逆门的详细列表在[8]中进行了讨论。其中一些突出的门包括费曼门[9], 、托佛利门[10], 、弗雷德金门[7], 、克恩托普夫门[8]以及马戈卢斯门[11]。实现可逆逻辑最常用的技术包括电荷恢复逻辑（CRL） [12], 、分层CRL[13], 、可逆能量恢复逻辑（RERL） [14],[15],和NMOS RERL（nRERL）[16]。此外， [17]和[18]介绍了可逆电路的光电和基于纳米米的实现。

论文[19]研究了时序可逆逻辑元件的构造。垃圾最小化一直是设计任何可逆电路时面临的最大挑战。垃圾输出被定义为为了使一个n输入k输出的布尔函数[（n, k） 函数]成为可逆[20]而增加的输出数量。

III. 可逆逻辑

可逆逻辑概念反映了输入和输出向量之间的一对一映射，即每个输入向量生成唯一的输出向量，反之亦然。唯一的可逆门是非门。更正式地说，一个可逆逻辑门表示为 N N ，即N输入和N输出。N N可逆门的表示法可以用 (1)和(2)分别表示输入和输出向量。

$$ Iv=(I1,I2,I3,I4,........................IN) \tag{1} $$

$$ Ov=(O1,O2,O3,......................ON) \tag{2} $$

基于可逆逻辑实现任何特定的布尔函数时，需要确保或优化某些设计约束。首先，在可逆逻辑电路中，输入和输出的数量必须相等。其次，每个输入模式必须对应唯一的输出模式。第三，不允许扇出，即每个输出只能使用一次。最后，所得到的电路必须是无环的。此外，可逆门/电路会产生一些未使用的输出，称为“垃圾输出”，应尽量减少这些垃圾输出。

IV. 可逆逻辑门的现有设计

A. 传统可逆逻辑门

1) 费曼门

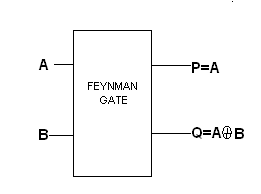
一个2*2费曼门[9]如图1所示，对于输入向量I(A, B)，其输出定义为P=A和Q=A xor B。费曼门的量子代价为1。费曼门（FG）也称为受控非门（controlled not gate）。

用途 ：用于所需输出的复制。可作为复制门使用。

2) Fredkin门

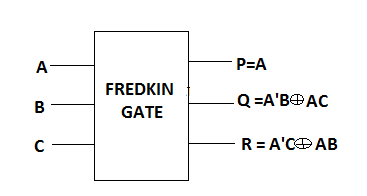
一个3*3弗雷德金门[7]如图2所示。对应于输入 I(A, B, C)，输出定义为P=A，Q=A′.B xor A.C 和 R=A′.C xor A.B，如图所示。弗雷德金门的量子代价是5。

用途 ：任何可逆电路都可以通过它来设计。

3) Peres门

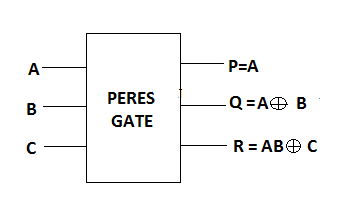
一个3*3佩雷斯门[10]如图3所示。对应于输入I(A, B, C)到该门，其输出定义为P=A，Q=A xor B，以及R= A.B xor C，如图所示。佩雷斯门的量子代价为4。

4) 托佛利门

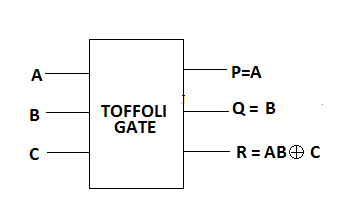
一个3*3托佛利门[11]如图4所示。对应于输入 I(A, B, C)，输出定义为P=A，Q=B和R=A.B xor C。托佛利门的量子代价为5。托佛利门也被称为通用可逆门。

5) NG门

图5显示了一个3*3新门(NG)。输入向量为I(A,B)，输出定义为P=A，Q=A.B xor C 和 R=A’.B’ xor C’。该NG门的量子代价为4。

B. 高级可逆逻辑门

1) DPG门

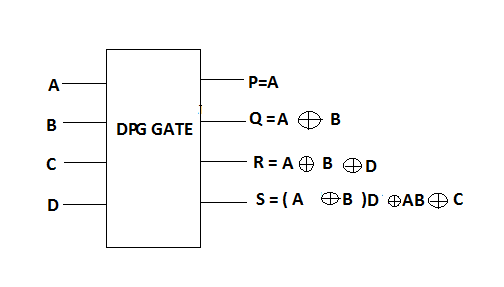
图6显示了一个4*4双Peres门(DPG)，其中对应于输入向量I(A,B,C,D)，输出定义为P=A，Q=A xor B， R=A xor B xor D 和 S=(A xor B).D xor (A.B xor C)。

用途 ：DPG门主要用于减少垃圾输出。

2) TSG门

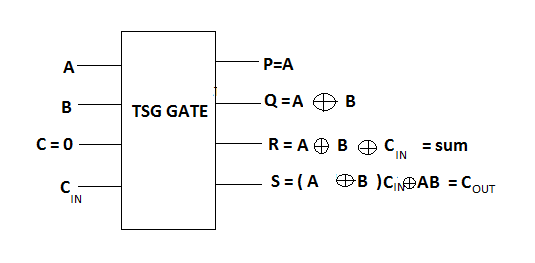
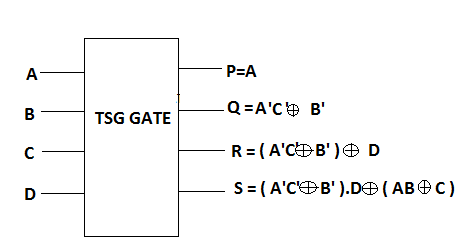
图7展示了一个4*4的TSG门，对于输入I(A, B,C, D)，其输出定义为P=A，Q=A’.C’ xor B’，R=(A’.C’ xor B’) xor D以及 S=(A’.C’ xor B’).D xor (A.B xor C)。

V. 基于可逆逻辑门的组合电路设计

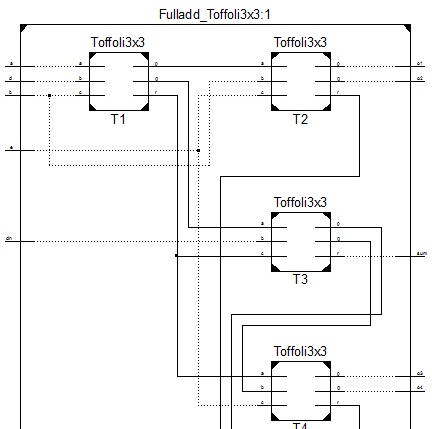
1) 基于托佛利门的全加器设计：

通过使用Toffoli可逆门，当D =1且E =0时，如图8所示，可以设计全加器。

2) 基于弗雷德金门的全加器设计：

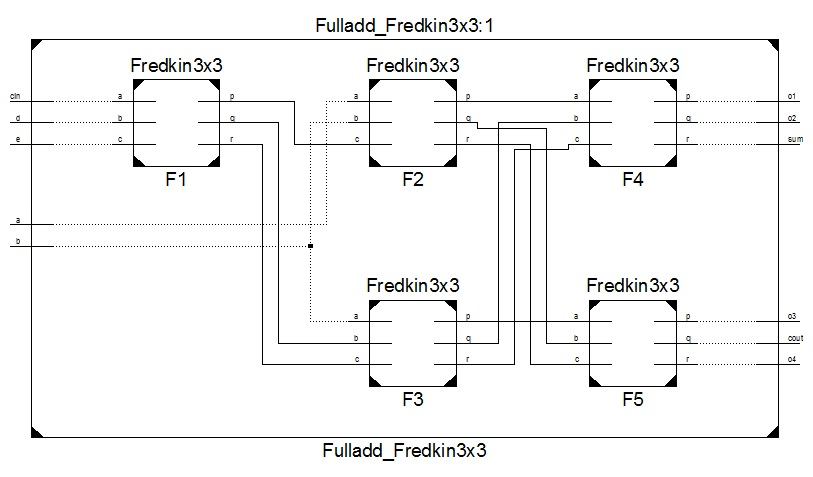
通过使用Fredkin门，当D=1、E=0时，如图9所示，可以设计全加器。

3) 使用DPG门的全加器设计：

当输入C=0如图10所示时，可使用单个DPG门构建可逆全加器电路。

4) 使用TSG门的全加器设计：

当输入C=0如图11所示时，可使用单个TSG门构建可逆全加器电路。

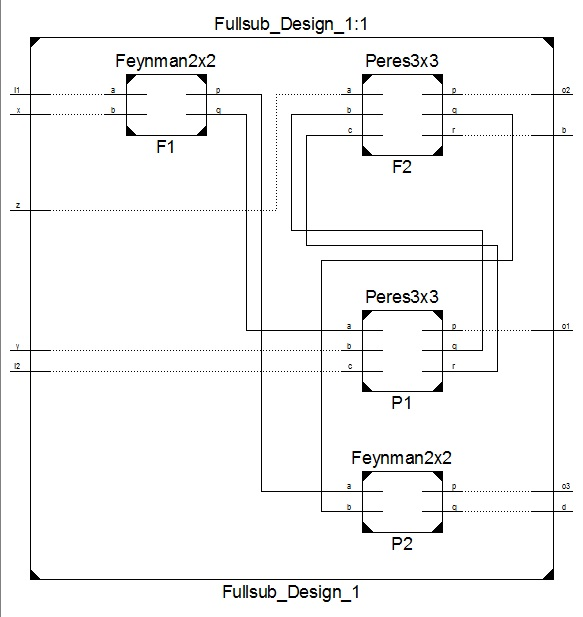
5) 使用佩雷斯和费曼门的全减器：

当使用两个佩雷斯门和两个费曼门设计全减器时， F1=1的A和F2=0的C如图12所示。

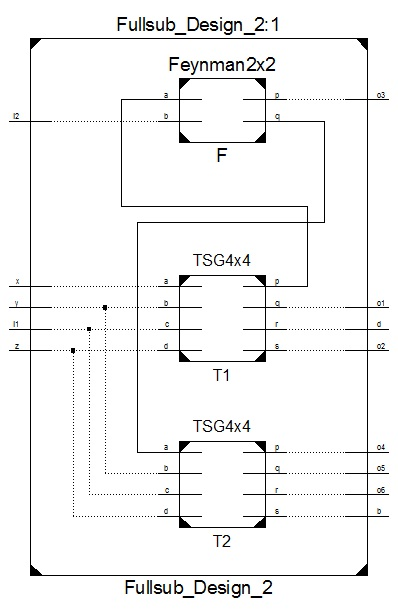
6) 使用TSG和费曼门的全减器：

当使用两个TSG和一个费曼门设计全减器时，T 1=0的C和F=1的B如图13所示。

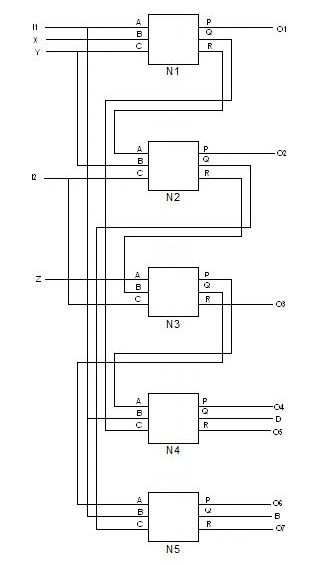
7) 使用NG门的全减器：

如图14所示，当A为N1=1且C为N2=0时，使用五个NG可逆门设计了全减器。

VI. 仿真结果与讨论

加法器和减法器电路在Xilinx ISE 9.2i软件工具中进行设计和仿真。

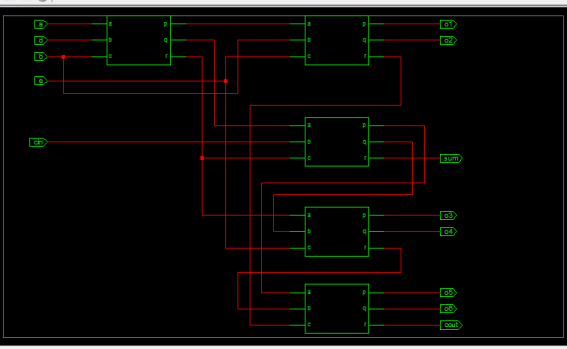
A. 使用托佛利门的全加器设计

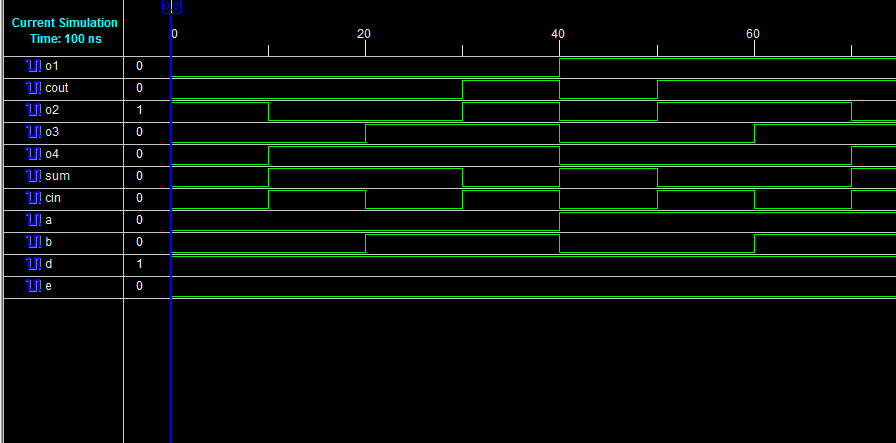
图15和图16分别描述了全加器设计的RTL原理图和仿真波形。

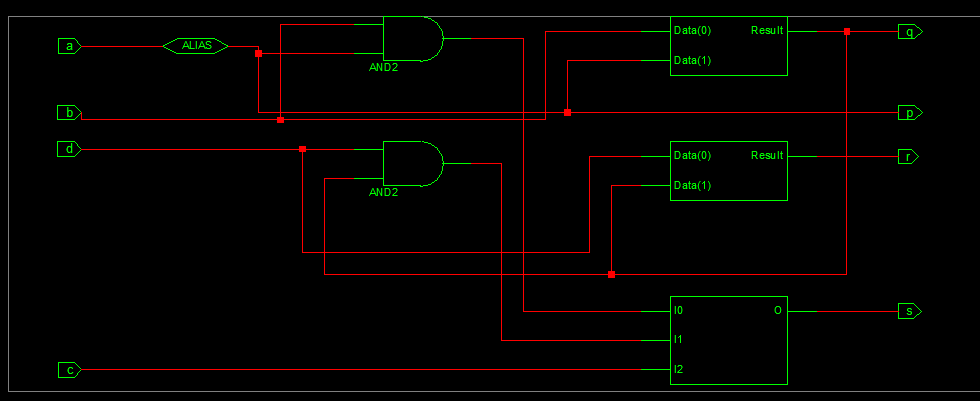
B. 使用弗雷德金门的全加器设计

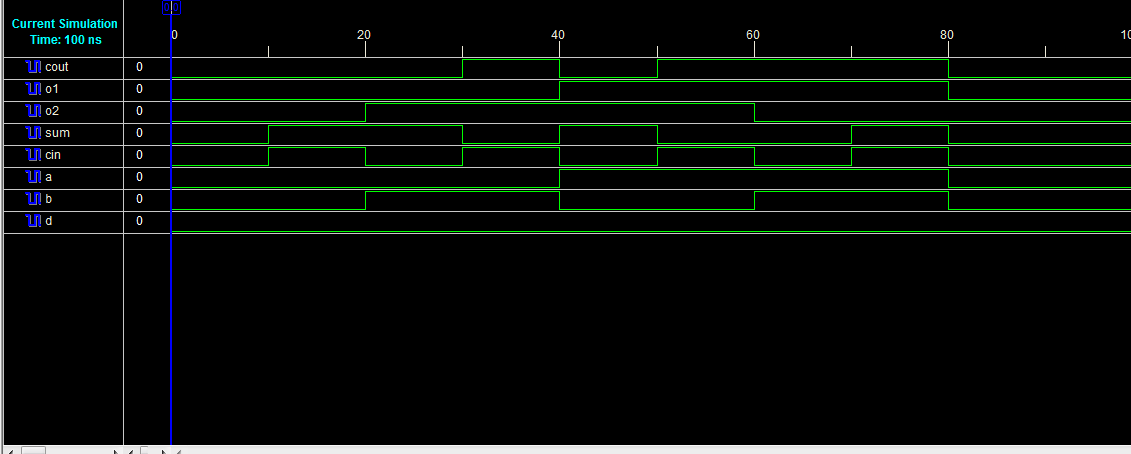
图17和图18分别描述了全加器设计的RTL原理图和仿真波形。

C. 使用双Peres门的全加器设计

图19和图20分别描述了全加器设计的RTL原理图和仿真波形。

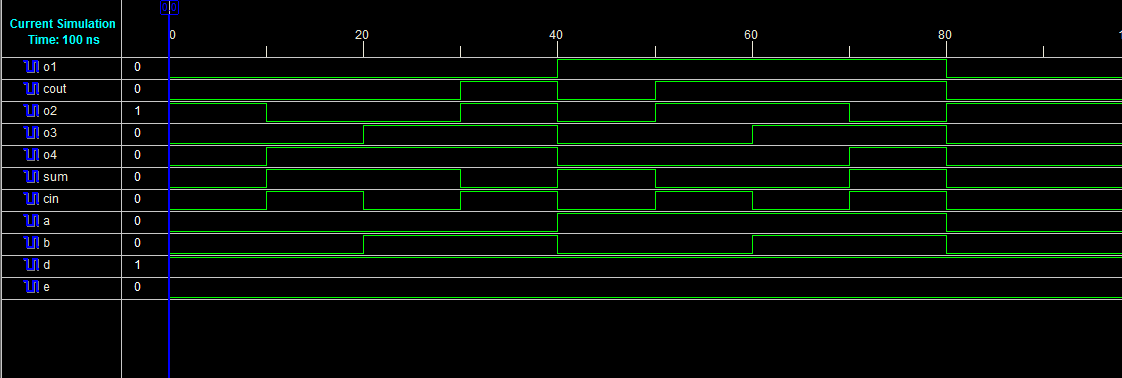
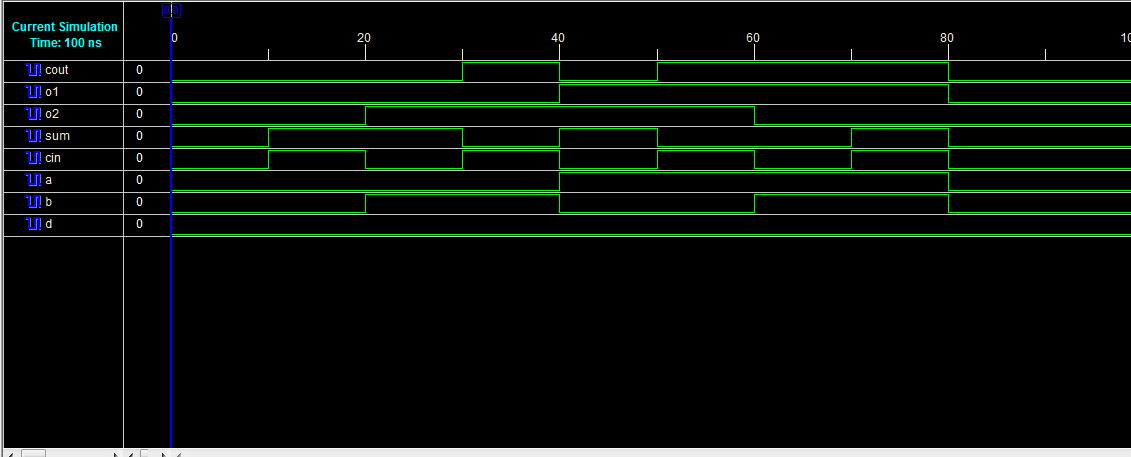
D. 使用TSG门的全加器设计

图21和图22分别展示了全加器设计的RTL原理图和仿真波形。

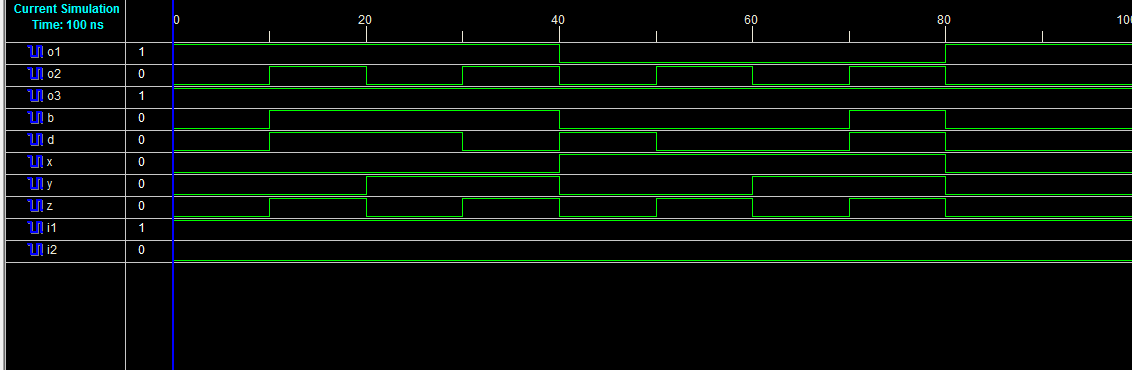
E. 使用佩雷斯和费曼门的全减器设计

图23和图24分别描述了全减器设计的RTL原理图和仿真波形。

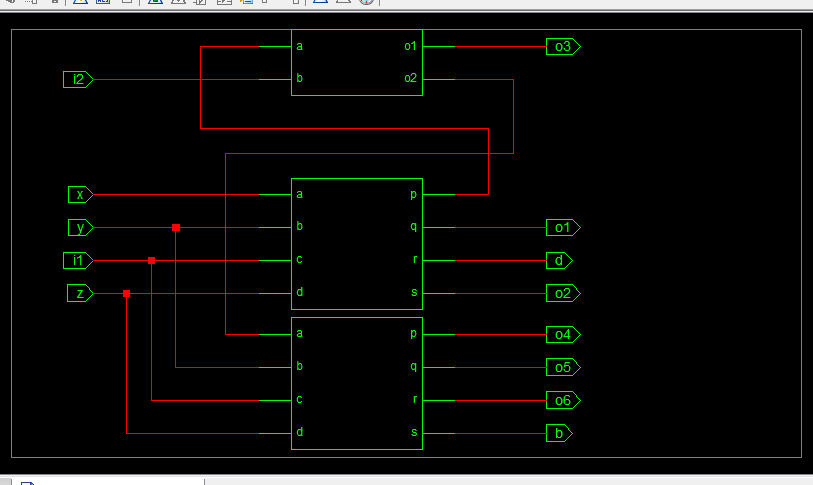
F. 使用TSG和费曼的全减器设计

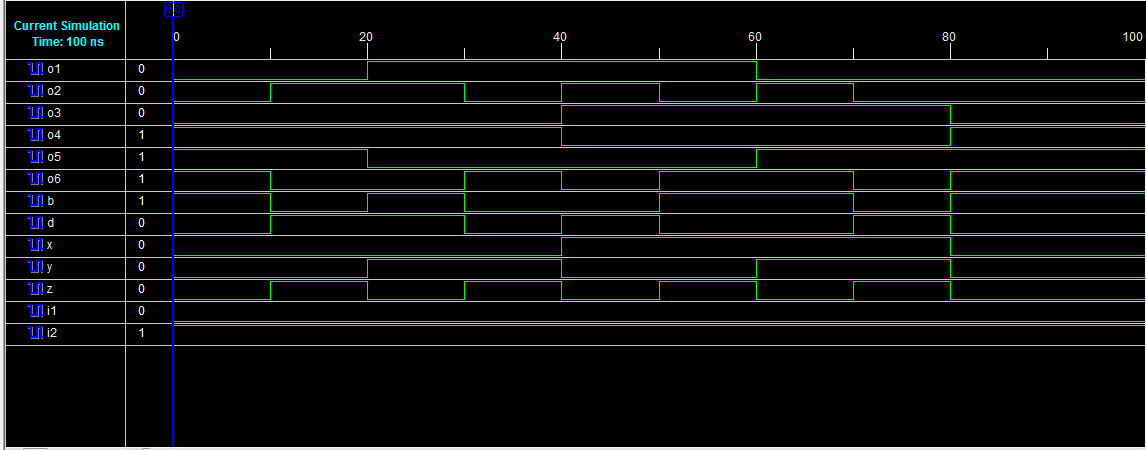
全减器设计的RTL原理图和仿真波形分别如图25和图26所示。

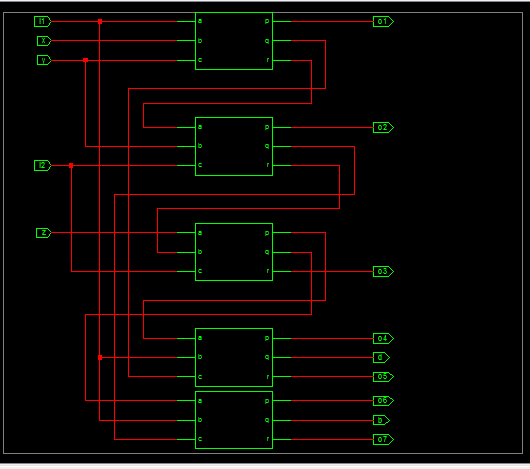
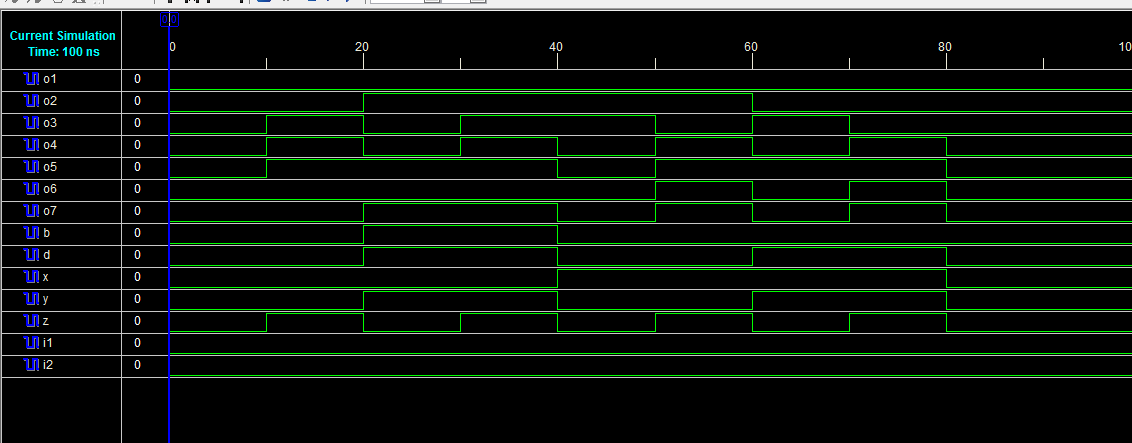
G. 使用新门（NG）的全减器设计

图27和图28分别描述了全减器设计的RTL原理图和仿真波形。

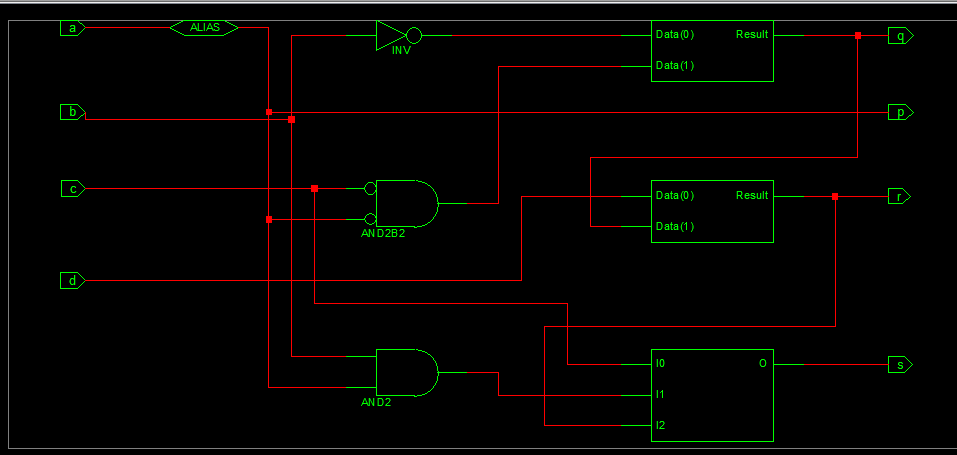
H. 性能分析

本文提出的工作展示了基于现有可逆门设计的各种可逆逻辑加法器和减法器的比较研究；比较内容包括使用的门数量、垃圾输出和量子代价，如表I所示。

设计类型	门数量	垃圾输出数量	量子代价
使用托佛利门的全加器	6	20	25
使用弗雷德金门的全加器	4	10	25
使用DPG门的全加器	2	14	4
使用TSG门的全加器	2	15	4
全减器 使用佩雷斯和费曼门	3	20	10
全减器 使用TSG和费曼门	6	33	9
全减器 使用NG门	7	45	20

VII. 结论

本文提出了一些新颖的设计，利用从文献中收集和讨论的现有可逆逻辑门来实现数字电路中的加法器和减法器。我们在此得出结论：DPG可逆门具有最小的量子代价和垃圾输出，同时在构建全加器时使用的门数量最少。

该论文可进一步扩展至利用可逆逻辑进行更复杂的组合和时序电路的数字设计开发。通过在SPICE中实现设计，可计算功耗和延迟。还可使用更多类型的可逆逻辑门计算量子代价，从而分析性能并与相应的不可逆逻辑设计进行比较。