MEMS传感器读出电路设计与仿真

MEMS传感器读出电路的设计与仿真

一、引言

微机电系统（MEMS）是由机电元件和微型机械元件（即通过微加工技术制造的器件和结构）组成的系统。这些MEMS器件或结构的尺寸通常在0.02到1.0毫米之间。它们包含一个用于处理数据的中央单元——微处理器，以及多个与周围环境相互作用的其他组件，如微执行器和微传感器。

传感器能够检测事件或物理量的变化，并提供相应的输出，通常为电信号或光信号。MEMS传感器（如陀螺仪、麦克风）在汽车、消费电子、工业等领域具有广泛的应用。设计和制造具有高灵敏度和精度的这些传感器是一项主要挑战。采用MEMS技术制造的传感器优于传统传感器，原因在于：尺寸更小（20微米至毫米级）；低功耗；对输入变化的灵敏度更高；由于大规模生产而更具经济性；以及在耳内植入物（人工耳蜗植入体）、航天等新兴领域的应用。技术等需求无法通过传统传感器实现。

传感器本身无法直接与现实世界连接，因此需要为 MEMS传感器配备读出电路。大多数MEMS传感器基于电容式传感原理工作，其中接口电子电路需要检测飞法至阿法拉第量级的微小电容变化。

读出电路的目标是检测该电容变化并将其转换为等效电压。MEMS传感器相对于被测物理变量所产生的电容变化非常小，因此需要开发信号调理电路，将微小的电容变化转换为可测量的电压信号。目前有多种方法可用于提取传感器输出，如谐振法、振荡器法、充放电法、调制解调方法[1]等。

本文采用调制解调方法来设计读出电路，因为该方法适用于高分辨率和高带宽的应用。在参考文献[2]中，作者使用该技术来检测MEMS加速度计的加速度。基于CTV传感方法的专用集成电路对系统中存在的寄生效应具有较强的鲁棒性，在增益为10时表现出30毫伏/飞法的静态灵敏度。此外，MS3110专用集成电路表现出30毫伏/克的灵敏度，集成该专用集成电路的传感器能够检测低至50毫克的振动。参考文献[2]发现，与其他方法相比，采用调制‐解调方法具有优势。

上述方法需要使用一个稳定的调制电。在对信号进行调制后，读出电路的下一阶段是解调电路。文献[4]中使用斩波器作为解调器，并采用了Dickson型DC‐DC电压转换器，使得电容式麦克风在极低的电源（偏置）电压下仍具有极高的灵敏度。在未对麦克风施加偏置电压、电源电压为1.9‐2.0 V时，产生的等效噪声水平为26‐28 分贝(A)。根据文献可知，将斩波器作为解调器也是传感器读出电路中一种可行的解调电路方案。但在选择与MEMS传感器配合使用的接口电路时，还需考虑若干问题。

需要考虑的问题之一是提高传感器的灵敏度。在[5]中，作者开发了一种电路，其中使用电荷放大器来最小化灵敏度损失。但这种方法的权衡是会增加电路中的噪声成分。为了解决这一问题，作者建议使用电压放大器。

如果采用平衡配置电路，例如差分对的情况，噪声成分也可以最小化。在参考文献[6]中，成功演示了一种用于CMOS‐MEMS传感器应用的低噪声、低电荷注入和低时钟馈通的差分CMOS开关斩波电路。通过Cadence仿真验证了该电路的工作原理及其更低的噪声和失调性能。所设计的电路适用于需要更高斩波频率的斩波放大器模块实现。

考虑到这些选项，本文作者对四种不同的解调电路进行了比较。论文的第二部分介绍了吉尔伯特单元作为混频器的设计方法，第三部分给出了所有的仿真结果。最后，作者对结果进行了分析并提出了未来展望，以此作为全文的总结。

II. 设计方法

为了设计读出接口，我们需要了解各种MEMS传感器输出的感知值范围。在本文中，作者考虑了一组时钟脉冲以及来自MEMS传感器的感知信号，该感知信号为交流电桥网络输出的纯正弦波形式。

本文针对一种应用展开，该应用中需要对信号进行调制以保护低频感知信号，并将其解调还原。吉尔伯特单元乘法器通常作为一种混频器，将两个频率混合以产生中频[7]。该混频器可分别将信号上变频或下变频至较高或较低的频率。

乘法过程通过将两个信号相乘开始，

$$
(1)\quad s_1(t) = A_1 \cos(\omega_1 t + \phi_1)
$$
$$
(2)\quad s_2(t) = A_2 \cos(\omega_2 t + \phi_2)
$$

结果中的多路信号将是，

$$
(3)\quad s_{out}(t) = \frac{A_1 A_2}{2} [\cos((\omega_1 + \omega_2)t + \phi_1 + \phi_2) + \cos((\omega_1 - \omega_2)t + \phi_1 - \phi_2)]
$$

其中，$\omega_1$和$\omega_2$是输入信号的频率，$\phi_1$和$\phi_2$是输入信号的相位分量。

吉尔伯特单元混频器是一种双平衡混频器，相较于单平衡实现，它能够消除本振到中频、射频到中频的泄漏，从而提高线性度。作为调制器的吉尔伯特单元乘法器设计需满足以下规格：

• $V_{dd} = 1.8V$
• $V_{ss} = -1.8V$
• 输入频率范围：100 kHz
• 时钟脉冲：1 MHz

假设所有晶体管均工作于饱和区，漏极电流方程可表示为：

$$
(4)\quad I_D = \frac{1}{2} \mu C_{ox} \frac{W}{L} (V_{gs} - V_{tn})^2
$$

对于上拉晶体管我们有：

$$
(5)\quad g_m = \sqrt{2 \mu C_{ox} (W/L) I_{ss}}
$$

其中，
$g_m$ = 跨导，
$\mu$ = 迁移率常数，
$C_{ox}$ = 氧化层电容，
$W$ = 器件宽度，
$L$ = 器件长度，
$I_{ss}$ = 尾电流，
$V_{tn}$ = NMOS晶体管阈值电压。

从 gpdk 180纳米 模型文件中获得了以下 参数 值：

• $\mu = 400\ cm^2/V\cdot s$
• $T_{ox} = 4 \times 10^{-9}\ m$
• $\varepsilon_o = 8.854 \times 10^{-12}\ F/m$

因此获得为

$$
C_{ox} = \frac{3.9 \varepsilon_o}{T_{ox}} = 8.637 \times 10^{-7}\ F/m^2
$$

为了使吉尔伯特乘法器作为混频器工作，前六个晶体管必须具有相同的宽长比，并且电流在每个支路中均等分配。尾电流可以从公式(6)中求得。

$$
(6)\quad I_{ss} = \frac{V_{in}}{R}
$$

$g_m$ 的计算是通过假设线性比例下的电压增益（$A_c$）约为 2 得出的。

$$
(7)\quad A_c = g_m R
$$

其中，$R$ = 为输出阻抗。

利用(6)和(7)代入(5)，可求得上拉晶体管的宽长比。器件的宽长比如表1所示。

晶体管名称	宽度(μm)	长度(纳米)
M1	4.2	350
M2	0.70	350
M3	0.70	350
M4	1.4	350
M5	1.4	350
M6	1.4	350
M7	1.4	350
M8	3.5	350
M9	3.5	350

解调信号通过低通滤波器进行滤波，以去除高频成分。为此，使用RC滤波器，并通过以下公式计算截止频率：

$$
(8)\quad f_c = \frac{1}{2\pi RC}
$$

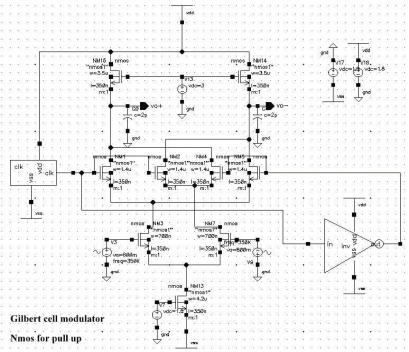
其中，$C$ = 为滤波电容。图1显示了设计的作为调制器的吉尔伯特混频器的原理图。

III. 仿真与结果分析

仿真使用CADENCE VIRTUOSO EDA工具中的ADEL在 gpdk 350纳米技术下完成。

A. 调制器设计

用于调制的吉尔伯特混频器原理图如图1所示。相应的仿真波形如图2所示。调制器模块输入的传感信号为100千赫正弦波，载波信号为频率1兆赫的时钟脉冲。

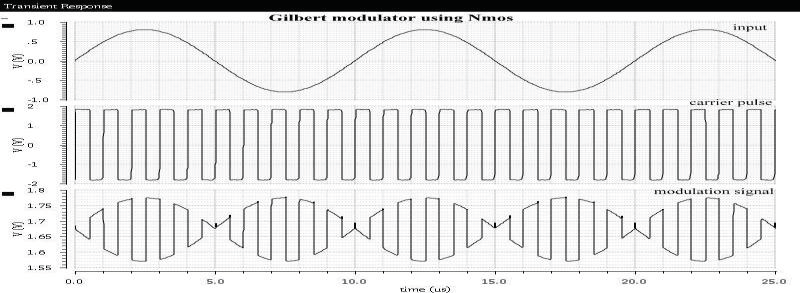
从仿真结果可以看出，输入的100kHz信号经历了无失真的脉冲幅度调制(PAM)。

B. 吉尔伯特混频器作为解调器

对于第一种方法，我们将吉尔伯特单元与另一个吉尔伯特单元级联，以从PAM波中恢复包络。作为解调器的吉尔伯特单元原理图如图3所示。此处时钟脉冲为1兆赫，调制信号为100千赫PAM波。使用RC滤波器滤除解调信号中的高频成分。

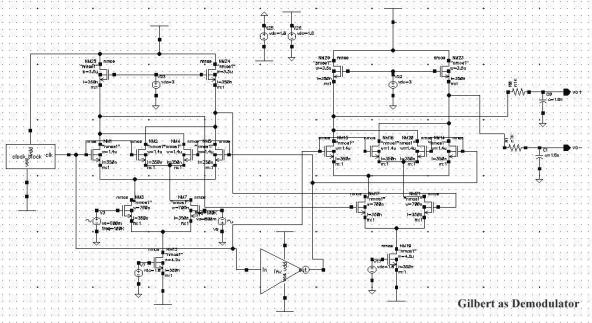
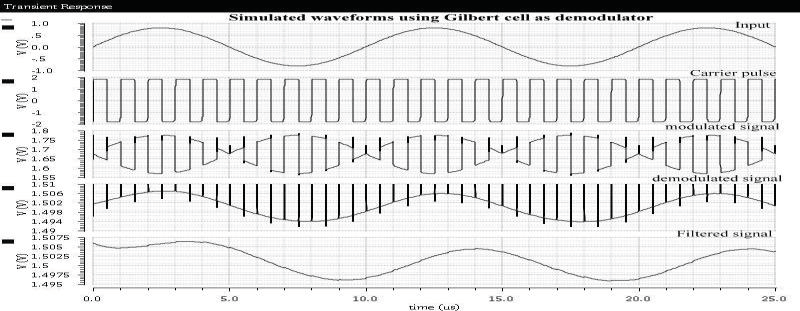
使用吉尔伯特混频器解调信号的仿真波形如图4所示。在解调信号的输出端使用了RC低通滤波器，以滤除解调波形中的所有高频成分。可以看出，滤波后的解调信号与调制信号同相，且失真非常小或可忽略不计。

C. 斩波器作为解调器

斩波电路被作为解调目的的第二种选择。斩波稳定技术已广泛应用于放大器中，利用调制与解调原理来实现闪烁（1/f）噪声和偏移减小的目的。因此，调制与解调电路的功能和性能决定了斩波稳定的实现和达到。在[8]中设计的放大器可用于放大解调信号。对于该原理图，时钟脉冲频率为1兆赫，调制信号为100 KHz PAM波。图5显示了斩波器作为解调器模块的原理图。

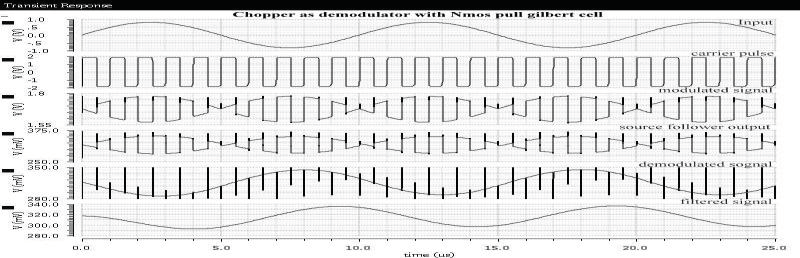
已针对所使用的调制和解调模块的各种配置制作了一个表格，如表2所示。

表2：解调方案之间的比较

参数	吉尔伯特调制 – 吉尔伯特解调 (PMOS下拉)	吉尔伯特调制 – 吉尔伯特解调 (NMOS下拉)	吉尔伯特调制 – 斩波器解调 (PMOS下拉)	吉尔伯特调制 – 斩波器解调 (NMOS下拉)
调制信号输出电平	1.65 伏特	1.68 伏特	1.65 伏特	1.68 伏特
解调信号输出电平	1.41 伏特	1.506 伏特	310 mV	320 mV
差分调制信号强度	522 毫伏峰峰值	406 毫伏峰峰值	522 毫伏峰峰值	406 毫伏峰峰值
差分解调信号强度	28.2 mV p-p	16.82 毫伏峰峰值 p-p	100 毫伏峰峰值	78 毫伏峰峰值
传播延迟（含寄生效应）	1.787 μs	1.943 μs	—	—
传播延迟（不含寄生效应）	1.770 μs	1.896 μs	—	—
寄生效应引起的延迟差	17 ns	47 ns	—	—

参考上表，发现当吉尔伯特单元同时用作调制器和解调器时，其性能优于其他三种配置。在吉尔伯特单元作为调制器、斩波器作为解调电路的配置中，由于其输出电压水平为300毫伏左右，而其他配置的输出电压接近1.5伏，因此必须在输出端使用电压放大器以提升信号电平。

已生成整个读出电路的版图，如图7所示。

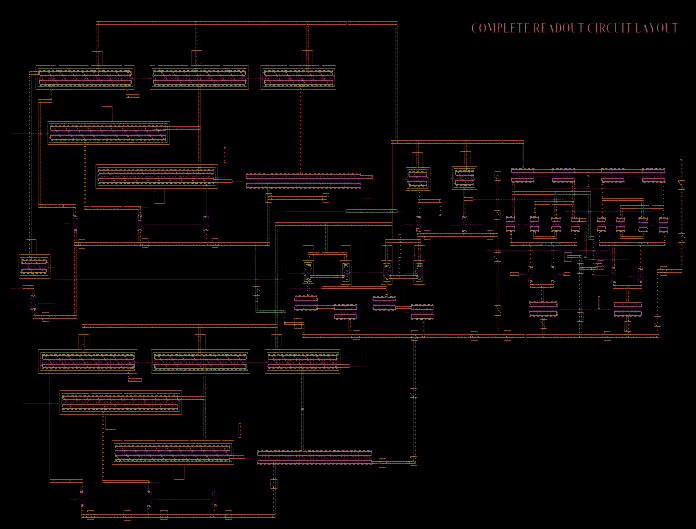
完成版图设计后，经检查未发现DRC错误，并对版图进行了寄生参数提取以获得寄生RC组件。已完成整个读出电路的反标，由此发现读出电路原理图中考虑寄生效应时的传播延迟（1.835μs）与不考虑寄生效应时的传播延迟（1.717μs）之间的差异为118纳秒。

IV. 结论

本文对可用于MEMS传感器读出电路的四种解调方案进行了比较。从表2可以看出，在四种配置中，采用吉尔伯特单元作为调制器和解调器的组合相比其他三种方案具有更好的输出电压水平，达到1.506伏特。

在延迟方面，电路必须具有更小的延迟才能有效运行。将吉尔伯特单元配置为调制器和解调器时，在未连接时钟电路的情况下，其传播延迟较小，为17纳秒。

完整读出电路的总体传播延迟为1.835μs（含寄生效应）和1.717μs（不含寄生效应），两者差异为118纳秒。

V. 未来展望

使用AMS技术的PDK 350纳米技术可以完成读出电路的完整ASIC实现，其掩模文件可与MEMS电容式传感器集成以生成微芯片。通过使用可变电容器（电容阵列）替代单个电容，片上时钟电路可实现动态调节。

本文假设传感信号为纯正弦波，但我们可以使用电容阵列来改变电容，进而改变电压，该电压将作为积分模式下运算放大器的输入信号，以获得脉幅调制波。解调电路可以采用吉尔伯特单元。传感机制也可以是电阻式或压电传感。