C++实现离散傅里叶变换的快速算法(FFT)

最新推荐文章于 2025-06-17 02:53:00 发布

原创最新推荐文章于 2025-06-17 02:53:00 发布 · 2.2k 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#fft #c++ #算法

笔记专栏收录该内容

2 篇文章

订阅专栏

本文详细介绍了如何使用C++实现离散傅里叶变换的快速算法(FFT)，包括步骤解析和代码设计。首先，将原序列转换为逆序；接着，通过分解进行2点DFT运算。然后，按照特定规律进行多级蝶形运算，涉及复数计算和模、辐角的处理。最后，提供了一种以模和辐角形式存储结果的方法。

前言：近期作为小白在学习FFT，故写此文，一来提高对FFT的领悟程度，而来求大神指导。

在这里插入图片描述

三、 FFT的C++代码设计的
1、步骤
（1）将原序列变化为序号为逆序的序列；
（2）设总点数N为2的m次方，那么经过m级分解后就可以进行2点DFT运算。
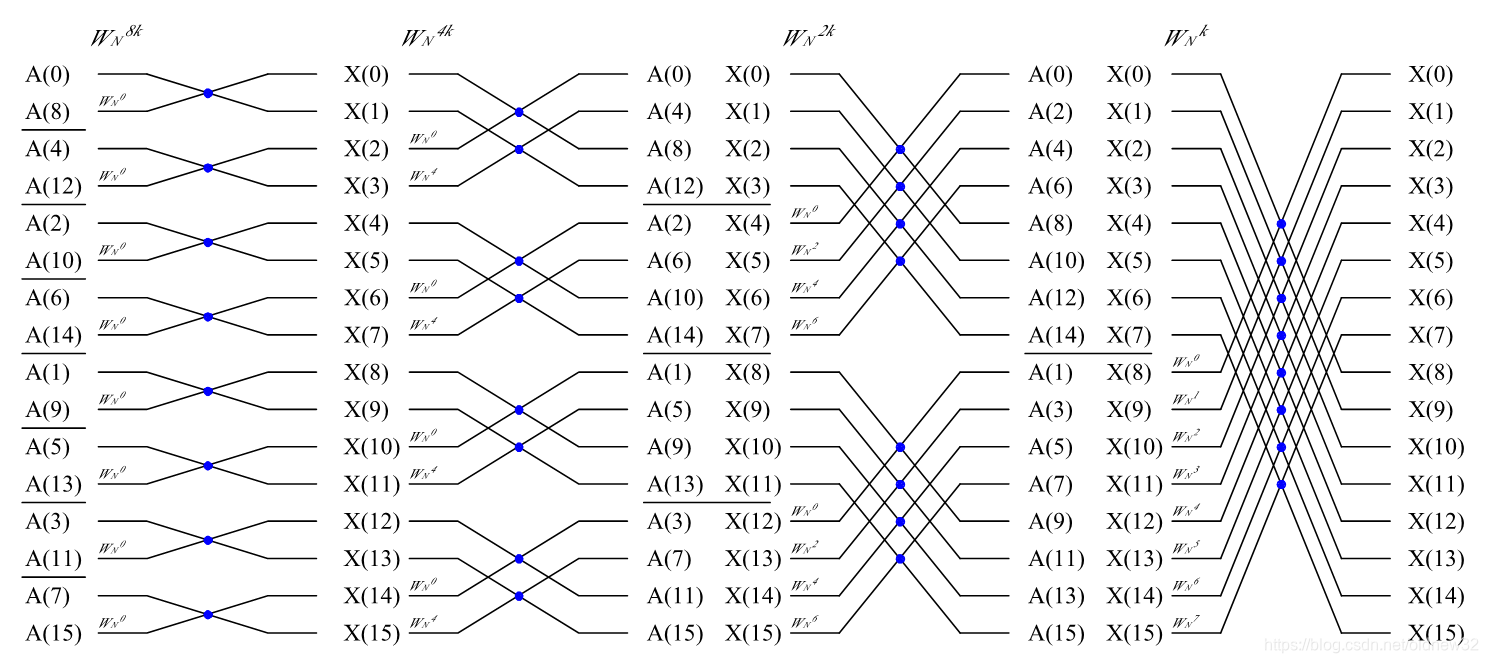
（3）从左到右找规律，对第i级分解（i=0、1、2…m），有规律：①要进行2^{(m-1-i)组蝶形运算②每组蝶形运算依次进行2}i次运算③2组蝶形运算之间的序号间隔为2^(i+1) ,④每组蝶形运算内部2个数之间的序号间隔为2^i。
（4）由于蝶形运算是复数计算。因此可以选择将最终结果表达为模和辐角的形式，也可以表达为实部和虚部的形式，通常选择前者。本文采取的是输出2个数组，1数组个存储幅值（模），1个数组存储辐角。取出即将进行蝶形计算的2个数，分解成实部和虚部的形式，计算旋转因子。根据蝶形运算规则完成计算，再将实部和虚部形式转换成模和辐角的形式

/*
1、amp：幅值存储空间；phase：相位存储空间,
2、m：存储长度为2^m次（m >=1 ），在函数外保证
*/
void FFT(double *amp , double *phase , int m )
{
	double	pi = 3.14159265358979323846 ;  //定义π的值

	//将数据序列按逆序排列
	double	temp ;
	int		i_temp ;	//中间临时数据
	int		nixu ;		//数据的逆序下标

	// 1<<m 即 2^m
	for (int i = 0 ; i < (1<<m) ; i++)
	{
		i_temp	= i ; // i是顺序下标
		nixu	= 0 ; // 逆序下标
		for (int j = 0; j < m; j++)
		{
			nixu	= nixu << 1 ;				// 逆序下标向左移一位，腾出最低位，准备接收数据
			nixu	= nixu | (i_temp & 0x01) ;	// 将顺序下标的的最低位取出放到逆序下标的最低位上
			i_temp	= i_temp >> 1 ;				// 顺序下标向右移一位，准备下次取最低位		
		}
		//按顺序下标的顺序依次计算逆序下标后，将顺序、逆序位置的数据交换。
		//出现顺序下标的值大于逆序下标时就不交换，因为在顺序下标小的时候已经交换过了。
		if ( nixu > i)
		{
			temp = *(amp + i) ;
			*(amp + i) = *(amp + nixu);
			*(amp + nixu) = temp ;			
		}
		*(phase + i ) = 0 ;  // 相位数据置0
	}
	
	// 最外层循环，按分解的级数进行循环
	double	real_X1 , real_X2 ,real_T1 ,real_T2 ;
	double	imag_X1 , imag_X2 ,imag_T1 ,imag_T2;
	double	rad_WnK = 0 ;
	int		D1 , D2 , index1 , index2;
	// 分解为m级
	for (int i = 0; i < m; i++)
	{
		D1 = 1<< i ;	//	2^i		//  蝶形计算内部2个数的序号间隔
		D2 = 2<< i ;	//	2^(i+1) //	两组蝶形计算间的序号间隔
		
		// j < nLength/2^(i-1) ;
		for (int j = 0; j < (1<<(m-1-i)); j++)
		{
			for (int k = 0; k  < (1<< i); k ++)
			{
				rad_WnK =	0 - k * pi / ( 1<< i ) ; //旋转因子的角度
				index1	=	D2 * j + k  ;		// 蝶形运算第一个数的下标
				index2	=	D2 * j + k + D1 ;	// 蝶形运算第二个数的下标
				//蝶形运算第一个数的实部和虚部
				real_X1	=	*(amp + index1 ) * cos( *(phase + index1)) ;
				imag_X1	=	*(amp + index1 ) * sin( *(phase + index1)) ;
				//临时存储蝶形运算第一个数的实部和虚部
				real_T1	=	real_X1 ;
				imag_T1	=	imag_X1 ;
				//蝶形运算第二个数的实部和虚部
				real_X2	=	*(amp + index2 ) * cos( *(phase + index2)) ;
				imag_X2	=	*(amp + index2 ) * sin( *(phase + index2)) ;
				//蝶形运算第一个数乘以旋转因子后的实部和虚部
				real_T2	=	*(amp + index2 ) * cos( *(phase + index2) + rad_WnK ) ;
				imag_T2	=	*(amp + index2 ) * sin( *(phase + index2) + rad_WnK ) ;
				
				//蝶形运算主体
				real_X1 = real_X1 + real_T2 ;
				imag_X1 = imag_X1 + imag_T2 ;
				real_X2 = real_T1 - real_T2 ;
				imag_X2 = imag_T1 - imag_T2 ;
				// 将实部、虚部转换成模和角
				*(amp + index1 )	= sqrt(real_X1 * real_X1 + imag_X1 * imag_X1) ;
				
				//处理模为0的情况
				if (*(amp + index1 ) < 1E-100 )
				{
					*(amp + index1 ) = 1E-100 ;
				}

				*(phase + index1 )	= acos( real_X1 / *(amp + index1 ) ) ;

				if (imag_X1 < 0)
				{
					*(phase + index1 ) = 0 - *(phase + index1 ) ;
				}

				*(amp + index2 ) = sqrt(real_X2 * real_X2 + imag_X2 * imag_X2) ;

				//处理模为0的情况
				if ( *(amp + index2 ) < 1E-100)
				{
					*(amp + index2 ) = 1E-100 ;
				}

				*(phase + index2 )	= acos( real_X2 / *(amp + index2 ) ) ;

				if (imag_X2 < 0)
				{
					*(phase + index2 ) = 0 - *(phase + index2 ) ;
				}
			}
		}
	}	
}