一种任意位的二进制逆序算法

最近学习FFT算法，用到逆序算法，我参照大神们的思想，自己做了一个，就叫“糖葫芦法”吧，就像吃糖葫芦一样一颗一颗地吃，吃完后肚子里的糖葫芦就是逆序排列的，请大神指导。
方法描述如下：
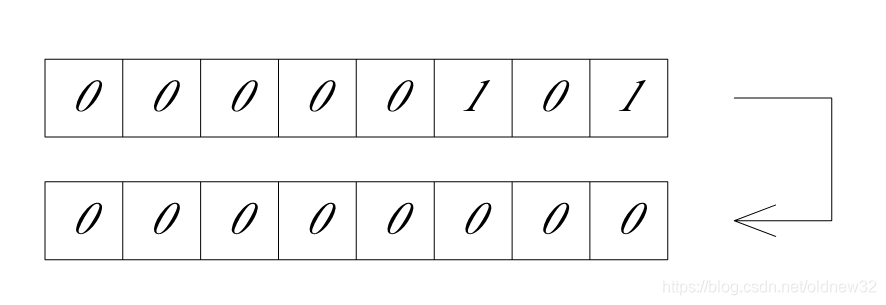
（1）复制原变量的最低位，粘贴到结果变量的最低位。
（2）再将原变量右移一位，将结果变量左移一位，重复复制，粘贴过程。
（3）如此循环，直到完成规定位的数据逆序。

// 整数的任意位数的二进制逆序
int		NiXu(int inData , int b) 
{
	int	mask	= 0x00		;
	int	data	= inData	;	//输入数据
	int result	= 0x00		;	//输出数据

	// b 为需要逆序的位数
	for (int i = 0; i < b; i++)
	{
		result	= result << 1 ;		// 结果向左移一位
		mask	= data & 0x01 ;		// 取数据最低位
		result	= result | mask ;	// 将数据的最低位放到结果的最低位上
		data	= data >> 1 ;		// 数据向右移一位		
	}
	return result;
}