本文深入讲解了矩阵的基本概念，如方阵、行向量、列向量，以及矩阵的加法、减法、乘法运算规则。同时，文章还探讨了矩阵的迹、转置、对称矩阵等高级特性，并提供了详细的数学公式和运算示例。
本课程来自深度之眼，部分截图来自课程视频。
【第一章 线性代数】1.1矩阵及其运算合集
虽然是数学基础，但是有些很基础的就略过。。。例如什么叫方阵，什么是行向量之类，但是提纲会列出来。一些基本的证明也pass。
在线LaTeX公式编辑器
任务详解：
本节课主要介绍了矩阵的基本概念及意义，矩阵的基本运算(加，减，乘)，矩阵的迹(方阵)，矩阵的转置，对称矩阵(方阵)等知识点。
掌握目标：
1、了解矩阵的基本概念以及矩阵的意义
2、掌握矩阵的加法减法乘法(包括数乘)，以及两个矩阵能做上面运算的条件
3、 矩阵是否满足交换律和结合律
4、掌握矩阵的转秩和性质，以及对称矩阵
1.矩阵的基本概念以及意义
矩阵及其运算
矩阵
定义1由m×n个数
a
i
j
(
i
=
1
,
2
,
…
,
m
;
j
=
1
,
2
…
,
n
)
a_{ij}(i=1,2,…,m;j=1,2…,n)
aij(i=1,2,…,m;j=1,2…,n)排成的m行n列的数表称为m行n列矩阵，简称m×n矩阵。为表示它是一个整体，总是加一个括弧，并用大写黑体字母表示它，记作
方阵
m=n
行向量
m=1
列向量
n=1
两个矩阵相等
两个矩阵的每一个对应位置上的元素都相等
零矩阵O
所有元素都是0
特殊矩阵
单位矩阵E：对角线上都为1，其他位置都为0的方阵
对角矩阵：是一个主对角线之外的元素皆为0的方阵
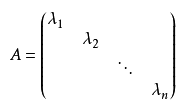
通常记为：
d
i
a
g
(
λ
1
,
λ
2
,
.
.
.
λ
n
)
diag(\lambda_1,\lambda_2,...\lambda_n)
diag(λ1,λ2,...λn)
2.矩阵的基本运算（加，减，乘）
矩阵加法要注意两个矩阵大小要一样（同型矩阵）
矩阵乘法经常用到，要注意两个矩阵的shape，第一个矩阵的列数和第二个矩阵的行数要相等。
设
A
=
(
a
i
j
)
A=(a_{ij})
A=(aij)是一个m×s矩阵，
B
=
(
b
i
j
)
B=(b_{ij})
B=(bij)是一个s×n矩阵，那么规定矩阵A与矩阵B的乘积是一个m×n矩阵
C
=
(
c
i
j
)
C=(c_{ij})
C=(cij)，其中
c
i
j
=
∑
k
=
1
s
a
i
k
b
k
j
c_{ij}=\sum_{k=1}^sa_{ik}b_{kj}
cij=∑k=1saikbkj（就是第一个矩阵第i行的元素（有s个）与第二个矩阵第j列的元素（有s个）逐个相乘后求和）
矩阵的乘法不满足交换律：
A
B
<
>
B
A
AB<>BA
AB<>BA
但是对于单位矩阵E有：
E
A
=
A
E
=
A
EA=AE=A
EA=AE=A，可见单位矩阵E在矩阵乘法中的作用类似于数1.
3.矩阵（方阵）的迹trace
矩阵（方阵）A的迹记为：
t
r
(
A
)
=
∑
i
a
i
i
tr(A)=\sum_ia_{ii}
tr(A)=∑iaii，方阵A的迹为主对角线的元素之和。
虽然：
A
B
<
>
B
A
AB<>BA
AB<>BA，但是：
t
r
(
A
B
)
=
t
r
(
B
A
)
tr(AB)=tr(BA)
tr(AB)=tr(BA)
4.矩阵的转置
把矩阵A的行换成同序数的列得到一个新矩阵，叫做A的转置矩阵，记作
t
r
a
n
p
o
s
e
(
A
)
=
A
T
tranpose(A)=A^T
tranpose(A)=AT。相应的公式有：
(
A
T
)
T
=
A
(A^T)^T=A
(AT)T=A
(
A
+
B
)
T
=
A
T
+
B
T
(A+B)^T=A^T+B^T
(A+B)T=AT+BT
(
λ
A
)
T
=
λ
A
T
(\lambda A)^T=\lambda A^T
(λA)T=λAT
(
A
B
)
T
=
B
T
A
T
(AB)^T=B^TA^T
(AB)T=BTAT
5.对称矩阵（方阵）
设A为n阶方阵，如果满足 A T = A A^T=A AT=A，即 a i j = a j i a_{ij}=a_{ji} aij=aji。那么A称为对称矩阵，简称对称阵。对称阵的特点是：它的元素以对角线为对称轴对应相等。
补充：
如果x，y均是n维列向量，则
x
T
y
=
实
数
x^Ty=实数
xTy=实数，且有
x
T
y
=
y
T
x
x^Ty=y^Tx
xTy=yTx
扫一扫
1524
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
