机器学习理论推导——梯度下降和逻辑回归

 下面介绍梯度下降法：

假设一个线性模型：

为了便于描述，定义：

我们需要选择合适的参数θ0和θ1，使得h(x)和样本中的y尽可能接近。

统计学中，利用最小二乘法可以得到两个参数的解析解：

但是我们将使用计算机科学的常用思想：迭代来求出这两个值，因为在这里模型的简单使得我们非常容易地计算出解析解。实际中我们的模型可能非常复杂，无法求出解析解，因此使用迭代思想是一种通用的解法。

我们的目标和最小二乘法一致，求出代价函数（cost function)：

的最小值，即：

迭代的具体操作是梯度下降法，就是循环调用：

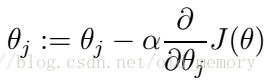
直到收敛，就是θj不再变化，那么必然是J(