该文介绍了一种适用于各种算法的通用攻击方法，涉及离线预计算和在线攻击两个阶段。核心是通过压缩函数R和连接函数g处理密文，寻找可能的密钥。在线阶段，通过不断对比和调整，逐步逼近正确密钥。即使在多次比较未找到匹配时，也能通过递归方式更新候选密钥。
最近在研究这个方法，有一些感悟选择发上来，希望自己的拙见能够帮到大家
本方法属于强力攻击的一种，是可针对各个不同算法的通用攻击方法，因其同时考虑了需付出的时间及空间代价，故得此名。适用范围是选择明文攻击。
本方法的核心公式：.
R为压缩函数，将密文压缩成key所占比特长度。（共S个）
g:为连接函数，表示由得到
(如何得到？其实就是通过公式中的先E后R得到的。兜了一个圈子，表达了同一个意思。猜测创造这个符号可能就是为了方便书写吧...)
本方法分为两个阶段：离线阶段（预计算）和在线阶段
离线阶段：随机选择m个倒霉的key，对其按公式进行运算。如图所示。
但注意，只需要存方块所示部分，即只存每条链表的头和尾。以实现节省储存空间。
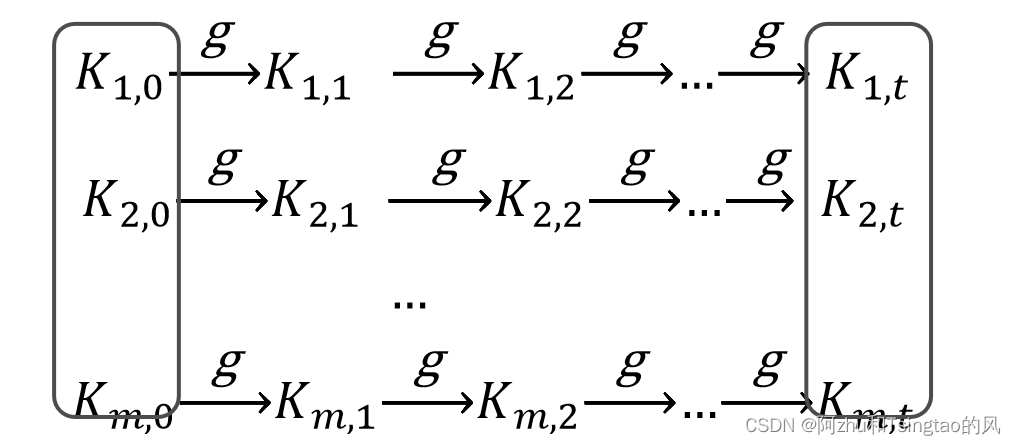
在线阶段：开始攻击，核心思想就是永远和链表的尾部比！
敌手选择明文得到（P,C）
C1和离线阶段中存的表的尾列比：每一个比t次，共S张表，故比较st次。若有一致的，则说明找到了可能的key,这个key就是.原理是什么呢？就是公式！
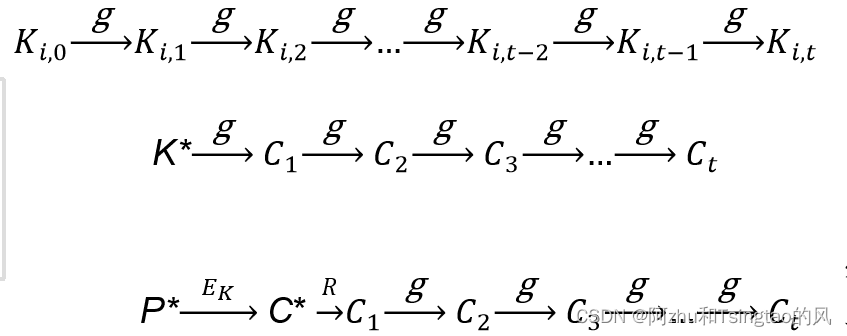
由公式可得，因为对C进行完R操作之后，C就变成了一个K，而这个K又是用上一个K加密P，再压缩得到的，故上一个K就是可能正确的密钥值。
那么问题来了，如果st次比较都没有一样的怎么办？对C1继续做手脚！把C1当作K求得C2，继续和尾列比，如果此时相等，则说明真正的K进行了两次g函数才得到了结果，那么让我们来看K链，发现经过两次g函数得到了尾列，故可能正确的密钥就变成了
.
以此类推
是不是很容易？
扫一扫
2313
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
