一、Clark 变换
1.1 Clark 变换概述
在 FOC (Field Oriented Control,磁场定向控制) 中,Clark 变换是将三相电流信号转换为两相静态坐标系的一个步骤。这个变换是 FOC 控制策略的基础之一。
Clark 变换的主要作用是将三相信号 (A、B、C),其在数学上我们将这三项看做成间隔 120° 的矢量。转换成两个静态坐标系的信号 (α、β) 间隔 90° 的矢量。这可以简化后续的控制计算。
1.2 Clark 变换公式
、
、
= a、b、c 三项原始电流
、
= 变换后的 α、β 电流
1.3 仿真搭建
在这里我们把矩阵形式的 Clark 公式转换为两个等式:
、
、
= a、b、c 三项原始电流
、
= 变换后的 α、β 电流
之后根据这个公式搭建我们的模型:
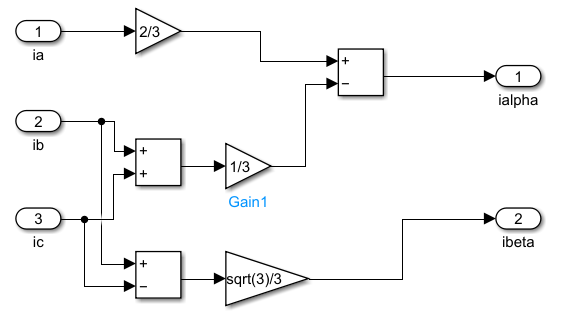
全部模型如下,其中 ThreeCurrGenerator 是我们模拟的三相电机电流:
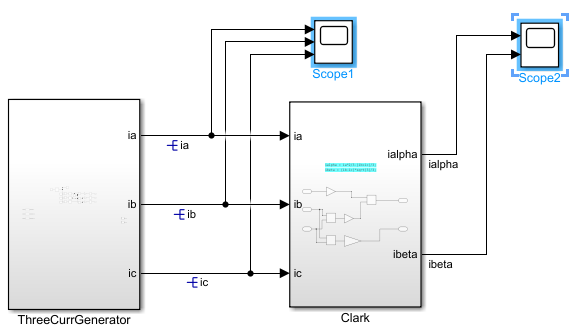
1.4 仿真结果
我们查看上图中的 Scope1 和 Scope2 即可得到当前电流。
1.4.1 三项电流
在 Scope1 中,是我们模拟的电机工作 a、b、c 三项电流:
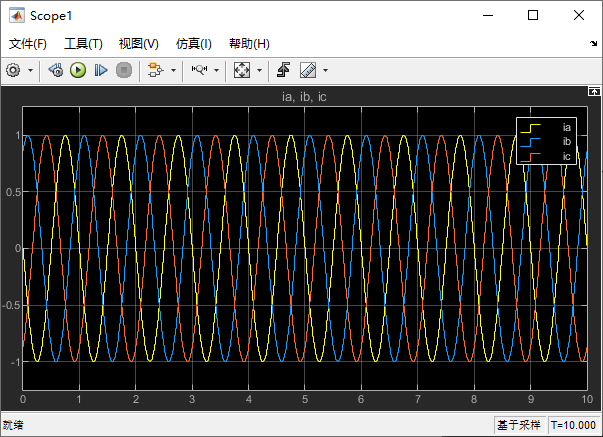
1.4.2 α、β 轴电流
在 Scope2 中,是我们得到的 α、β 轴电流:
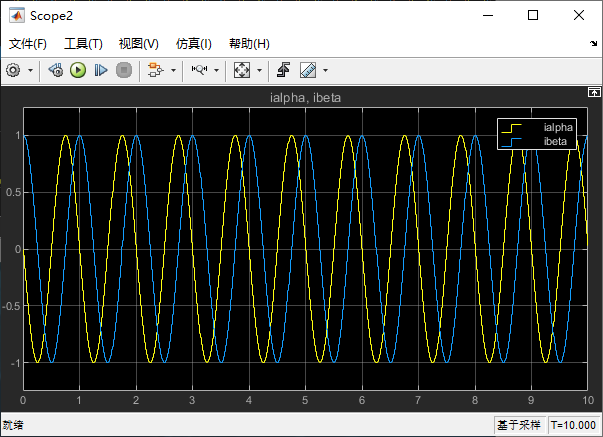
二、Park 变换
2.1 Park 变换概述
Park 变换是电机控制中的一种坐标变换,它将两相静态坐标系 (α-β 坐标系) 的信号转换为旋转坐标系 (d-q 坐标系)。这种变换使得电机的控制更加简便,因为它将电流 (或电压) 信号与电机的磁场对齐,从而使得对转矩和磁场的控制变得更加直观和有效。
通过 Park 变换将这些信号转换为与电机磁场对齐的坐标系,也可以理解为在 α-β 坐标系中剔除了电机信息,即 d-q 坐标系。在 d-q 坐标系中,电机的控制变得更加直观:d 轴 (直轴) 与定子磁场对齐,q轴 (交轴) 则与转矩相关。
2.2 Park 变换公式
、
= α、β 电流
、
= d、q 电流
= 电角度值
2.3 仿真搭建
、
= α、β 电流
、
= d、q 电流
= 电角度值
之后根据这个公式搭建我们的模型:
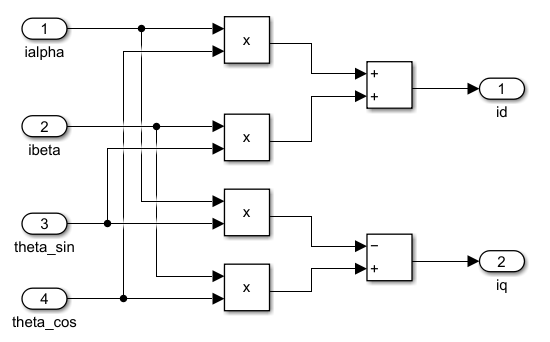
全部模型如下,其中 ThreeCurrGenerator 是我们模拟的三相电机电流:
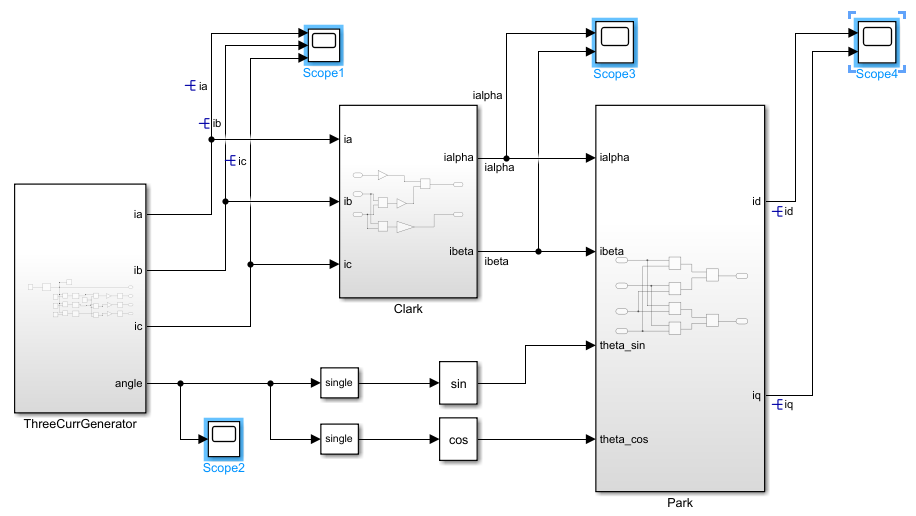
2.4 仿真结果
我们查看上图中的 Scope1、Scope2 和 Scope3 即可得到当前电流。
2.4.1 三项电流
在 Scope1 中,是我们模拟的电机工作 a、b、c 三项电流:
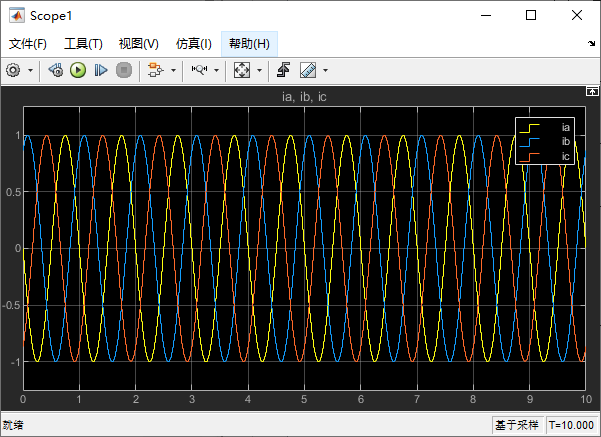
2.4.2 电机角度
Scope3 角度波形显示了我们模拟的角度:
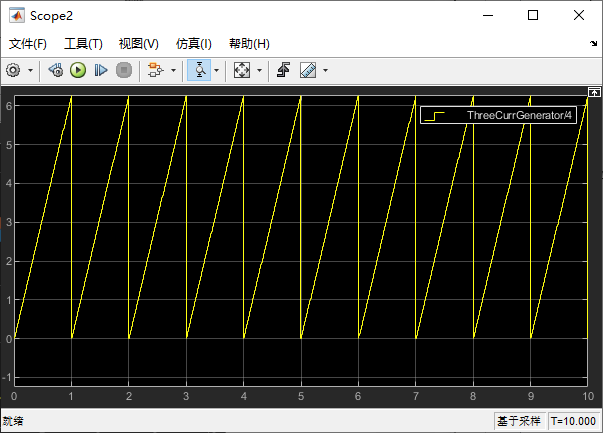
1.4.3 α、β 轴电流
在 Scope3 中,是我们得到的 α、β 轴电流:
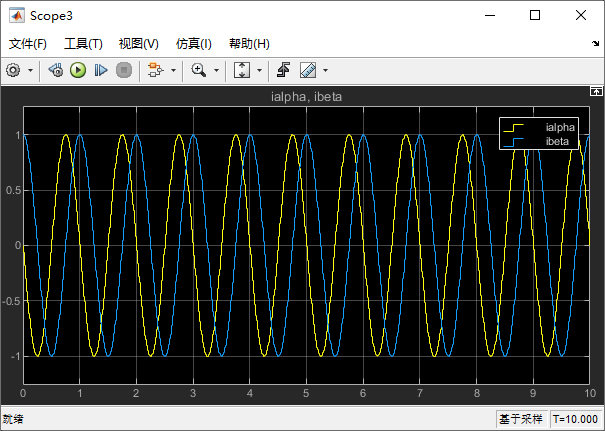
1.4.4 d、q 轴电流
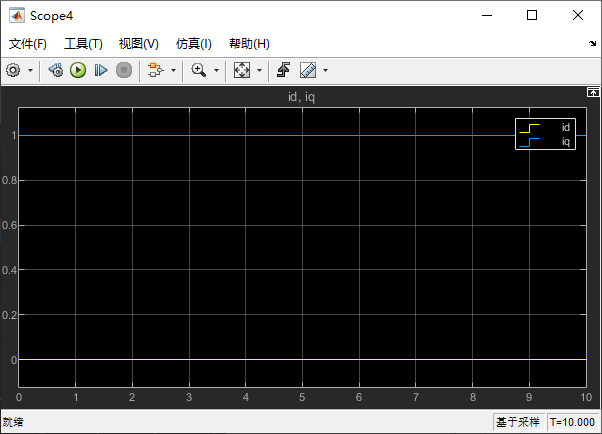
在 Scope4 中,是我们得到的 d、q 轴电流:
三、Park 逆变换
3.1 Park 逆变换概述
Park 逆变换(Inverse Park Transformation)也可以用于将直轴 idi_did 和交轴 iqi_qiq 电流转回到 αβ\alpha \betaαβ 坐标系(通常称为 αβ 轴)。这种变换在变频器控制和电机控制中非常常见,特别是在磁场定向控制(FOC)中。
3.2 Park 逆变换公式
、
= α、β 电流
、
= d、q 电流
= 电角度值
3.3 仿真搭建
、
= α、β 电流
、
= d、q 电流
= 电角度值
根据这个公式搭建我们的模型:
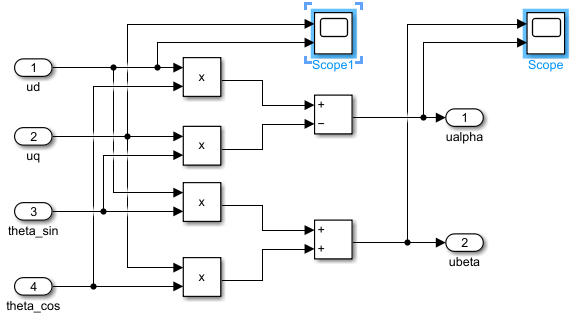
3.4 仿真结果
3.4.1 原始的  、
、 波形
波形
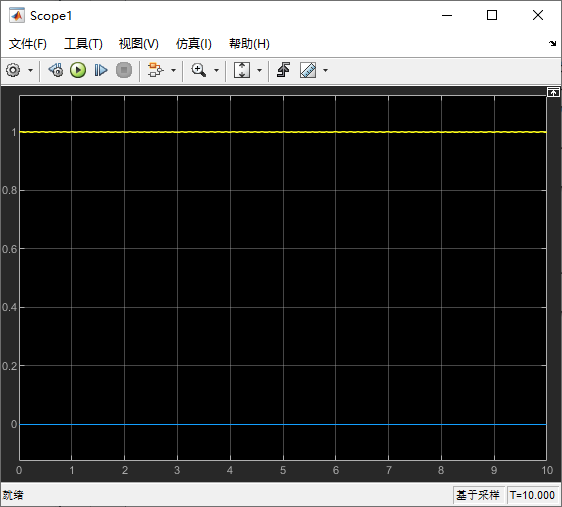
3.4.2 Park 逆变换后的 α、β 波形
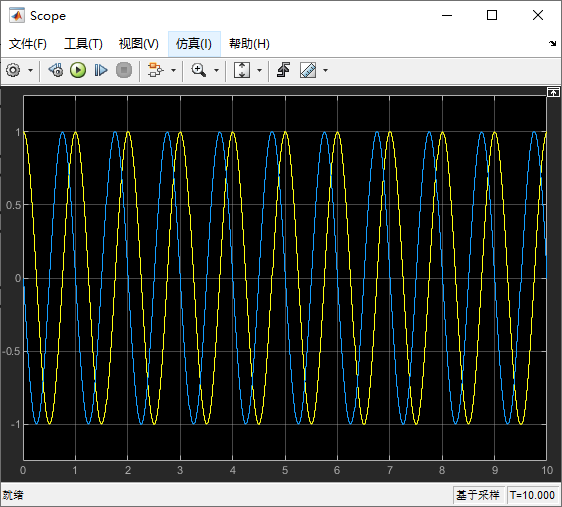
四、SVPWM (零序注入法)
4.1 SVPWM 概述
SVPWM (空间矢量脉宽调制) 是一种常用于三相电机控制 (如无刷直流电机或交流异步电机) 中的调制技术。它的核心目标是提高电机驱动系统的效率和性能。
SVPWM 比 SPWM 的优势除了降低谐波、优化电流、减少电磁干扰等特性外,最大的特点就是提高了电压利用率。
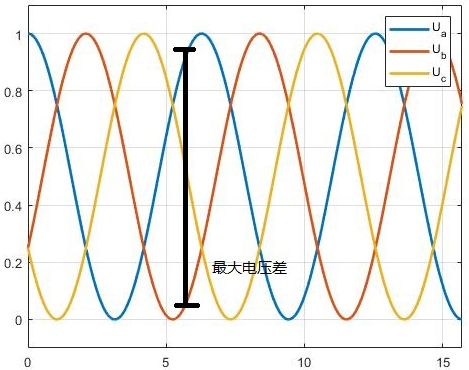
在这种方式驱动下,如果我们测量相电压,也就是 A、B、C 三项与低的电势差,波形会是左图这样。按照图中 1V 为母线电压,在任意两相其最大电压差仅有 0.866V,也就是浪费掉了 13.4% 的电压驱动能力。
所以我们希望做功区域能覆盖整个电压差,这就需要 SVPWM 技术了,他的输出波形会是一个马鞍面,也就是右图:
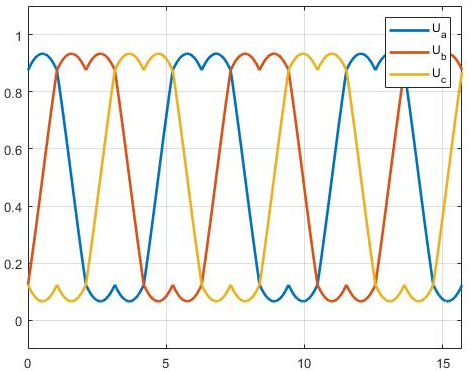
4.2 零序注入法概述
通过给三相参考电压同时加一个公共偏置电压 (零序电压),让三相参考波形整体上移或下移,从而让参考电压更接近六边形边界,使逆变器的 DC 母线得到最大利用。
在下图中,正弦波是我们的 SPWM 波形;中间的三角波是我们的注入量;马鞍波是注入后的SVPWM 波形。可见,在同等的输出电压情况,SVPWM 的电压峰值要比 SPWM 的峰值低 0.2V。
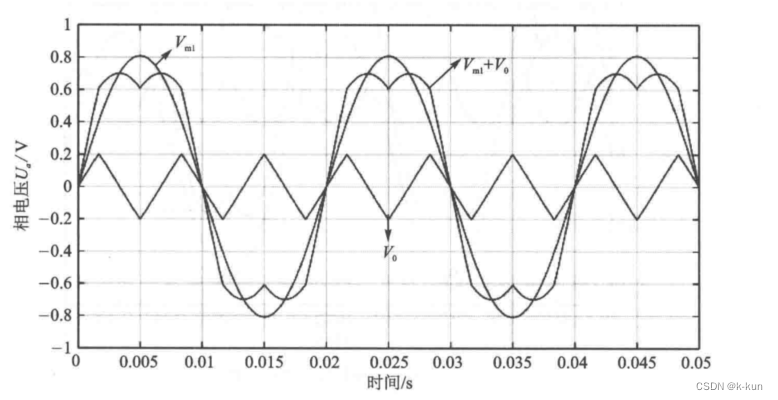
4.3 零序注入法公式

、
、
= 三相电的相电压 (线对地电压)
= 相电压峰值
、
、
= 电压120°的超前后滞后
= 零序分量
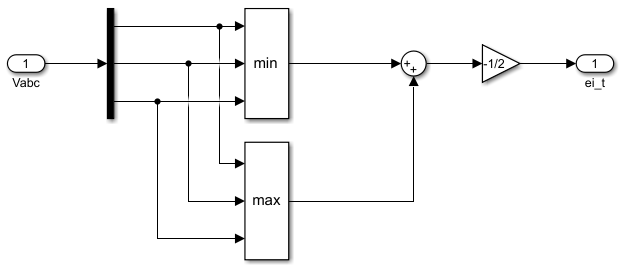
其中零序分量公式如下:
= 当前三相中最大的电压
= 当前三相中最小的电压
4.4 仿真搭建
根据零序分量公式搭建模型:
= 当前三相中最大的电压
= 当前三相中最小的电压
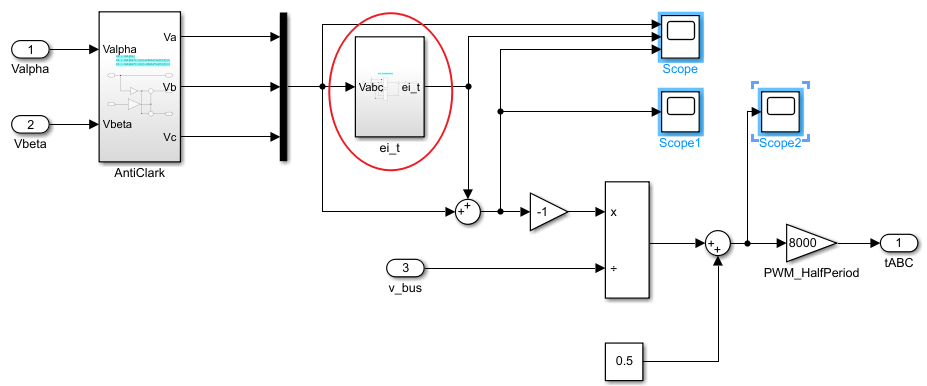
将 Valpha,Vbeta 进行逆 Park 变换,得到三项电压。之后除以 v_bus,得到一个 -0.5~0.5 的电压值,之后加上 0.5 其乘 8000 也就是 PWM 其所需要的寄存器 crr 值。
4.5 仿真结果
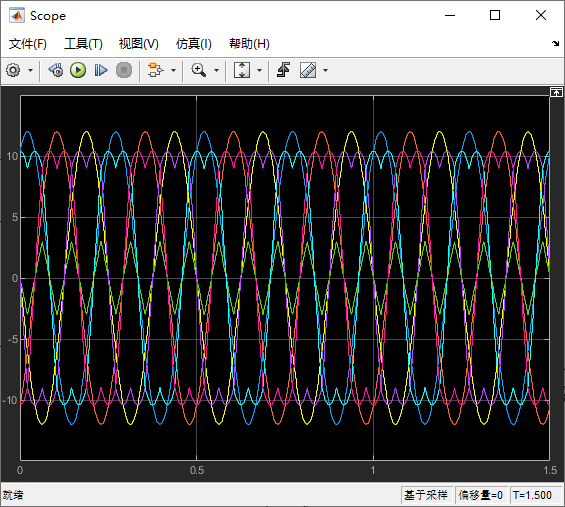
4.5.1 SPWM、SVPWM 和零序分量波形
这个波形包括 SPWM 和等价变换后的 SVPWM,可见在同等的输出效果中,SVPWM 要比 SPWM 的电压利用率要低。在 0 附近的三角波则是我们注入的零序分量。
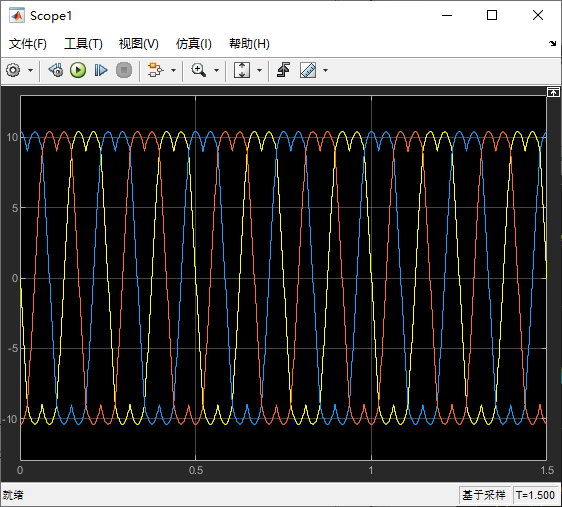
4.5.2 SVPWM 波形
4.5.3 除以母线的电压
最后我们将输出的 SVPWM 值除以母线电压后加 0.5,此时我们输出的电压范围 0~1。
五、电流环
3.1 电流环概述
电流环实际上是电机控制中的一个核心闭环,主要用于精确控制三相电机 (如 PMSM、BLDC) 的电流,使电机按期望转矩和磁场方向运行。
在 FOC 中,我们会把三相电流 、
、
通过 Clark 变换和 Park 变换,转到 d-q 坐标系,电流环就是 对 d、q 电流进行闭环控制,保证它们跟随给定的参考值的
、
。
3.2 电流环 PI 公式
3.3 仿真搭建
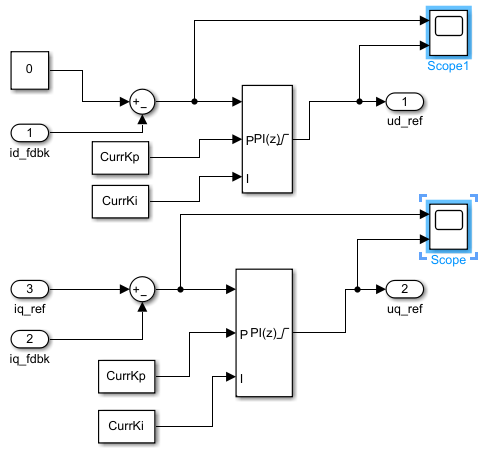
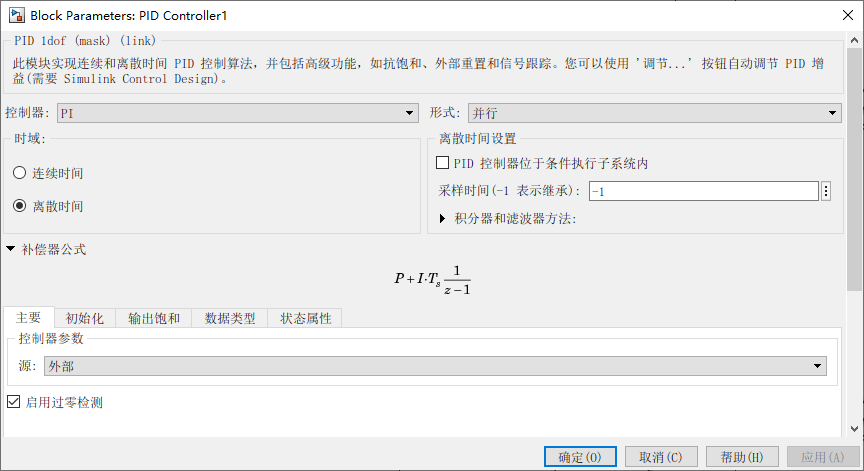
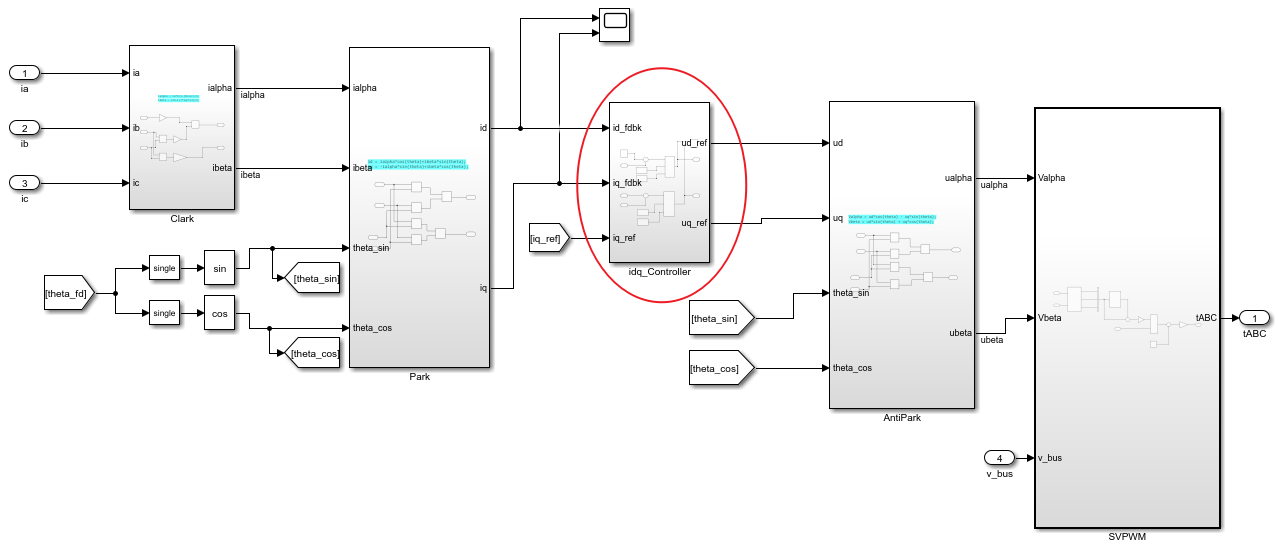
3.4 仿真结果
3.4.1 d 轴电流环 PI 调节
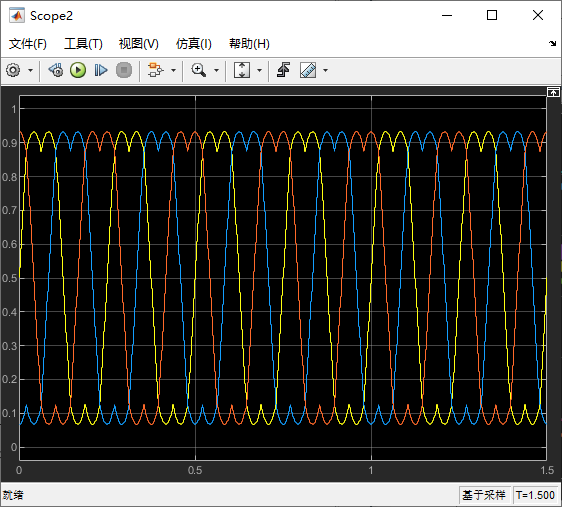
我们 d 轴的电流目标值为 0,其中黄线是 PI 输出值,蓝线是目标减去反馈的误差值。
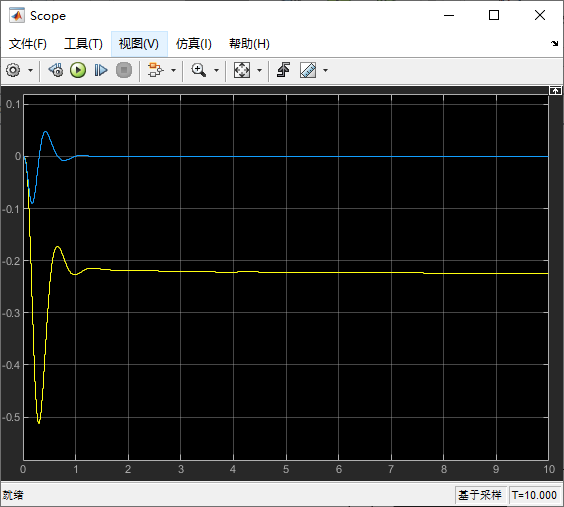
3.4.2 d 轴电流环 PI 调节
我们 d 轴的电流目标值为 5,其中黄线是 PI 输出值,蓝线是目标减去反馈的误差值。
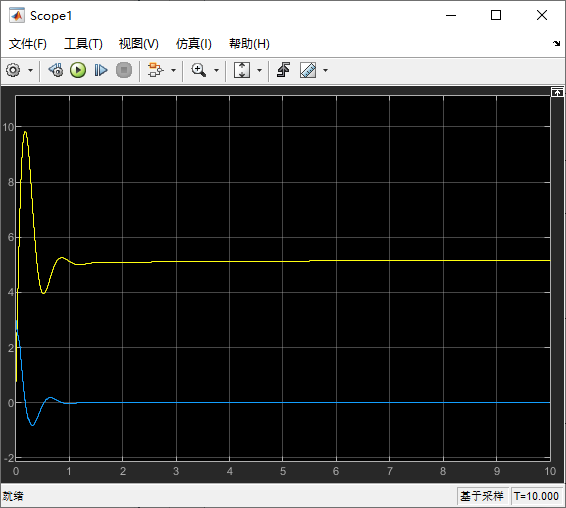
六、速度环
6.1 速度环概述
速度环是控制电机转速的外环控制器,位于:
位置环 → 速度环 → 电流环 → PWM/驱动。结构中,也是由速度环给目标电流,然后交给电流环做闭环运行。
FOC 中真正能让电机动起来的是电流环 (iq 控扭矩),而速度环的任务是根据转速误差决定应该给电流环多少 iq (扭矩) 指令。
6.2 仿真搭建
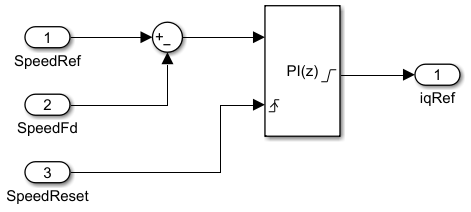
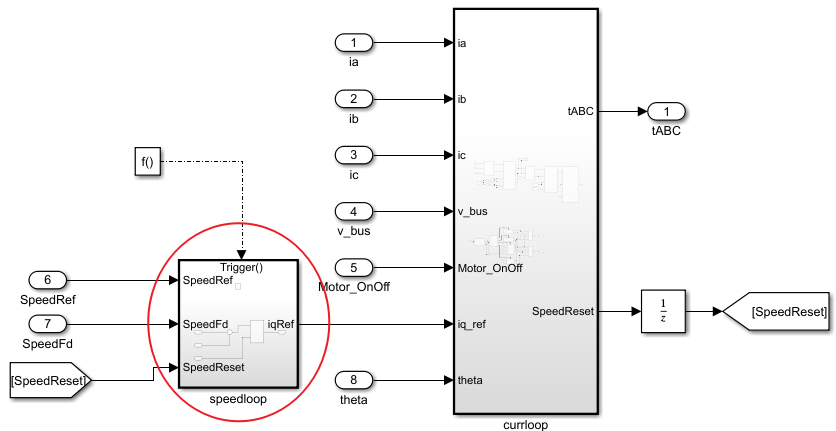























 5785
5785

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








