FOC 控制笔记【二】无感控制、滑膜观测器和 PLL

原创已于 2025-05-25 13:16:06 修改 · 2.4k 阅读

55 ·

CC 4.0 BY-SA版权

文章标签：

#笔记

于 2025-03-09 18:53:41 首次发布

电机笔记专栏收录该内容

10 篇文章

订阅专栏

一、无感控制基础

1.1 反电动势引入，电动机是不符合欧姆定律的电器

因为电机的定子由永磁铁构成，所以转子通电后受到会受到安培力的作用旋转。但是电机并不能简单的等效为一个电阻器。

假设：

电机内绕组铜丝是 1Ω；

我们供给 10V 的电压；

我们通常会发现电机仅消耗了 1A 左右的电流；

这样看起来并不符合欧姆定律。这是因为电动机转动时，线圈因切割磁感线，所以会产生感应电动势。线圈中产生的感应电动势跟加在线圈上的电压方向相反。

产生方式如下图所示，其中 R 和 L 被等效看作为电机的电气性质。

我们把这个跟外加电压方向相反的感应电动势叫做反电动势。

1.1.1 反电动势电路中的电压公式

$U = E+U_{R}$

$U$ = 供给电机的电压
$E$ = 反电动势的电压
$U_{R}$ = 电机自身的内阻所消耗的电压

1.1.2 电机线圈电流公式

线圈内电流为：

$I=\frac{U-E}{R}$

$E$ = 反电动势
$U$ = 外加电压
$R$ = 表示电动机回路总电阻

1.1.3 具有反电动势电路的功率关系

$IU-IE=I^2R$

$IU$ = 电源供给给电动机的功率（输入功率）
$IE$ = 电动机输出的机械功率
$I^2R$ = 热功损（铜损、铁损、机械损等）

1.1.4 根据安培力公式推算电机最大转速

安培力公式：

$E=BIv$

$B$ = 表示磁感应强度
$L$ = 表导体棒的长度
$v$ = 导体棒切割的速度

常理可知，电机反电动势不会大于供给的电压，加入我们给电机输入10V 电压，反电动势将不会超过 10V。

对于一个电机参数来说，B 和 L 是已知的，E 也不会超过输入电压，我们就可以根据这个公式推算出 v，进而得到电机空转的理论最大值。

二、推算转子角度与获得测量反向电动势

无感控制就是是从电机的反电动势中，获得当前电机转子的电角度。

2.1 电机的反电动势公式

根据电机反电动势公式：

$V_{BEMF} = -N\frac{\Delta (B\times A)}{\Delta t}$

$V_{BEMF}$ = 反电动势
$N$ = 线圈匝数
$B$ = 磁场的变化率 (T)
$A$ = 线圈截面积 ( $m^2$ )
$\Delta t$ = 产生磁场变化所经历的时间 (s)

通过这条公式，我们就能计算出电机再转动过程中，转子磁铁磁感线与线圈上的导线相互切割所产生的电压大小，这个电压的大小称之为反电动势。

无感控制的核心思路就是根据这个反电动势，来求出转子切割磁场的角度，也就是电角度。

2.2 反电动势和转子电角度的关系

BLDC 常采用集中整距绕组，反电势为梯形波，而 PMSM 多为分布短距绕组，反电势和电流均为正弦波。

下图中是 PMSM 电机的波形，但是随着近些年工艺提升，BLDC 的电机的反电动势也可以呈现正弦波。

下图中是

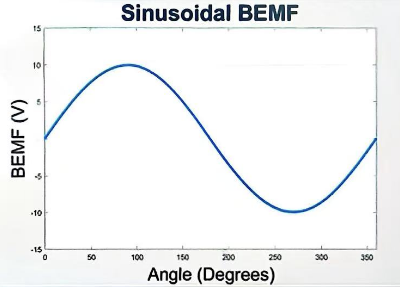
这张图是反电动势和转子电角度的关系，我们可知，反电动势其实是包含可转子的电角度信息的。

电机的反电动势公式也可以写成另一种和转子有关的写法：

$V_{BEMF} = \omega \times k_{e}\times sin(\theta + \varphi )$

$V_{BEMF}$ = 反电动势
$k_{e}$ = 被称为反电动势常数，单位 (mV/Hz)
$\theta$ = 无刷电机转子角度 (rad)
$\omega$ = 电机转速，单位 (Hz)
$\varphi$ = 相位差

在这个公式中的 $k_{e}$ 是由 $V_{BEMF} = -N\frac{\Delta (B\times A)}{\Delta t}$ 中的， $A$ = 线圈截面积 ( $m^2$ ) 和

$N$ = 线圈匝数得到的。

2.2.1 相位问题

由于电机三相角度相差为 120° ，A 相的反电动势，相位差为0°；B 相则是120°；C 相是240°。

也就是三项反电动势公式为：

$V_{BEMF_A} = \omega \times k_{e}\times sin(\theta + 0 )$

$V_{BEMF_B} = \omega \times k_{e}\times sin(\theta + 120 )$

$V_{BEMF_C} = \omega \times k_{e}\times sin(\theta + 240 )$

其中相位偏移图如下所示：

在得到任意两项的数据后，联立方程即可推算出电角度：

$\left\{\begin{matrix} V_{BEMF_A} = \omega \times k_{e}\times sin(\theta + 0 ) \\ V_{BEMF_B} = \omega \times k_{e}\times sin(\theta + 120 ) \end{matrix}\right.$

2.3 如何测量反电动势

2.3.1 电压平衡方程

如果我们将上图中 A 相位的反电动势看作为一个电池，其和电源电压是正极对正极，负级对负级的，也就是如下图：

根据基尔霍夫电压定律，电路中电压的合为 0 ，我们可以得到这个公式：

$0 = U_{a} - I_{m} \times R_{m} - L_{m} \times \frac{di_{a}}{dt} - V_{BEMF_{a}}$

$U_{a}$ = A 相的电压
$I_{m}$ = 当前相位的电流
$R_{m}$ = 电机内阻
$L_{m}$ = 电感的的值
$\frac{di_{a}}{dt}$ = 电流变化趋势微分
$I_{m} \times R_{m}$ = 电流乘电阻等于电压
$L_{m} \times \frac{di}{dt}$ = 电感所产生的电压，根据电感公式得到

其中电机的电压、内阻和电感的值都是已知的，电流可以通过电阻测量而出。

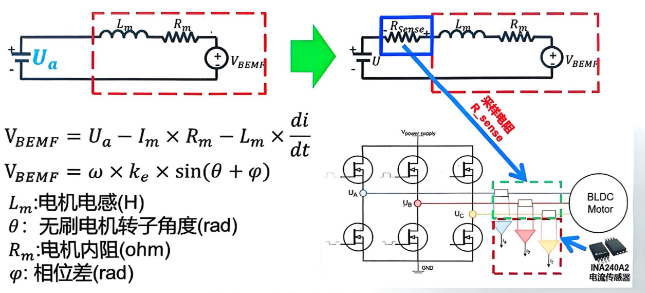
将计算得到的反电动势数据带入这个公式即可计算出电机的电角度。

$V_{BEMF} = \omega \times k_{e}\times sin(\theta + \varphi )$

三、反正切法求电机角度

2.1 单相反电动势方程

$0 = U_{a} - I_{m} \times R_{m} - L_{m} \times \frac{di_{a}}{dt} - V_{BEMF_{a}}$

$U_{a}$ = A 相的电压
$I_{m}$ = 当前相位的电流
$R_{m}$ = 电机内阻
$L_{m}$ = 电感的的值
$\frac{di_{a}}{dt}$ = 电流变化趋势微分
$I_{m} \times R_{m}$ = 电流乘电阻等于电压
$L_{m} \times \frac{di}{dt}$ = 电感所产生的电压，根据电感公式得到

继续取 A 相观察，再上一章中，根据基尔霍夫电压定律，电路中电压的合为 0 ，我们可以得到这个公式：

$U_{a} - I_{m} \times R_{m} - L_{m} \times \frac{di_a}{dt}-V_{BEMF_a} = 0$

通过移项可得：

$V_{BEMF_a} = U_{a} - I_{m} \times R_{m} - L_{m} \times \frac{di_{a}}{dt}$

提公因数可得：

$\frac{di_{a}}{dt} =-\frac{R}{L}i_{a}+\frac{1}{L_{m}}(U_{a}-V_{BEMF_a})$

至此，我们就得到了三项相反电动势方程：

$\frac{di_{a}}{dt} =-\frac{R}{L}i_{a}+\frac{1}{L_{m}}(U_{a}-V_{BEMF_a})$

$\frac{di_{b}}{dt} =-\frac{R}{L}i_{b}+\frac{1}{L_{m}}(U_{b}-V_{BEMF_b})$

$\frac{di_{c}}{dt} =-\frac{R}{L}i_{c}+\frac{1}{L_{m}}(U_{c}-V_{BEMF_c})$

其中，在左面的是都是电流的一阶导数。

2.2 电机电压方程的散点积分式

对电流变化趋势做积分，需要乘采样时间间隔 $T_{s}$ ，可以得到当前的电流：

$i_{a_{now}} = i_{a_{prev}}+\frac{di_{a}}{dt} T_{s}$

$i_{a_{prev}}$ = 上次计算的 $i_{a_{now}}$
$\frac{di_{a}}{dt}$ = 电流变化趋势微分

再结合电机电压方程可得散点积分式：

$i_{a_{now}} = i_{a_{prev}}+\frac{di_{a}}{dt}[-\frac{R}{L}i_{a}+\frac{1}{L_{m}}(U_{a}-V_{BEMF_a})]$

如果把经过 Clark 变换后的 α、β 也看成回路，可以类比为：

$i_{\alpha_{now} } = i_{\alpha_{prev} }+\frac{di_{\alpha }}{dt}[-\frac{R}{L}i_{\alpha }+\frac{1}{L_{m}}(U_{\alpha }-V_{BEMF_\alpha })]$

$i_{\beta_{now} } = i_{\beta_{prev} }+\frac{di_{\beta }}{dt}[-\frac{R}{L}i_{\beta }+\frac{1}{L_{m}}(U_{\beta }-V_{BEMF_\beta })]$

也可以成c语言的+=形式，进行积分：

$i_{\alpha} +=[-\frac{R}{L}i_{\alpha }+\frac{1}{L_{m}}(U_{\alpha }-V_{BEMF_\alpha })]$

$i_{\beta } += [-\frac{R}{L}i_{\beta }+\frac{1}{L_{m}}(U_{\beta }-V_{BEMF_\beta })]$

2.3 反正切求电角度

在散点积分式后，其中对于 $U_{\alpha }$ 、 $U_{\beta }$ 、 $i_{\alpha }$ 、 $i_{\beta }$ 都是已知值。

通过这些即可推算 $V_{BEMF_\alpha }$ 和 $V_{BEMF_\beta }$ 。

因为 α 轴和 β 轴呈 90°，所以使用反正切角度即可推算出电角度。

$\theta = -arctan(\frac{V_{BEMF_\alpha }}{V_{BEMF_\beta }})$

四、滑模观测器

根据相的反电动势公式计算并不是准确的：

$V_{BEMF_{a}} = U_{a} - I_{m} \times R_{m} - L_{m} \times \frac{di_{a}}{dt}$

其中，相电阻和相电感值依赖于电机运行的状态，如果稍有偏差，式子就不能正确的求出电机的反电动势。因为电机常是处于拖动、载荷运行等状态，所以电机发热会影响这些常数变化。这就导致最终通过反电动势计算的转子角度不准。

滑模观测器在做的是，把正确的反电动势看作一个滑模面：

先预估一个反电动势，然后根据公式反推出预估电流。将反推出的预估电流与真实电流差值做调整，最后加到反电动势上形成闭环。最后根据反正切函数计算出角度。

这种闭环允许电机内阻，电感等出现运动的动态的偏差。在上图中，滑模面是真实的反电动势，红色曲线则是预估的反电动势。

3.1 滑膜观测器的思路

以 A 相举例，滑膜观测器的思路是根据电压方程的散点积分式，先预测一个假定的 A 相反电动势，然后基于这个反电动势预测电流：

$i_{a_{now}} = i_{a_{prev}}+\frac{di_{a}}{dt}[-\frac{R}{L}i_{a}+\frac{1}{L_{m}}(U_{a}-V_{BEMF_a})]$

如果预测的电流等于真实测量的电流，那么反电动势也就是正确的：

$i_{a_{now}}$ (预测) - $i_{a_{now}}$ (真实) = 0

如果预测的电流不等于真实测量的电流，那么就是不对的：

$i_{a_{now}}$ (预测) - $i_{a_{now}}$ (真实) ≠ 0

到目前位置，滑膜观测器流程如下：

最后输出新的反电动势，应该根据预测结果正向调整反电动势：

$V_{BEMF_A} = h\times sign(i_{a_{-now}}($ 预测 $)-i_{a_{-now}}($ 真实 $))$

$h$ = 比例系数
$sat()$ = 限幅函数，将差值限定在某个范围内

如果只使用比较函数 sign 处理，会导致观测的滑模面跳动严重。

此时可以考虑使用 set 饱和函数：

$V_{BEMF_A} = h\times set(i_{a_{-now}}($ 预测 $)-i_{a_{-now}}($ 真实 $))$

$h$ = 比例系数
$sat()$ = 饱和函数，在输出时采用一段带有斜率的函数

3.2 滑膜观测器代码实现

根据我们之前的公式可知：

$\frac{di_{\alpha }}{dt} =-\frac{R}{L}i_{\alpha }+\frac{1}{L_{m}}(U_{a}-V_{BEMF_\alpha })$

我们需要上面的公式给等式右侧积分，这样可以得出估算电流，直接使用 C 语言的 += 形式给出：

$i_{\alpha} +=[-\frac{R}{L}i_{\alpha }+\frac{1}{L_{m}}(U_{\alpha }-V_{BEMF_\alpha })]$

//观察反电动势
Est_Ialpha += Ts * (-Rs / Ls * Est_Ialpha + 1 / Ls * (SMO_Ualpha - Ealpha));
Est_Ibeta += Ts * (-Rs / Ls * Est_Ibeta + 1 / Ls * (SMO_Ubeta - Ebeta));

//电流误差
float Ialpha_Err = Est_Ialpha - Ialpha;
float Ibeta_Err = Est_Ibeta - Ibeta;

//设计滑模面趋势律
Ealpha = h * sat(Ialpha_Err, 0.5f);
Ebeta = h * sat(Ibeta_Err, 0.5f);

//滑动滤波
Ealpha_flt = 0.1 * Ealpha_flt + 0.9 * Ealpha;
Ebeta_flt = 0.1 * Ebeta_flt + 0.9 * Ebeta;

//通过反正切发获得电机电角度
SMO_Est_theta = (-atan(Ealpha_flt / Ebeta_flt));

五、PLL 锁相环

通过对电机物理运动原理的理解，先把 error 类推为角加速度，对其求积分得到 $\theta$ 。

5.1 反电动势的帕克变换

这是帕克变换的变换公式：

$\begin{bmatrix} i_{d} \\ i_{q} \end{bmatrix} = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta &\cos\theta \end{bmatrix}\begin{bmatrix}i_{\alpha } \\ i_{\beta } \end{bmatrix}$

同样的，对于 d、q 轴的反电动势来说，可以进行帕克变换：

$\begin{bmatrix} E_{d} \\ E_{q} \end{bmatrix} = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta &\cos\theta \end{bmatrix}\begin{bmatrix}E_{\alpha } \\ E_{\beta } \end{bmatrix}$

5.2 d 轴反电动势为 0 的估算

只提出 d 轴，可得：

$E_{d} = E_{a}\cos\theta+E_{\beta }\sin\theta$

在 d 轴电流为 0 的情况，此时 d 轴的反电动势也应为 0：

$E_{d} = E_{a}\cos\theta+E_{\beta }\sin\theta = 0$

那么，预估的反电动势 $E_{d_{est}}$ 也应该等于 0：

$E_{d_{est}} = E_{a}\cos\theta_{est}+E_{\beta }\sin\theta_{est} = 0$

如果 $\theta_{est}$ 角度不准确，也就是预估的 $E_{d_{est}}$ 不等于 0：

$E_{d_{est}} = E_{a}\cos\theta_{est}+E_{\beta }\sin\theta_{est} \neq 0$

5.3 计算电角度误差

此时可以先计算出电角度误差值。

在电机加速度时，由于传感器通常是测得电流值后，再计算观测的电角度 $\theta_{est}$ 的，当计算加速度时，总会滞后真实的 $\theta$ ，当电机加速或减速时，这个 error 的偏差值就会一直存在。

电机反电动势的大小与电机的电磁力直接相关，电机的电磁力又与电机的转子加速度相关联。因此，电机的反电动势，其实是和转子的加速度存在等效关系。

所以根据以上推理，error 和加速度呈正向关系：

$error=E_{d} - E_{d_{est}}$

由于实际物理系统中被设定为 $E_{d}$ 等于 0，就可以合并式子：

$error=E_{d} - E_{d_{est}}=0-(E_{a} \cos\theta_{est} + E_{\beta }\sin\theta_{est})$

5.4 求转子加速度

此时， $error$ 可以看作为电机转子加速度， $Ki$ 则是加速度系数(根据实际情况调节)，对他求积分得转子速度：

$i_{err} = \sum T_{s}\times K_{i}\times error$

在下列式子中， $K_{p}\times error$ 的目的是提升 $\theta$ 点的输出响应，因为 mcu 的计算累加积分需要时间，这样可以加重瞬时加速度输出的权重，最终，得到一个高质量的转子速度值：

$\theta = K_{p}\times error+i_{err}$

5.5 低通滤波

5.6 积分得角度

5.7总结

5.8 PLL 锁相环流程图

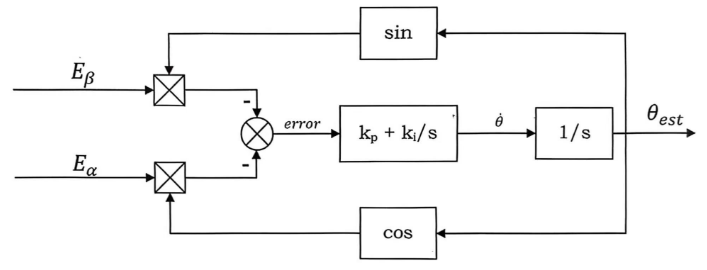
滑模观测器与 PLL 观测器的关系：

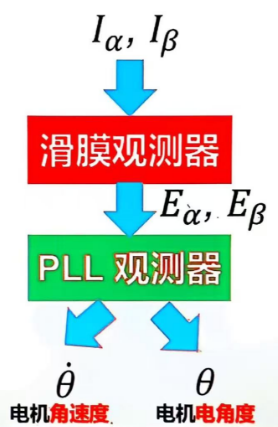
5.2 PLL代码演示

//求电角度差值
float Theta_err = -1 * alpha * cos(Est_Theta) + beta * sin(Est_Theta) * -1;
//求转子速度
i_err += Ts * PLL_ki * Theta_err;
Est_speed = PLL_kp * Theta_err + i_err;
//低通滤波
Est_speed_F = Est_speed_F * 0.96 + Est_speed * 0.04;
//速度积分得电角度
Est_Theta += Ts *  Est_speed_F ;  // 对电角速度进行积分获得电角度