岭回归与LASSO回归：解析两大经典线性回归方法

🍋引言

在机器学习和统计建模中，回归分析是一项重要的任务，用于预测一个或多个因变量与一个或多个自变量之间的关系。在这个领域中，有许多回归方法可供选择，其中岭回归和LASSO回归是两种经典的线性回归技术。在本文中，我们将深入探讨这两种方法的原理、应用和优缺点，帮助您更好地理解它们在实际问题中的作用。

前些天发现了一个巨牛的人工智能学习网站，或许可以对学习机器学习的小伙伴有一定的帮助，分享一下给大家。感兴趣的同学可以看看，点击链接

🍋岭回归（Ridge Regression）

岭回归，又称L2正则化，是一种用于解决多重共线性问题的线性回归技术。多重共线性是指自变量之间存在高度相关性的情况，这会导致普通最小二乘法（OLS）估计的不稳定性，使得模型的预测性能下降。岭回归通过在损失函数中添加一个正则化项来解决这个问题，其数学表达式如下：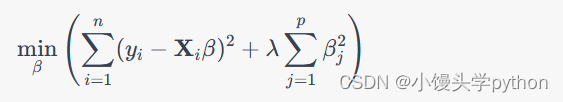

其中，$y_i$ 是观测值，${\mathbf{X}}_i$ 是自变量矩阵，$\beta$ 是待估计的回归系数，$\lambda$ 是正则化参数，用于控制正则化的强度。岭回归通过增加${\beta }_j$的平方和来限制回归系数的大小，从而减少多重共线性对估计结果的影响。

岭回归的优点包括：

• 改善多重共线性问题。
• 稳定的估计结果，不容易受到异常值的影响。
• 可以处理高维数据集，避免过拟合。

然而，岭回归也有一些缺点，例如它不能自动选择重要的特征，需要手动调整正则化参数$\lambda$，并且可能不适用于稀疏数据集。

🍋实战—岭回归

首先我们假设一组数据

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = np.random.uniform(-3,3,size=