DPO（Direct Preference Optimization）原理和代码实战

一、前言

RLHF中的PPO算法存在以下问题：

• 流程复杂： 需要构建一个反映人类偏好的奖励模型
• 训练不稳定：引入多个模型包括：reward model、critic model、actor model、ref_actor model

而 DPO 本身是一种不需要强化学习的算法，简化了整个 RLHF 流程，训练起来会更简单。

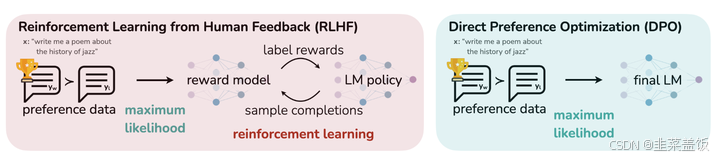
DPO 省略了reward model、critic model两个模块，直接优化目标模型（Actor）的参数，使其生成更符合人类偏好的输出。简而言之，DPO 不依赖强化学习中的“奖励”机制和“批评”机制，而是通过人类反馈直接指导优化过程。

二、DPO公式解释

这里先放一下DPO最终的公式
$${\mathcal{L}}_{\text{DPO}}({\pi }_{\theta };{\pi }_{\text{ref}})=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\ln \sigma \left(\beta \ln \frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\text{ref}}(y_w\mid x)}-\beta \ln \frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{\text{ref}}(y_l\mid x)}\right)\right]$$

${\mathcal{L}}_{\text{DPO}}({\pi }_{\theta };{\pi }_{\text{ref}})\text{是 DPO 算法的损失函数，表示用于优化模型参数}\theta \text{的目标函数。}$

${\pi }_{\theta }\text{是当前要训练的模型，其参数为}\theta \text{，用于生成文本。}$

${\pi }_{\text{ref}}\text{是参考模型，即}{\pi }_{\theta }\text{的备份（不再更新），用于训练稳定}$

$\mathcal{D}\text{是数据集，包含了输入}x\text{和对应的合理文本}{y}_w\text{和不合理文本}{y}_l\text{。}$

$(x,y_w,y_l)\text{是数据集中的一个样本，其中}x\text{是输入文本，}{y}_w\text{是生成的合理文本，}{y}_l\text{是生成的不合理文本。}$

$\sigma \text{是 sigmoid 函数，将输入值映射到}[0,1]\text{。}$

$\beta \text{是一个超参数，用于控制损失函数中不合理文本相对于合理文本的权重。}$

$\frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\text{ref}}(y_w\mid x)}\text{确保生成的文本在一定程度上与参考模型保持一致，防止训练偏了。}$

对公式进一步推导：
$$\begin{gathered} L_{\text{DPO}}({\pi }_{\theta };{\pi }_{\text{ref}})=-{\mathbb{E}}_{\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }(y_w)}{{\pi }_{\text{ref}}(y_w)}-\beta \log \frac{{\pi }_{\theta }(y_l)}{{\pi }_{\text{ref}}(y_l)}\right)\right] \\ =-{\mathbb{E}}_{\sim \mathcal{D}}\left[\log \sigma \left(\beta \left(\log \frac{{\pi }_{\theta }(y_w)}{{\pi }_{\text{ref}}(y_w)}-\log \frac{{\pi }_{\theta }(y_l)}{{\pi }_{\text{ref}}(y_l)}\right)\right)\right] \\ =-{\mathbb{E}}_{\sim \mathcal{D}}\left[\log \sigma \left(\beta \left((\log {\pi }_{\theta }(y_w)-\log {\pi }_{\text{ref}}(y_w))-(\log {\pi }_{\theta }(y_l)-\log {\pi }_{\text{ref}}(y_l))\right)\right)\right] \\ =-{\mathbb{E}}_{\sim \mathcal{D}}\left[\log \sigma \left(\beta \left((\log {\pi }_{\theta }(y_w)-\log {\pi }_{\theta }(y_l))-(\log {\pi }_{\text{ref}}(y_w)-\log {\pi }_{\text{ref}}(y_l))\right)\right)\right] \\ \text{其中 }\pi (y)=\pi (y\mid x) \end{gathered}$$

其中
$pi\_logratios=\log ({\pi }_{\theta }(y_w))-$