Dijkstra算法——基本原理 + 各部分本质及其衍生操作

Dijkstra背景

Dijkstra是研究

1. 单源
2. 最短
3. 路径长度

的算法
且 边长度/权值 不能有负数

注：且大部分题目都以无向边形式呈现

Dijkstra原理解析

Dijkstra的思路是更新2个表，其中有

1.  mark：标记点是否被访问过
2.  path：走到每个点的权值/路径
3.  其他追加记录：可访问表（略）

写法上

Dijkstra有3个模块；

模块0：设定初始状态
1、visit设定全false 2、path设定全为INT_MAX，起始点为0 3、定义 每次访问的点；最小路经

开始循环：设定最小路经为 INT_MAX

1. 模块1——循环1：遍历visit表；找到path表中最小的 点；
2. 模块2：更新visit表及其他操作（例如 记录访问的点 等）
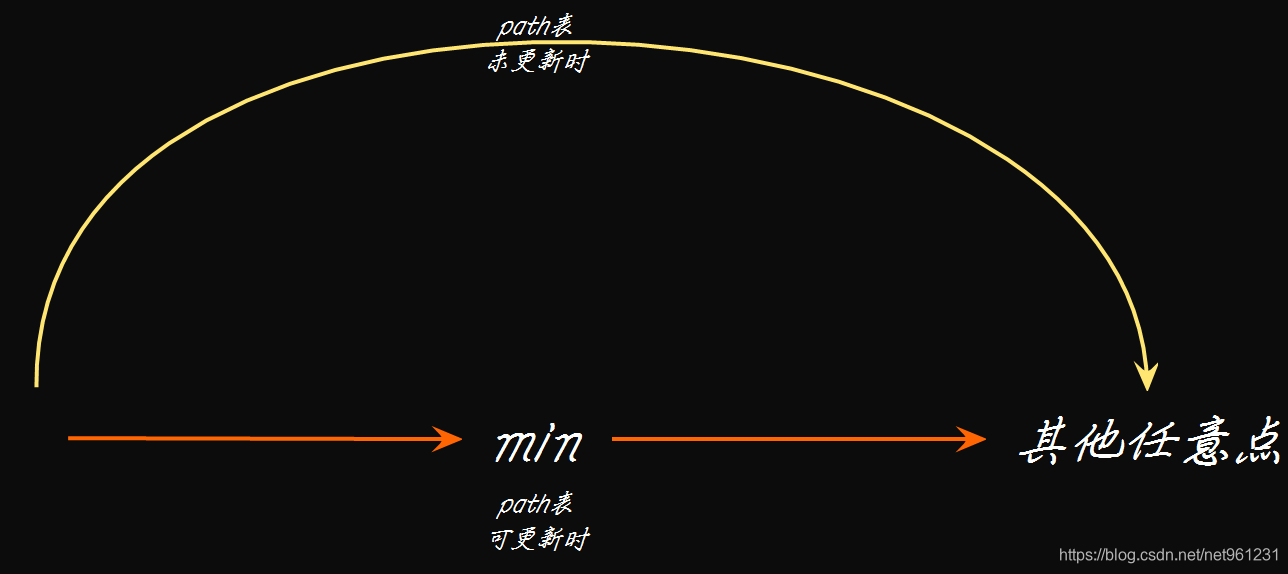
3. 模块3——循环2：遍历min的邻接点；更新path表

原因：当走到min点后，可不可能存在：“通过先到min，再到目标点 比 原来直接达到目标点 更短”
若有则更新path表

模块1的追加操作：强化贪心判断（存在先后优先级的多个判断）

操作1的本质：Dijkstra的核心思想——贪心（每次都抓取局部最优解）

操作1：追加点权——要求在同时最短路下，同时判别点权最小/大

for (auto i = visit.begin(); i != visit.end(); ++i) {
	if (i->second == false && length[i->first] < min_path) {
		min_path = length[i->first];
		next = i->first;
	}
	else if (i->second == false && length[i->first] == min_path) {
		if (happy_sum[i->first] > happy_sum[next]) {
			next = i->first;
		}

在操作1的基础上可以进行拓展，追加多个判断

 

模块2的追加操作：

模块2的本质：在Dijkstra的已找到最优解下，进行记录
即：全局操作

 

模块3的追加操作：拓展处理双源问题（明确起点和终点）

模块3的本质：当有点可访问时/存在更短的路经时；更新对这个点的一系列状态（所需路经等）
即：局部操作

注：以上操作仍然要全部点访问一遍再跳出Dijkstra，即做一次完整的Dijkstra
而不是访问到终点就跳出

操作1：确定1条双源最短路经

原理：用1个容器，来记录前后关系

具体操作：

初始化：对每个点，与他自身进行线索

例：输入时作如下操作

tree[x] = x;

实际过程类似构建1个以起点为根的n叉树

在模块3的循环下添加：(此处以邻接表为例)

for (auto i = graph[u].begin(); i != graph[u].end(); ++i) {
	if (visit[(*i).v] == false && (*i).key + length[u] < length[(*i).v]) {
		length[(*i).v] = (*i).key + length[u];
		tree[(*i).v] = next;//每次有更小路经时，则挂上前驱
	}
}

最终脱出Dijkstra时，从想要的终点进行逆向线索到起点即可

操作2：确定双源最短路经的条数

原理：用1个容器，来记录访问到该结点的路经数

具体操作：

初始化：对起点start，设置cout[start]=1

在模块3的循环判断 下添加：

在＜时追加

path_number[(*i).v] = path_number[u];

在==时追加

path_number[(*i).v] += path_number[u];

课后练习

PAT 1087 All Roads Lead to Rome

此题网上大部分解都是基于柳神的DFS+Dijkstra

但是可以只用Dijkstra进行破解，考察了贪心法的思路和对点的维护
即 模块1和模块3的追加操作

注：用柳神的办法确实好理解，但是如果能用纯Dijkstra进行破解，定能加深你对Dijkstra本质的理解

注：以上全文都是基于该题，产生的新理解，新总结