路由寻迹常见算法-启发式

路由寻迹之启发式搜索

启发式搜索是指我们在搜索路径时，首先选择最有希望的的节点去拓展，这种被称为启发式搜索.

启发函数

那么什么可以用来定义最有希望，如何来界定一个点比另外一个点、一个网格比另外一个网络更有希望，这就要通过启发函数来进行计算得到。
对于我们常见的网格图来说，我们规定只能上下左右来移动的话，那么通常来说都会使用曼哈顿距离来当做启发函数。

什么是曼哈顿距离

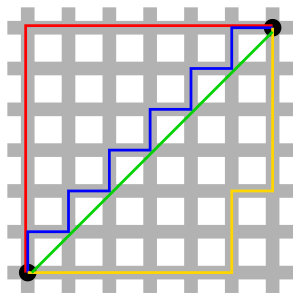
根据官方定义，曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj. |+|yi-yj. 。 对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。

function Manhattan(node) =
    dx = abs(node.x - g