基于距离的蓝牙定位方式介绍

室内定位小白

已于 2025-03-13 19:50:39 修改

阅读量652

点赞数 6

CC 4.0 BY-SA版权

分类专栏：室内定位及涉及算法文章标签：算法

于 2025-03-06 20:28:33 首次发布

本文链接：https://blog.youkuaiyun.com/navsense_support/article/details/146079336

室内定位及涉及算法专栏收录该内容

6 篇文章

订阅专栏

一、三边定位：基础原理

三边定位是一种常见的定位方法，广泛应用于无线通信、GPS、蓝牙等技术中。其基本原理是通过测量目标设备与多个已知位置的信标之间的距离，结合几何推导来估算设备的位置。

1. 三边定位的基本思想

假设有三个已知信标，它们的位置分别为 (x1,y1)，(x2,y2)(x2,y2)，(x3,y3)(x3,y3)，同时，测得目标设备与这三个信标的距离分别为 d1，d2，d3。在理想情况下，通过以下几何方法，设备的位置 (x,y) 会落在三个信标圆的交点上。

对于每个信标，设备到信标的距离可以表示为一个圆的方程：

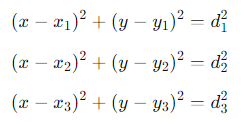
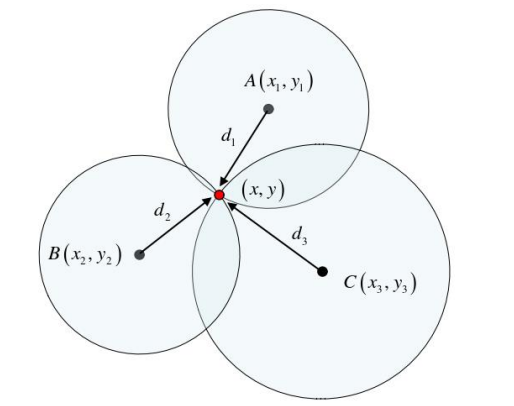
通过解这三个方程，可以求出设备的坐标 (x,y)。

2. 问题与挑战

测量误差： 在实际应用中，由于环境干扰、设备精度限制、信号多径效应等因素，测得的距离往往存在误差。
几何问题： 三个信标的测量距离并不总是能够精确地交于一个点，特别是在多径效应和信号干扰严重的环境中，信号的测量误差会导致定位误差。

尽管如此，三边定位方法仍然在许多应用中被广泛使用，尤其是当信号干扰较小、测量精度较高时。

二、基于最小二乘法的三边定位：优化定位精度

由于传统的三边定位方法存在测量误差，且无法完全消除误差，基于最小二乘法的三边定位应运而生。最小二乘法是一种通过优化误差平方和来求解问题的方法，广泛应用于数据拟合和优化问题。

1. 最小二乘法的基本概念

最小二乘法的基本思想是：在面对不确定性和噪声的情况下，我们通过最小化所有误差的平方和，得到最优的解决方案。在三边定位中，误差是指设备的估计位置与测量的距离之间的差异。

对于三边定位问题，最小二乘法的目标是：最小化每个信标位置到设备位置的预测距离与实际测量距离之间的误差。

2. 最小二乘法如何优化三边定位

假设目标设备与三个信标之间的测量距离分别为 , , , 并且信标位置为 , , , 我们可以通过以下方式计算误差:

对于第一个信标, 误差为:

对于第二个信标, 误差为:

对于第三个信标, 误差为:

最小二乘法的目标是最小化误差的平方和:

通过调整设备位置 (x,y)，使得所有信标的距离误差最小，最小二乘法会找到一个优化后的设备位置。

3. 通过最小二乘法计算定位

在实际应用中，最小二乘法通过迭代的方式不断调整设备的位置，直到所有信标的距离误差的平方和最小。这种方法可以有效地改善测量误差带来的定位精度问题，特别适用于实际环境中的多信标定位系统。

常用的优化算法包括 高斯-牛顿法（Gauss-Newton） 和 列文伯格-马夸尔特法（Levenberg-Marquardt），这些方法能在迭代过程中快速收敛并找到最佳解。

三、代码实现与三边定位

以下是基于最小二乘法的三边定位代码实现。我们从三个信标位置与测量的距离出发，使用最小二乘法求解设备位置。

import numpy as np
from scipy.optimize import least_squares

# 信标位置（统一使用冒号分隔的格式）
beacon_positions = {
    "A4:9E:69:95:1E:3B": (0, 0),
    "BC:02:6E:9C:66:28": (0, 2),
    "BC:02:6E:9C:68:52": (0, 4),
}

# 通过 RSSI 计算距离的函数
def rssi_to_distance(rssi, tx_power=-80, n=4):
    return 10 ** ((tx_power - rssi) / (10 * n))

# 最小二乘法的残差函数
def residuals(p, beacons, distances):
    x, y = p
    return [np.sqrt((x - bx)**2 + (y - by)**2) - d 
            for (bx, by), d in zip(beacons, distances)]

# 三边定位的主函数
def trilateration(beacons, distances):
    result = least_squares(residuals, [0, 0], args=(list(beacons.values()), distances))
    return result.x if result.success else (None, None)

# 测试数据（假设我们从信标和测量的 RSSI 值计算得到了距离）
distances = [5.0, 5.2, 6.1]  # 假设的距离数据（单位：米）

# 进行定位
estimated_position = trilateration(beacon_positions, distances)
print(f"估计的位置是: X = {estimated_position[0]:.2f}, Y = {estimated_position[1]:.2f}")