逻辑回归（Logistic Regression）

1.推导

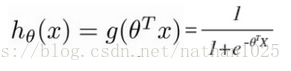      sigmoid函数

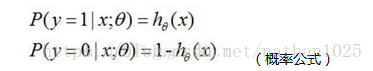
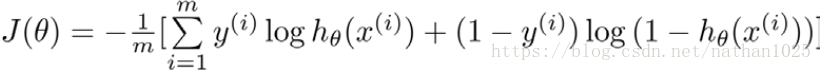
2式可以简化为

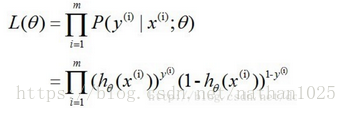
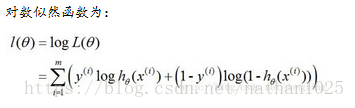
使用梯度下降法求J(θ)的最小值，θ的更新过程：

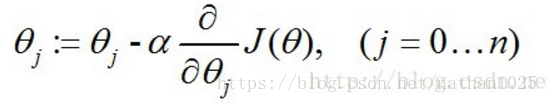
    for k in range(maxCycles):              #heavy on matrix operations

        h = sigmoid(dataMatrix*weights)  

        error = (labelMat - h)              #vector subtraction

        weights = weights + alpha * dataMatrix.transpose()* error

    return weights

3.改进

    for j in range(numIter):

        dataIndex = range(m)

        for i in range(m):

            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not

            randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant

            h = sigmoid(sum(dataMatrix[randIndex]*weights))

            error = classLabels[randIndex] - h

            weights = weights + alpha * error * mat(dataMatrix[randIndex]).transpose()

            del(dataIndex[randIndex])//？不放回

 

http://blog.jobbole.com/113182/

https://www.cnblogs.com/alfred2017/p/6627824.html