高效算法，B*寻路算法，python版，思维优化（2）

原创已于 2022-05-01 14:49:58 修改 · 2.1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #python #开发语言

于 2022-04-29 14:34:58 首次发布

接着上一篇，我们继续讲解B*寻路算法，上一段的代码段，这节我们说一下方向向量，下一节我们对得到的路劲进行进一步优化，最终版的话，下面这段代码其实是没用的，根本不需要沿着障碍爬，但是基础的还是要一步步讲解的

# 返回爬墙路径 和 直线穿透障碍的第一个点,,    传入的是 当前点 {}字典信息  和 前进一步的障碍点坐标元祖  （）
#  点信息 为  {"point"：（坐标），”direct“：（指向自己的向量（元祖）），其他自定义信息 }
def obstacle_path(self, cur, obstacle_point: tuple):
    # 障碍前的点
    temp_point = cur["point"]
    # 获取指向终点的向量
    direct=self.get_direct(temp_point)
    while True:
        # 传进来的点,沿着终点方向，穿透障碍，得到可以探索的第一个点     ：地图内的任意两点连线都不可能穿过地图边界
        end_point = temp_point[0] + direct[0], temp_point[1] + direct[1]
        if map_be_search[end_point[0]][end_point[1]] == 0:
            break
        temp_point = end_point
    end_info = {}
    end_info["point"] = end_point
    # end_info  的direct 需要攀爬过后才能知道
    #--------穿透后的点已经好了


    # 开始爬墙，先 把障碍周围所有可走的点拿到    为obstacle_path
    obstacle_path=self.get_obstacle_path(obstacle_point)
    # ----------------第一轮 攀爬-----------
    # 这里是零时的 关闭表 ，实际上这里应该的全局关闭表
    closeSet=[]
    cur_grid = cur  # 把传进来的那个点拿来用
    while True:
        closeSet.append(cur_grid)
        # map_be_search[cur["point"][0]][cur["point"][1]] = 5
        # print(map_be_search)
        # time.sleep(0.5)

        # 当前点已经是 穿透后的点了， ！！！这里终点已经加入了closeSet 后面有用 !!
        if cur_grid["point"] == end_point:
            break

        # 对当前格相邻的8格中的每一个
        neighbors = self.get_neighbors(cur_grid["point"][0], cur_grid["point"][1])
        next_point_info = {}
        for neighbor in neighbors:
            #  该邻居 在障碍周围的可探索点中。 并且没有关闭（走过），则下一个点就是它
            if neighbor in obstacle_path and neighbor not in closeSet:
                # 计算距离  ==1.4 的是对角的点
                distace=self.get_distance(cur_grid["point"],neighbor)
                if distace==1:
                    next_point_info["point"] = neighbor

                    # 这里记录的的父节点指向自己的向量，也可以改为“parent”:cur["point"]，只是用来回溯路劲的
                    next_point_info["direct"] = self.get_two_point_direct(cur_grid["point"], neighbor)
                    # 但是对于最初的一个点来说，它的邻居 左右（前进方向）有两个点是符合的，这里打断一下只取一个。所以第二轮的攀爬，虽然是同一个起点，但是却取了另一个分支
                    break

        # 沿着障碍边缘走，前路 要么有且只有一个点可走，要么死路,要么已经到达了穿透后的点
        if next_point_info:
            cur_grid=next_point_info
        else:
            break

    # -------- 到这里，closeSet记录的是第一条路径的所有点 ----第二轮攀爬   其实就是重复一下 刚好的是初始点的另一个分支--------------
    length1 = len(closeSet)
    cur_grid = cur  # 把传进来的那个点拿来用,用过就关闭，无情
    while True:
        closeSet.append(cur_grid)

        # map_be_search[cur["point"][0]][cur["point"][1]] = 5
        # print(map_be_search)
        # time.sleep(0.5)

        # 当前点已经是 穿透后的点了，
        if cur_grid["point"] == end_point:
            break

        # 对当前格相邻的8格中的每一个
        neighbors = self.get_neighbors(cur_grid["point"][0], cur_grid["point"][1])
        next_point_info = {}
        for neighbor in neighbors:
            #  该邻居 在障碍周围的可探索点中。 并且没有关闭（走过），则下一个点就是它
            if neighbor in obstacle_path and neighbor not in closeSet:
                # 计算距离  ==1.4 的是对角的点
                distace = self.get_distance(cur["point"], neighbor)
                if distace == 1:
                    next_point_info["point"] = neighbor
                    next_point_info["direct"] = self.get_two_point_direct(cur_grid["point"],neighbor)  # 这里记录的的父节点指向自己的向量，也可以改为“parent”:cur["point"]
                    # 但是对于最初的一个点来说，它的邻居 左右（前进方向）有两个点是符合的，这里打断一下只取一个。所以第二轮的攀爬，虽然是同一个起点，但是却取了另一个分支
                    break

        # 沿着障碍边缘走，前路 要么有且只有一个点可走，要么死路
        if next_point_info:
            cur_grid = next_point_info
        else:
            break



    # ，，如果只有一条路径到达，那么探索过 end_point点只有一个，否则有两个相同的 end_point，但是他们的父节点不一样，回溯路径是不好处理，
    lenght2 = len(closeSet)

                #  遍历 closeSet  如果坐标点=终点坐标，就拿出它对应的索引
    last_index = [closeSet.index(p) for p in closeSet if p["point"] == end_point]
    # 为空，两条都死路，，也就是坑爹的 空心障碍，，或者目标终点在里面，一样坑爹
    if last_index == []:
        return 0
    else:
        # 有一个就是有一条路，直接返回回就行
        if len(last_index) == 1:
            return closeSet[last_index[0]]

        # ----通过两轮攀爬的 路径长度，， 舍去其中一个 end_point,留下一个即可,不然回溯路劲时，一个点有两个指向自己的向量（两个父节点）
        if length1< (lenght2-length1):
            closeSet.pop(last_index[1])
            return closeSet[last_index[0]]
        else:
            closeSet.pop(last_index[0])
            return closeSet[last_index[1]]

方向向量：就是两点之间的指向（高中的知识把）我们先考虑四个方向，也就是，只能朝着四个方向移动

（B*算法是直线穿透，所以要考虑八个方向）

由斜率来得到. 红点：起点（1,1）终点：（-1,-2），斜率k=3/2,>1 说明是比较偏y轴的，所以考虑（0,1）和（0，-1）

但是x_sub= -1-1 小于0，向量指向在y轴左边所以返回（0,-1）

该点下一步就是加上该方向向量就能等得到下一点的坐标例如（0,0）>(1,1),有0，0指向1，1的向量就是（1,1,）

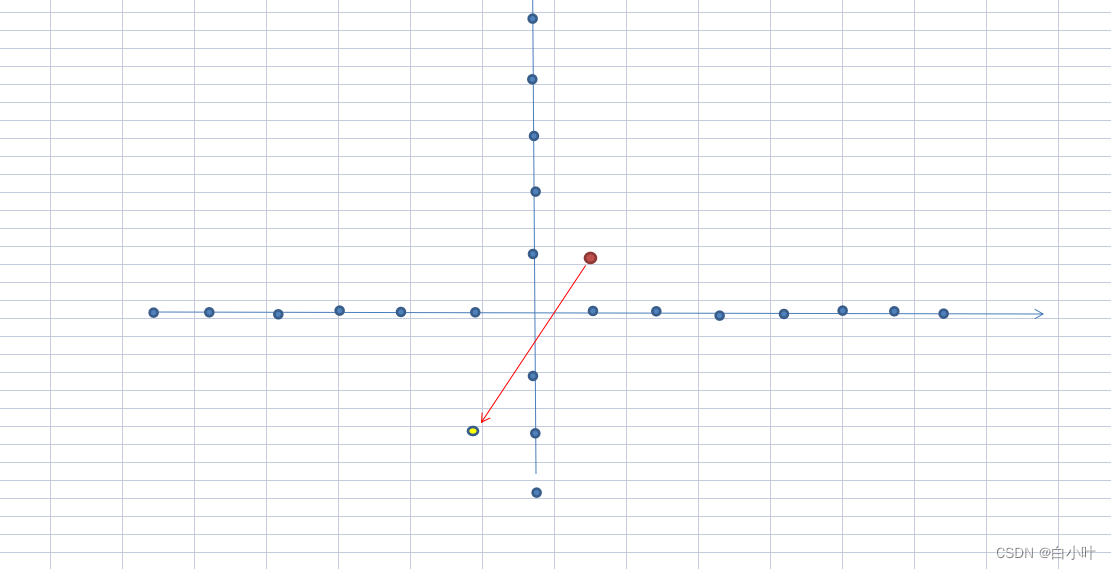
具体判定：返回的是单位向量，因为每步走一格

-1<斜率<1 偏向x 轴就考虑（1,0）和（-1,0），x_sub>0 就（1,0），x_sub<0 就（-1,0）注：指向终点的线可以看做长向量，和单位向量（1,0）和（-1,0）相比，因为偏向x轴，就不用看 y_sub, x_sub为正就指向正（1,0）

2. -1>斜率 and 斜率 > 1 偏向Y轴 y_sub>0 就（0,1），y_sub<0 就（0-1）。。边界值-1/2 和1/2，随便就好了

特殊情况指向线在 x 轴上。这时候斜率为 0 ，并入上面的就行

特殊情况指向线在 Y轴上。x_sub= 0 y_sub= +-？，斜率都没有算个锤子，因为0 不能作为被除数,直接返回（0，y_sub/abs(y_sub)）

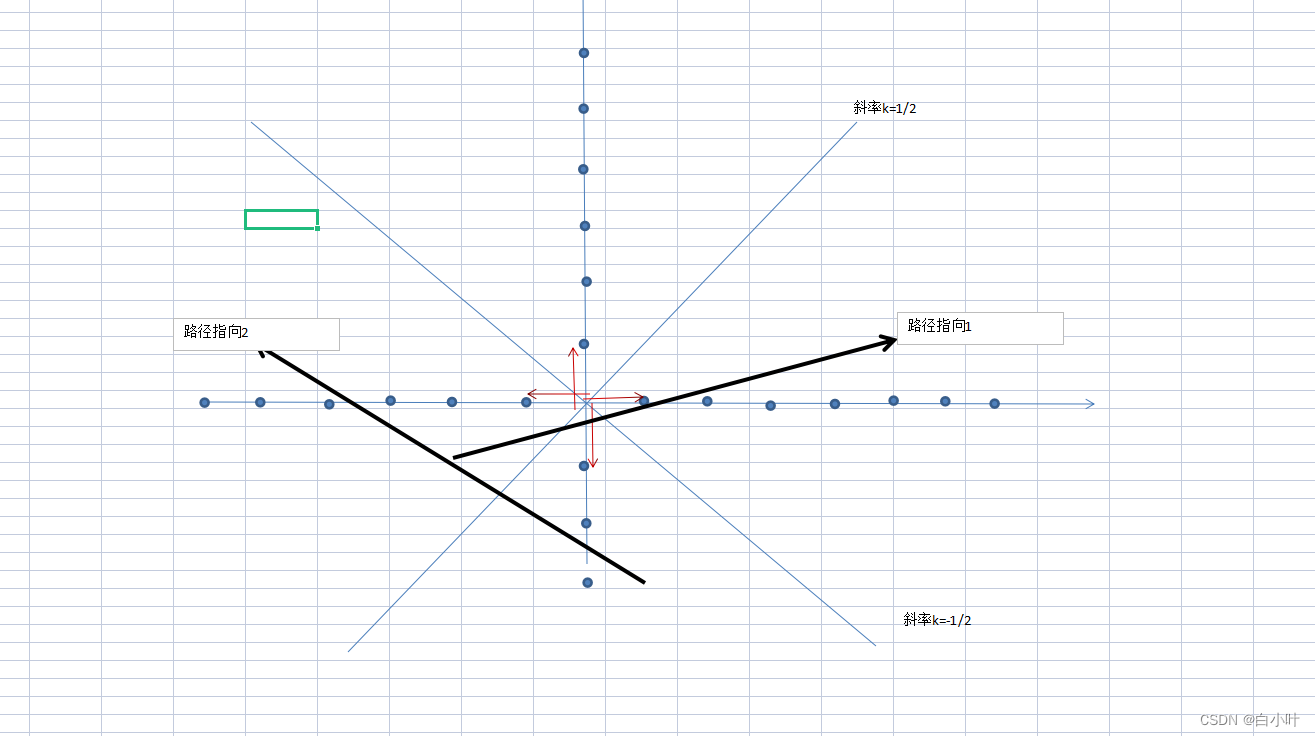
通过不断的获取指向目标终点的方向向量，一直加就能到达目标终点

    # 当前点指向终点的向量。  四个方向  通过斜率相近 得到方向向量（1,0），（-1,0）（0，-1）（0,1）
    def get_direct(self, cur):
        x_sub, y_sub = (self.end["point"][0] - cur[0]), (self.end["point"][1] - cur[1])
        # 说明 垂直 x轴上， k = y_sub / x_sub  0为被除数
        if x_sub == 0:
            # 可能是 除以绝对值
            return x_sub, y_sub / abs(y_sub)
        # 计算斜率
        k = y_sub / x_sub
        if -1 <= k <= 1 :
            if x_sub < 0:
                return (-1, 0)
            else:
                return (1, 0)
        if k<(-1) and k>1 ：
            if y_sub > 0:
                return (0, 1)
            else:
                return (0,-1)

接下来考虑八个方向其原理也是一样的。只不过斜率切分成了几段

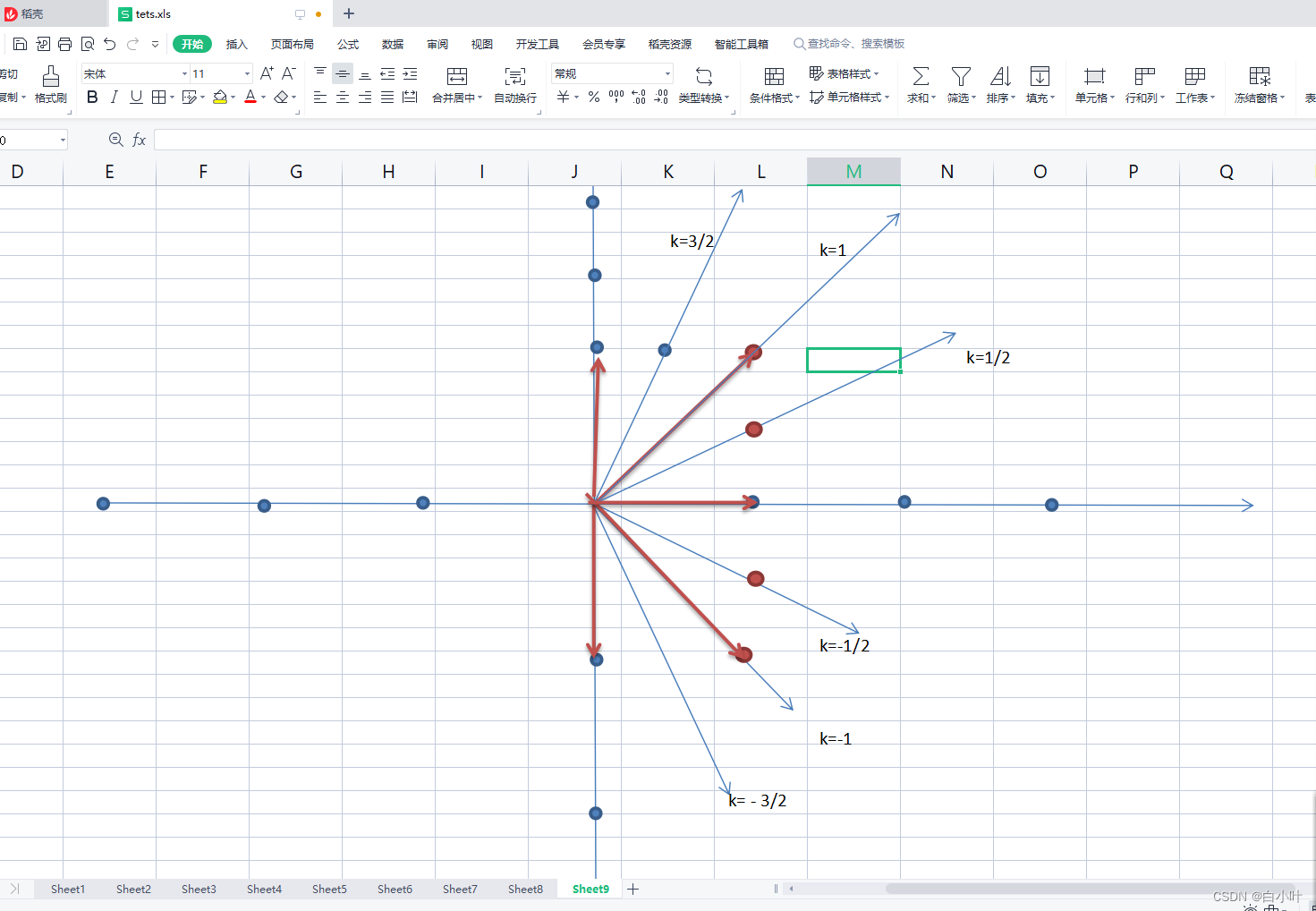
    # 当前点指向终点的向量。 八方向  通过斜率相近得到方向向量（1,0）（-1,0）--（0，-1）（0,1）----(1,1)(-1,-1)---(-1, 1)(1, -1)
    def B_star_get_direct(self, cur):
        x_sub, y_sub = (self.end["point"][0] - cur[0]), (self.end["point"][1] - cur[1])
        # 说明 垂直 x轴上， k = y_sub / x_sub  0为被除数
        if x_sub == 0:
            # 除以绝对值
            return x_sub, y_sub / abs(y_sub)
        # 计算斜率
        k = y_sub / x_sub
        if 3 / 2 < k or k <= -3 / 2:
            if x_sub < 0:
                return (0, -1)
            else:
                return (0, 1)

        if 1 / 2 < k <= 3 / 2:
            if x_sub < 0:
                return (-1, -1)
            else:
                return (1, 1)

        if -1 / 2 < k <= 1 / 2:
            if x_sub < 0:
                return (-1, 0)
            else:
                return (1, 0)

        if -3 / 2 < k <= -1 / 2:
            if x_sub < 0:
                return (-1, 1)
            else:
                return (1, -1)