目录
一,点亮所有的灯
点击打开游戏 或者 资源分享汇总 里面的yo拼图,有各种拼图模式,其中翻转模式是点亮所有的灯的模式,这是我找到的唯一可以自由设置维度的点亮所有的灯小游戏。

规则:
游戏的棋盘可以多样化,本文只讨论n*n的棋盘。
每个格子有4个邻居(如果在边界就只有3个邻居,4角落只有2个邻居),
每个格子有2种状态,亮的或者黑的。
每次点击任意一个格子,它和它的4个邻居(不存在就不管了,下文不再重述)就会改变状态。
现在让你来进行一系列不限步数的点击(可以反复点击同一格子),使得所有的格子均点亮。
(我希望我已经描述完全清楚了,如果没有,请点击上面的链接,很好玩的游戏)
二,子问题性质
玩过魔方的人都知道,任何普通n(n>3)阶魔方都可以拼凑,转化成3阶魔方,最后用3阶魔方的方法复原。
虽然这肯定不是唯一方法,但是这是最有效的方法,玩n阶魔方的人几乎都是用这个方法。
但是这个问题有没有这么好的子问题性质呢?
很可惜,没有。只要稍微一想就知道,真的没有。
造成这种区别的关键是操作粒度的不同。魔方的操作粒度是任意的,可以转1层,可以转2层。。。
而本游戏中,操作是固定的(只有位置可选),操作给整个局面带来的影响也是固定的,都是与n无关的。
这个地方和N皇后问题很像:在一个N*N的棋盘上放置N个皇后,使其不能互相攻击。
如果你尝试把7皇后问题看成8皇后问题的子问题,那么,当这7个皇后放好了之后,第8个皇后就只能放在剩下的那一行剩下的那一列。没有选择的余地,很可能会因为对角线的冲突造成无解。
所以说,把7皇后问题看成8皇后问题的子问题是不可行的。本游戏亦如此。
三,术语定义
1,点操作:游戏规则中提到的操作,点击1个格子即为1次点操作
2,点状态:一个格子如果已经点亮(彩色的)那么称为好的状态,
如果未点亮(灰色的)那么称为坏的状态或者需要改变的状态。
3,行邻居:第i行的2个行邻居是第i-1行和第i+1行。如果i=1或者n,那么它就只有1个行邻居
4,(对第i(i<n)行进行的)往下行操作:对于第i行每个坏状态的格子,对在第i+1行中的那个邻居进行一次点操作。这样,第i行就复原了。
5,(对第i(i>1)行进行的)往上行操作:对于第i行每个坏状态的格子,对在第i-1行中的那个邻居进行一次点操作。这样,第i行就复原了。
6,全局操作:对n*n个格子中的每一个格子,要么就进行1次点操作,要么就不进行,这样的一系列操作称为1次全局操作。1个全局操作可以理解为1个大小为n*n的集合的子集,也可以理解为1个0-1矩阵。
7,中转状态:对于n阶的游戏的正确状态,依次对第1、2、3......n-1进行向下的行操作之后,除了第n行之外,肯定全部复原了。那么我们称此时的状态为中转状态。
8,可复原状态:经过若干次操作之后可以变成复原状态的状态,叫可复原状态,也叫正确状态。
四,解空间的结构
很显然解空间是一个复杂的图,而不是树,不过这个不是我们讨论的重点。
对于n*n的游戏,每个格子有2种状态,那么全局有2^(n*n)种状态。
这些状态中,不一定每个状态都是正确状态,所有的正确状态,按照一次转移定义的邻居,可以连成1个简单无向图,而且是连通的。
每个正确的状态都可以沿着某条路径转移到复原状态,对应的,复原状态也可以沿着这个路径转移到这个状态。
(以上皆为废话,重点来了)
这样的2条路径,方向相反但是边完全重合,他们对应的全局操作是完全一样的!
也就是说,对于一个可以复原的状态,如果它经过某个全局操作就复原了,那么对已经复原的状态再进行这个全局操作,又可以得到原本的全局操作。
PS:这其实是一个群。
五,全局状态、全局操作的关系
(1)
全局状态有2^(n*n)种,有些是可以复原的,有些是无法复原的。
全局操作也有2^(n*n)种,对于可以复原的状态,一定存在1个全局操作可以使得它复原。
对于无法复原的状态,一定不存在全局操作可以使得它复原。
对于已经复原的状态,进行任何一个全局操作,得到的皆为可以复原的操作。
所以说,存在一个十分自然的映射,从全局操作到全局状态的映射:
每个全局操作的映射结果为:复原状态经过这个全局操作得到的全局状态。
这个映射并不一定是双射,也就是说,可能有些全局操作是等价的,即2个全局操作对应同一个全局状态。
(2)
任何2个全局操作的叠加,得到的都是1个全局操作。
某些全局操作是等价的,比如:
01110 00000
10101 00000
11011 00000
10101 00000
01110 00000
这2个操作,显然是等价的。
所以,我们可以把所有的全局操作分成m个等价类。
神奇的是,不难证明,每个等价类的元素数目都是一样的,所以,m是2^(n*n)的约数。
假设m=2^k,那么每个等价类都有2^t个元素,其中t=n*n-k
这些等价类,和所有的正确状态,刚好可以一一映射。
进一步,不难推出,0<=t<=n,因为所有和0矩阵等价的矩阵都可以由第一行确定。
六,编程求解
对于一个正确的状态,如果用枚举法求出合适的全局操作,那效率非常低。
如果维度是6,那就要枚举2^36种全局操作,虽然中间会有很大剪枝,但是最后的效率还是很低。
因为我是在手机上玩这个游戏,所以可以先预处理一下,即化为中转状态。
这个时候再将最后一行的数据输入程序,输入也简单的多了。
这个时候来求合适的全局操作也很简单。
举例来说,如果n=3,那么全局操作一定是如下的形式:
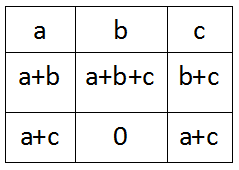
为什么只能是这个形式呢?
因为中转状态经过这个全局操作之后必须要复原,所以可以从上而下推导出这个表格。
所以我们只需要枚举第一行的a,b,c,找出满足条件的全局操作(一定是存在的)即可。
举例来说:

对于这个中转状态,向程序输入1,1,1,程序就需要解这样的一个方程组:
b+c=1,a+b+c=1,a+b=1
这里的加都是异或,或者说最后都要%2
这里的b+c、a+b+c、a+b的得到方法,和前面的表格是一样的。
编程解这个方程,可以用高斯消元法求解异或方程,也可以暴力枚举。
解出来a=0,b=1,c=0
也就是说,先点击第一行第一列的格子,然后现在这个状态,她的中转状态即为复原状态。
也就是说,点击第一行第一列的格子之后,依次对第1、2、3......n-1进行向下的行操作之后,一定就能得到复原状态。
现在,编程就变得十分简单了。
代码:
#include<iostream>
using namespace std;
int main()
{
int needlighten[10];
cout << "输入维度" << endl;
int n;//n阶点亮所有的灯
cin >> n;
cout << "点亮第1行,第2行。。。第" << n - 1;
cout << "行\n最后一行中,从左到右输入状态,1表示黑,0表示亮" << endl;
for (int nl = 0; nl<n; nl++) cin >> needlighten[nl];
int biao[12][12];
for (int number = 1; number<(1<<n); number++)
{
int num = number;
for (int k = 0; k<n; k++)
{
biao[1][k + 1] = num % 2;
num = num / 2;
}
for (int i = 0; i<n + 2; i++)for (int j = 0; j<n + 2; j++)
{
if (i == 0 || j == 0 || j == n + 1)biao[i][j] = 0;
else if (i != 1)biao[i][j] = (biao[i - 2][j] + biao[i - 1][j - 1] + biao[i - 1][j] + biao[i - 1][j + 1]) % 2;
}
bool buer = 1;
for (int u = 0; u<n; u++)if (biao[n + 1][u + 1] != needlighten[u])buer = 0;
if (buer)
{
cout << "点第一行的第";
for (int v = 0; v < n; v++)if (biao[1][v + 1])cout << v + 1 << " ";
cout << "个,再逐行完成即可";
}
if (buer)break;
}
system("pause > nul");
return 0;
}有了这个代码,这个游戏玩起来就十分简单了。
但是,这不代表这个游戏就没有研究的价值了,相反,还有非常有意思的事情是代码显示不了的。
POJ 3279 Fliptile
题目:
Description
Farmer John knows that an intellectually satisfied cow is a happy cow who will give more milk. He has arranged a brainy activity for cows in which they manipulate an M × N grid (1 ≤ M ≤ 15; 1 ≤ N ≤ 15) of square tiles, each of which is colored black on one side and white on the other side.
As one would guess, when a single white tile is flipped, it changes to black; when a single black tile is flipped, it changes to white. The cows are rewarded when they flip the tiles so that each tile has the white side face up. However, the cows have rather large hooves and when they try to flip a certain tile, they also flip all the adjacent tiles (tiles that share a full edge with the flipped tile). Since the flips are tiring, the cows want to minimize the number of flips they have to make.
Help the cows determine the minimum number of flips required, and the locations to flip to achieve that minimum. If there are multiple ways to achieve the task with the minimum amount of flips, return the one with the least lexicographical ordering in the output when considered as a string. If the task is impossible, print one line with the word "IMPOSSIBLE".
Input
Line 1: Two space-separated integers: M and N
Lines 2.. M+1: Line i+1 describes the colors (left to right) of row i of the grid with N space-separated integers which are 1 for black and 0 for white
Output
Lines 1.. M: Each line contains N space-separated integers, each specifying how many times to flip that particular location.
Sample Input
4 4
1 0 0 1
0 1 1 0
0 1 1 0
1 0 0 1Sample Output
0 0 0 0
1 0 0 1
1 0 0 1
0 0 0 0这个题目的意思是输入m,n,输入m*n的0-1矩阵,要求输出1个m*n的0-1矩阵。
除了尺寸不是正方形之外,其他的和我的描述都一样,输入全局状态(0-1矩阵),输出全局操作(0-1矩阵)
题目的意思是,如果有多个可行的方案的话,输出字典序最小的方案。
但是标程里面的字典序有问题,详情:点击打开链接

因为前面是针对我自己玩游戏的情况,而这里是针对ACM编程,所以,虽然是同样的问题,但是代码略有区别。
在这里,我用到了状态压缩,即用1个整数表示1行。
不过这样写出来的代码确实很难看懂,
f(k)表示的是,一个k代表的行操作对应的行增量,即对某一行进行k代表的行操作,那么这一行会有什么影响。
比如说,如果k代表的是a b c d e,那么对应的影响就是a+b a+b+c b+c+d c+d+e d+e
这个影响,可以看成3个影响的叠加:(1)a b c d e(2)b c d e 0(3)0 a b c d
状态压缩之后就是f里面的计算方法了。
代码:
#include<iostream>
using namespace std;
int m, n, a;
int l[17];
int temp[17];
int f(int k)
{
int t = (1 << n) - 1;
return (k * 2 ^ k^k / 2)&t;
}
bool ok(int k)
{
for (int i = 0; i < 17; i++)temp[i] = l[i];
temp[0] = k;
for (int i = 1; i < m; i++)
{
temp[i] = (temp[i] ^ f(temp[i - 1]));
temp[i + 1] = (temp[i + 1] ^ temp[i - 1]);
}
return temp[m]==f(temp[m-1]);
}
void out(int k)
{
for (int i = 0; i < 17; i++)temp[i] = l[i];
temp[0] = k;
for (int i = 1; i <= m; i++)
{
for (int j = 0; j < n; j++)
{
cout << (temp[i - 1] >> j) % 2;
if (j < n - 1)cout << " ";
}
cout << endl;





 本文围绕点亮所有灯的游戏展开,探讨了子问题性质、解空间结构等。介绍了编程求解方法,如用高斯消元法解异或方程。还对全局操作等价类进行分析,研究系数矩阵规律,包括对称、中心对称等,以及其形态、数值等方面规律。
本文围绕点亮所有灯的游戏展开,探讨了子问题性质、解空间结构等。介绍了编程求解方法,如用高斯消元法解异或方程。还对全局操作等价类进行分析,研究系数矩阵规律,包括对称、中心对称等,以及其形态、数值等方面规律。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2880
2880

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








