目录
〇,自我指涉
https://blog.youkuaiyun.com/nameofcsdn/article/details/104848261
一,谓词逻辑推理
1,推理过程的泛化
谓词逻辑推理,都可以泛化成这样的形式:
给出一些句子,每个句子都可以抽象成一个谓词公式(谓词公式包括原子谓词公式),根据语义+常识(公理)可以提炼出一些谓词公式之间的关系,再加上题目给的谓词公式之间的关系,推导出部分谓词公式的恒定值,或者关于这些谓词公式的某个代数式的最值等等。
PS:
谓词公式之间的关系可以有很多形式,比如若A则B,比如ABC里面至少有2个位true,比如若ABCDEFG里面至少有3个为true,则EFGH要么全true要么全false,等等等等。。。。
PS:
下文《三个人比大小》中有严格按照谓词逻辑的理论进行推理的示例。
2,谓词逻辑推理puzzle分类
按照输入条件的形式,可以分为普通逻辑、组合逻辑、自我指涉的逻辑。
这里的普通逻辑、组合逻辑都是非自我指涉的,而自我指涉的实际上又可以细分普通逻辑、组合逻辑等等。
组合逻辑中一种常见的特例,就是交叉逻辑。
二,普通逻辑
1,每个人一半真话一半假话
一天小明和小红,小黑后院玩耍,妈妈气冲冲地走过来,质问他们三个谁偷了放在柜子上面的一块钱。
小红说:我没偷,小黑没偷。
小黑说:小红没偷,我没偷。
小明说:我没偷,小红没偷。
已知他们所说的话中有一半是真一半是假,请问是谁偷了?
答案:
小红
2,三个人比大小
甲,乙,丙三人在酒吧摇筛子比点数大小。
甲:我的点数肯定比乙大
乙:我的点数是所有人里最大的
丙:我的点数是所有人里最大的。
只有一个人说了假话,请问三个人的大小关系?
答案:丙
泛化的求解思路:
(1)原子谓词公式
A表示甲>乙,B表示乙>甲,C表示乙>丙,D表示丙>甲,E表示丙>乙
(2)谓词公式
甲的谓词公式是x=A,乙的谓词公式是y=B&C,丙的谓词公式是z=D&E
“只有一个人说了假话”的谓词公式是(!x&y&z)|(x&!y&z)|(x&y&!z)
(3)谓词公式之间的关系
根据常识(公理)可得,A&B=false, C&E=false,
题目又说(!x&y&z)|(x&!y&z)|(x&y&!z)=true
(4)演算
因为x&y=A&B&C=false,y&z=B&C&D&E=false
又有(!x&y&z)|(x&!y&z)|(x&y&!z)=true
所以x=true,y=false,z=true
所以A=true,D=true,即丙>甲>乙。
3,两个人的成绩
小蓝和小黄是好朋友。
有一次,有人问她们‘你们谁的成绩好?’
小蓝说‘我的成绩比较好一些。’
小黄说‘我的成绩比较差一些。’
她们俩至少有一人没说实话。 那么到底谁的成绩好?(已知他们成绩不一样)
答案:小黄
三,交叉逻辑
仅以此游戏(交叉逻辑益智游戏)代表大量同类puzzle。
规则
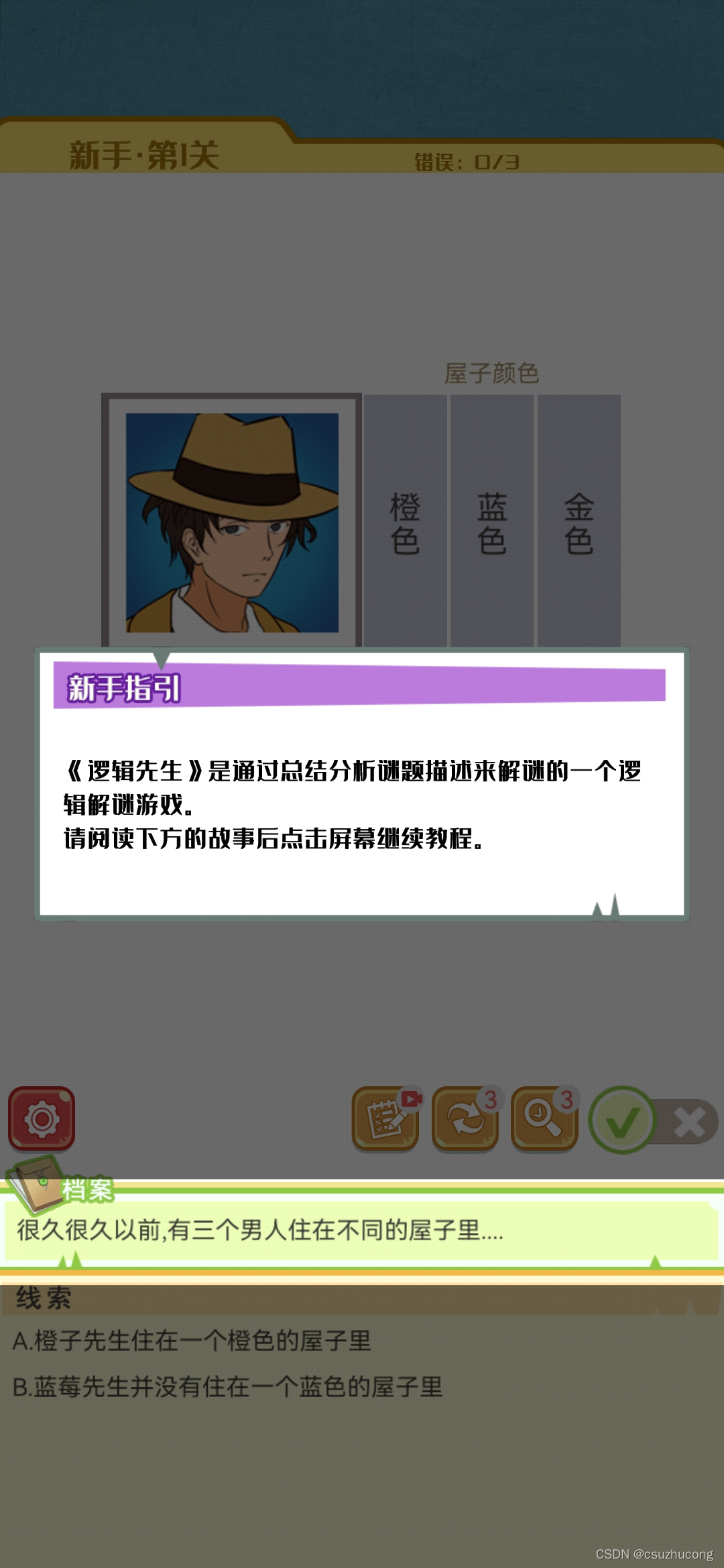
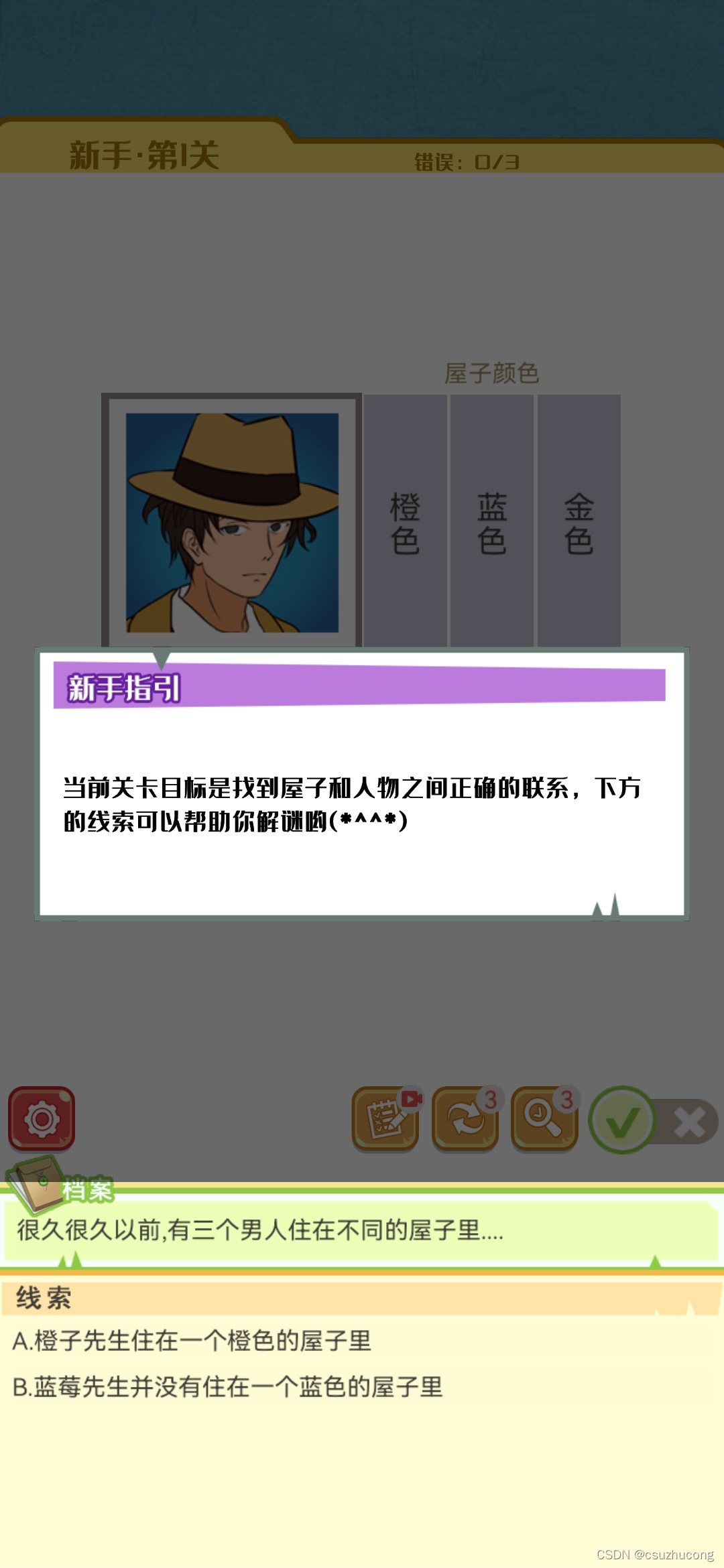
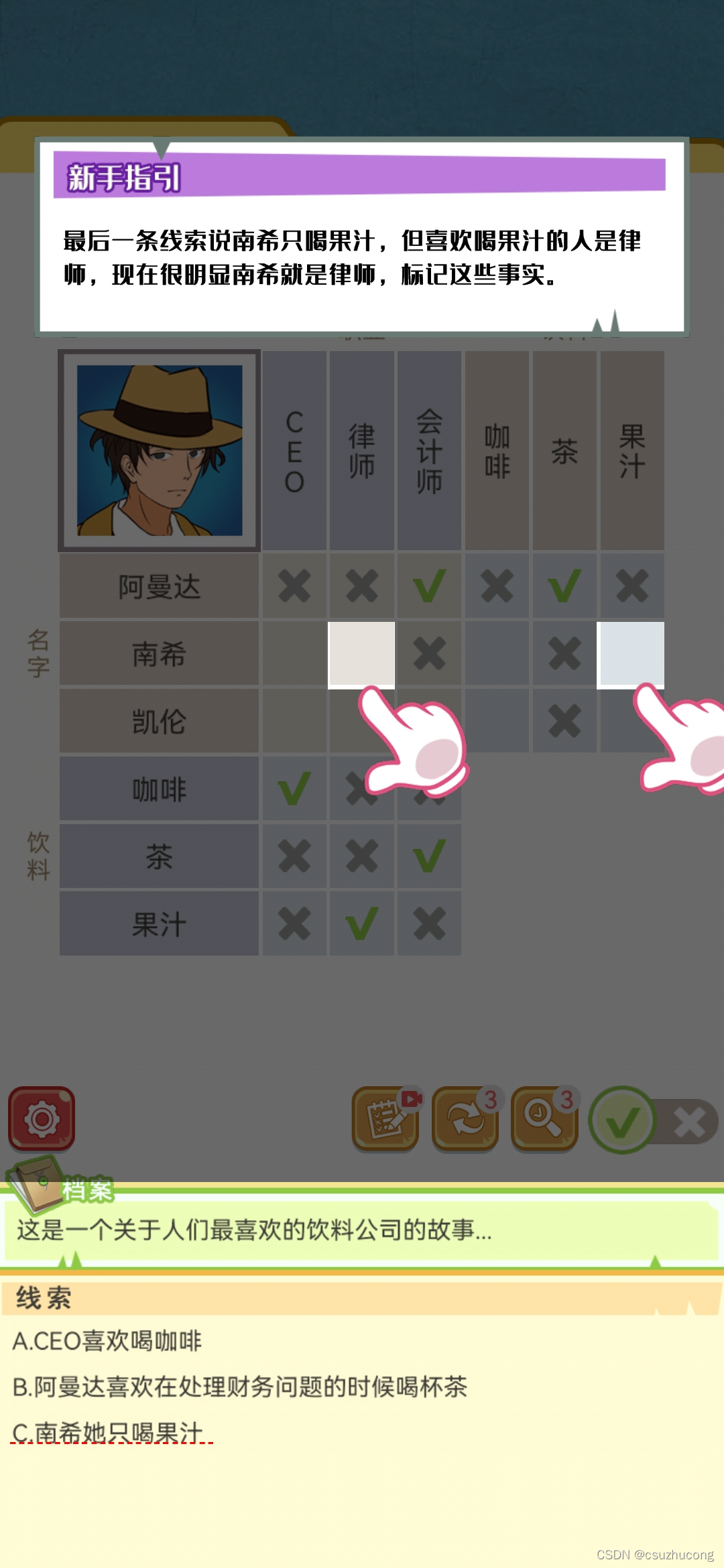
简单关卡
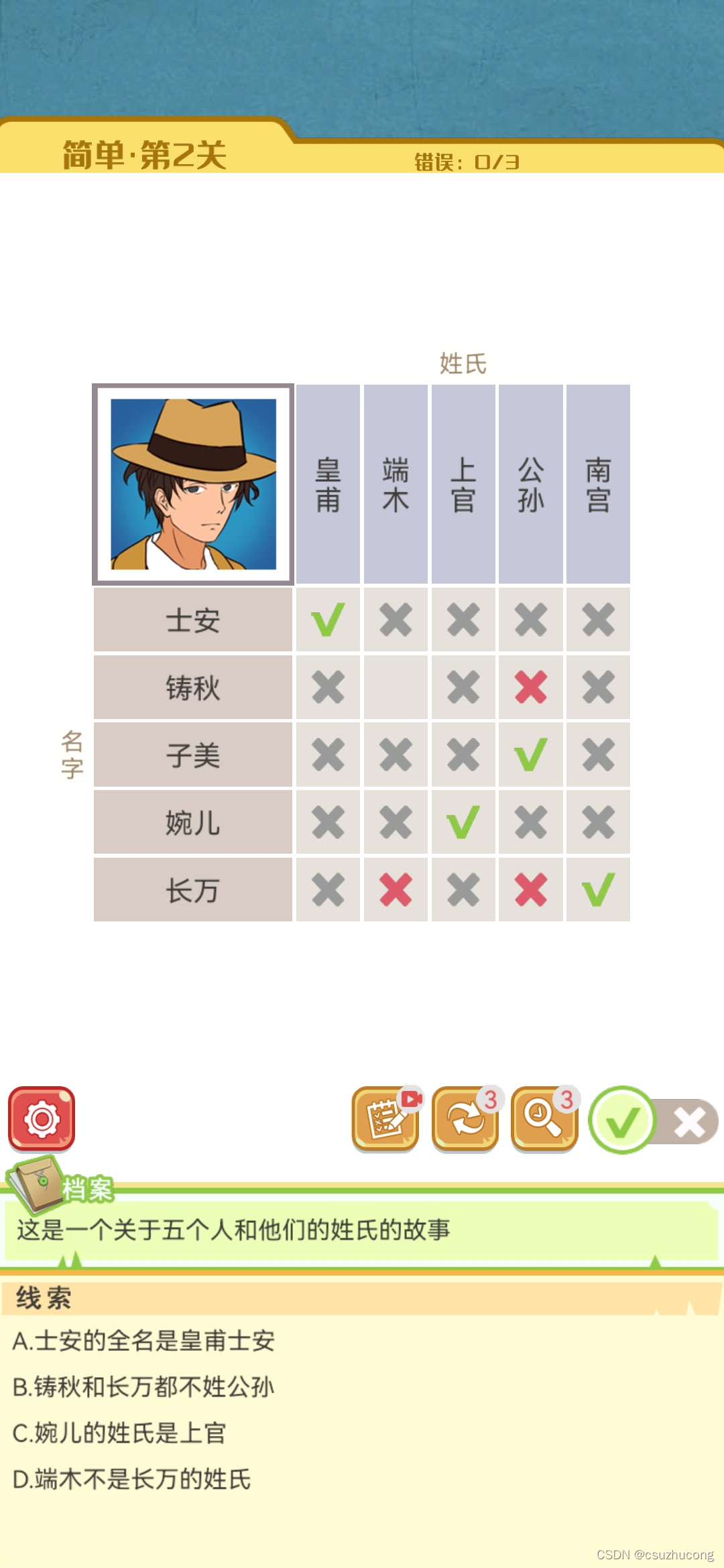
困难关卡


四,组合逻辑
1,宿舍人数
某宿舍住着若干个研究生,其中一个是黑龙江人,两个是北方人,一个是云南人, 两个人这学期只选修了逻辑哲学,三个人这学期选修古典音乐欣赏。
假设以上的介绍涉及了这宿舍中所有的人,那最少可能是几个人?最多可能是几个人?
答案:
最少5个,最多8个
五,自我指涉的逻辑
1,二难悖论
二难悖论参考经典悖论
2,二难推理
把不出现二难悖论作为条件的逻辑推理,叫二难推理,也叫自我指涉的逻辑推理。
二难推理大概分2大类,一类是和说真话说假话有关,一类是和选择题有关。这2类都可以用谓词逻辑去推理,比如当A为false时,“如果A则B”就是个真命题。
3,指涉环
真话假话问题,自我指涉的方式往往是,陈述内容形如“***是说真话的”,直接形成二难推理。
而选择题类的问题,自我指涉的方式往往是,A陈述内容形如“B陈述内容是错误的”,而B又指向C,C又指向A,从而形成环。
或者更长的环A->B->C->D->E->A
这个环越长,推理的难度往往越大。
4,真话假话问题
(1)这句话是谁说的
问题:
假如有2个人,一个叫小红一个叫小明,其中一个人一直说真话,另外一个人一直说假话。
有一天其中一个人说,“小红是一直说假话的那个人”,请问这句话是谁说的,是小红还是小明?
答案:
是小明,因为如果是小红说“小红是一直说假话的那个人”,那就构成了二难推理。
PS:我们还是不知道谁是说真话的人。
PS:说假话的那个人,无论他说“我是说假话的那个人”还是说“我这句话是假话”,都是二难推理。
(2)一个说真话的和一个说假话的人
如果有一个说真话的和一个说假话的人在一起,怎么样用1个是非问答题区分他们?
PS:每个人对提问都要尝试回答,回答的答案只涉及是和否,下同。
如果问,你是说真话的吗,或者问,你是说假话的吗?那么2人回答一致,无法区分。
如果问,你会回答否吗?那么说真话的人无法回答,说假话的人回答是或者否都可以。
(3)3个盒子
有红、绿、蓝三个盒子,其中只有一个盒子装有奖品。毎个盒子上有一句话。
红色盒子:奖品在蓝色盒子中。
绿色盒子:奖品不在红色盒子中。
蓝色盒子:奖品在绿色盒子中。
已知装有奖品的盒子上的话都是假话,没有奖品的盒子上的话都是真话。则奖品在哪个盒子中?
答案:
蓝色盒子
(4)三种人
这里所有人要么是只说真话的君子,要么是只说假话的小人,要么是有时说真话,有时说假话的凡夫。
其中等级从高到低君子,凡夫,小人。
a:我的等级不是最高的
b:我的等级比e高
c:b说的是对的
d:我和b的等级一样高
e:我不是等级最低的
f:g和a的等级一样高
g:h比我的等级高
h:我不比f的等级高
i:f比我的等级低或者我是个小人
已知gi不会都是凡夫,且这9个人里有且只有四个凡夫。那么b的身份是什么?
答案:
(1)我们推出a是凡夫。
(2)我们推出g是凡夫,f是君子或凡夫,i是君子或小人。
那么此时剩下还可以利用的信息只剩下:
b:我的等级比e高
c:b说的是对的
d:我和b的等级一样高
h:我不比f的等级高
i:f比我的等级低或者我是个小人
且这里只有四个凡夫。
(3)然后我们推出,f是凡夫,i是君子,h是凡夫。
那么此时剩下还可以利用的信息只剩下:
b:我的等级比e高
c:b说的是对的
d:我和b的等级一样高
且bcde中没有凡夫。
(4)最后我们推出,b是君子,c是君子,e是小人,d是君子或小人
那么此时所有信息都用完了,无矛盾。
(5)三种人三个问题
三个神A、B、C按乱序分别叫做「真实」、「错误」与「随机」。「真实」一直说真话,「错误」一直说假话,但是「随机」说真话或说假话是一件完全随机的事情。
你的任务是通过问3个是与非的问题来确认A、B和C的身份,每一个问题只能问一个神,不同问题可以选择同一个神。每个神只会回答「是」或者「否」。
答案:
问A:这个问题你会回答否吗?
问B:这个问题你会回答否吗?
如果其中有一个人无法回答,那么他就是「真实」,只要问他C是不是「错误」即可。
如果两个人都回答了,无论回答什么都没区别,C就是「真实」,只要问他A是不是「错误」即可。
PS:这个问题,其实是我根据下面的《有史以来最难的逻辑谜题》简化而来,而这个解答的思路也是我在解答《有史以来最难的逻辑谜题》时发现的思路,即想办法让神因为二难悖论而无法回答。
PS:这有点像“上帝啊,你既然说自己是万能的,那我问你,你能不能创造一个连你也搬不动的石头?”
(6)有史以来最难的逻辑谜题
这个谜题是 Smullyan留下的遗产,而这个标题是由麻省理工学院的逻辑哲学家George Boolos所写。
谜题:
三个神A、B、C按乱序分别叫做「真实」、「错误」与「随机」。「真实」一直说真话,「错误」一直说假话,但是「随机」说真话或说假话是一件完全随机的事情。
你的任务是通过问3个是与非的问题来确认A、B和C的身份,每一个问题只能问一个神,不同问题可以选择同一个神。这些神只会回答「da」或者「ya」,但你不知道哪个代表是,哪个代表否。
分析:
根据上面的二难悖论的思路,首先我们很容易想到这4种问题:
问题1:
你会回答「da」,而且「da」表示否,对吗?
如果「da」表示是,则「真实」会回答「ya」,「错误」会回答「da」, 「随机」回答哪个都可以
如果「da」表示否,则「真实」会无法回答, 「错误」回答哪个都可以,「随机」回答哪个都可以
问题2:
你会回答「da」,而且「da」表示是,对吗?
如果「da」表示是,则「真实」回答哪个都可以,「错误」会无法回答, 「随机」回答哪个都可以
如果「da」表示否,则「真实」会回答「da」, 「错误」会回答「ya」,「随机」回答哪个都可以
问题3:
你会回答「da」,而且你是「真实」对吗?
如果「da」表示是,则「真实」回答哪个都可以,「错误」会回答「da」,「随机」回答哪个都可以
如果「da」表示否,则「真实」会无法回答, 「错误」会回答「ya」,「随机」回答哪个都可以
问题4:
你会回答「da」,而且你是「错误」对吗?
如果「da」表示是,则「真实」会回答「ya」,「错误」会无法回答, 「随机」回答哪个都可以
如果「da」表示否,则「真实」会回答「da」,「错误」回答哪个都可以,「随机」回答哪个都可以
然后我们再看看,这4个问题选2个,能得到多少信息。
4个问题一共也就是16种组合,我简单分析了一下,应该是不足以推出答案。
于是我们还需要找出更复杂的问题才行。
问题5:
你是「真实」而且你会回答「da」,或者,你是「错误」而且你会回答「ya」,对吗?
如果「da」表示是,则「真实」回答哪个都可以,「错误」回答哪个都可以,「随机」回答哪个都可以
如果「da」表示否,则「真实」会无法回答, 「错误」会无法回答, 「随机」回答哪个都可以
问题6:
你是「真实」而且你会回答「ya」,或者,你是「错误」而且你会回答「da」,对吗?
如果「da」表示是,则「真实」会无法回答, 「错误」会无法回答, 「随机」回答哪个都可以
如果「da」表示否,则「真实」回答哪个都可以,「错误」回答哪个都可以,「随机」回答哪个都可以
问题7:
你是「真实」而且你会回答否,或者,你是「错误」而且你会回答是,对吗?
「真实」会无法回答, 「错误」会无法回答,「随机」回答哪个都可以
这样,我们终于想出了关键的问题,就是问题7
答案:
问A:你是「真实」而且你会回答否,或者,你是「错误」而且你会回答是,对吗?
问B:你是「真实」而且你会回答否,或者,你是「错误」而且你会回答是,对吗?
由于「真实」和「错误」都无法回答,「随机」回答哪个都可以,所以2次问答之后,就可以确定哪一个是「随机」
剩下的2个,随便选一个,问他:你会回答否,对吗?
由于「真实」会无法回答,「错误」回答哪个都可以,所以就区分开了。
5,选择题
选择题分为单选和多选2种。
单选中一种特殊的场景是判断题,可以理解成是2个选项的单选题,A选项是“...”,B选





 本文探讨了谓词逻辑推理的基本概念与方法,详细解析了自我指涉逻辑谜题,包括二难悖论、真话假话问题及选择题等,通过具体案例展示了逻辑推理的魅力。
本文探讨了谓词逻辑推理的基本概念与方法,详细解析了自我指涉逻辑谜题,包括二难悖论、真话假话问题及选择题等,通过具体案例展示了逻辑推理的魅力。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1004
1004

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








