已知在t−1时刻的数据rt−1,在预测t时刻rt时可能是有用的!
根据这点我们可以建立下面的模型:

其中{at}是白噪声序列,这个模型与简单线性回归模型有相同的形式,这个模型也叫做一阶自回归(AR)模型,简称AR(1)模型
从AR(1)很容易推广到AR(p)模型:

AR(p)模型的特征根及平稳性检验
我们先假定序列是弱平稳的,则有;

因为{at}是白噪声序列,因此有:

所以有:
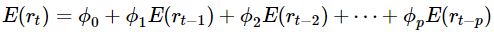
根据平稳性的性质,又有
 本文介绍了自回归AR(p)模型,包括AR(1)模型的定义,特征根与平稳性检验,以及如何通过偏相关函数和信息准则(AIC、BIC、HQ)进行模型定阶。同时,讨论了模型的检验、拟合优度评估以及预测方法,强调了防止过拟合的重要性。
本文介绍了自回归AR(p)模型,包括AR(1)模型的定义,特征根与平稳性检验,以及如何通过偏相关函数和信息准则(AIC、BIC、HQ)进行模型定阶。同时,讨论了模型的检验、拟合优度评估以及预测方法,强调了防止过拟合的重要性。
已知在t−1时刻的数据rt−1,在预测t时刻rt时可能是有用的!
根据这点我们可以建立下面的模型:

其中{at}是白噪声序列,这个模型与简单线性回归模型有相同的形式,这个模型也叫做一阶自回归(AR)模型,简称AR(1)模型
从AR(1)很容易推广到AR(p)模型:

我们先假定序列是弱平稳的,则有;

因为{at}是白噪声序列,因此有:

所以有:
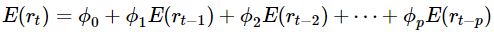
根据平稳性的性质,又有
您可能感兴趣的与本文相关的镜像

Qwen3-8B
Qwen3 是 Qwen 系列中的最新一代大型语言模型,提供了一整套密集型和专家混合(MoE)模型。基于广泛的训练,Qwen3 在推理、指令执行、代理能力和多语言支持方面取得了突破性进展
 1393
1393
 6415
6415

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


