从内外参推导IPM变换方程及代码实现（生成AVM环视拼接图）

一、前言

最近想实现AVM拼接，看了不少博客和论文，不过比较愚钝，一直没能很好理解原理，尤其是怎么在实现时把下文式1与式2中Z1和Z2消除的，所以严谨的推导了一下对应的公式，如有不对，水平有限，烦请指出~

IPM变换（逆透视变换），顾名思义，即将正常透视效应消除的变换，变换结果为鸟瞰图BEV（俯视图）；AVM环视拼接一般是将车身前后左右的四个鱼眼相机拼接成环视图（也是俯视），其使用的单应矩阵将四个相机转到同一个俯视坐标系。

投影变换的通俗理解就是：假设同一个相机分别在A、B两个不同位置，以不同的位姿拍摄同一个平面（重点是拍摄平面，例如桌面、墙面、地平面），生成了两张图象，这两张图象之间的关系就叫做投影变换。

二、公式推导

公式太难打了，全用word存了，在这直接截图

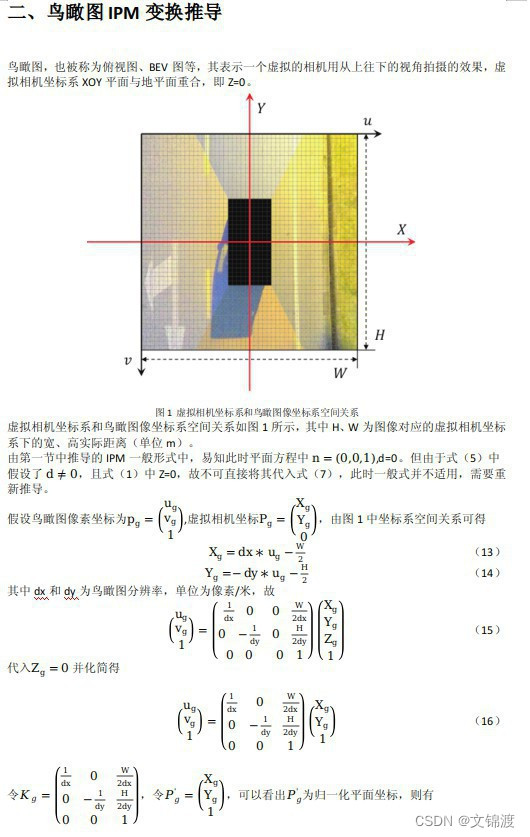
这也就解释了：为什么有的AVM算法是需要标定相机的内外参，而有的只提供单应矩阵H。

 三、示例代码

#include <Eigen/Core>
#include <Eigen/Dense>
#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/core/eigen.hpp>
#include <opencv2/opencv.hpp>
#include <vector>

void DistortEigenPoints(const Eigen::Vector3d &undis_pt, Eigen::Vector3d &dis_pt, double k1, double k2, double p1,
                        double p2) {
    double x2 = undis_pt[0] * undis_pt[0];
    double y2 = undis_pt[1] * undis_pt[1];
    double r2 = x2 + y2;
    if (r2 == 0) return;

    double r4 = r2 * r2;
    double r6 = r2 * r4;
    double xy = undis_pt[0] * undis_pt[1];
    dis_pt[0] = undis_pt[0] * (1 + k1 * r2 + k2 * r4) + 2 * p1 * xy + p2 * (r2 + 2 * x2);
    dis_pt[1] = undis_pt[1] * (1 + k1 * r2 + k2 * r4) + p1 * (r2 + 2 * y2) + 2 * p2 * xy;
    dis_pt[2] = 1;
    return;
}

float interp(const cv::Mat &img, float x, float y) {
    int ix = x;
    int iy = y;

    float dx = x - ix;
    float dy = y - iy;

    float ddx = 1.0f - dx;
    float ddy = 1.0f - dy;
    return ddx * ddy * img.data[iy * img.cols + ix] + ddx * dy * img.data[(iy + 1) * img.cols + ix] +
           dx * ddy * img.data[iy * img.cols + ix + 1] + dx * dy * img.data[(iy + 1) * img.cols + ix + 1];
}

int main() {
    std::string img_path = "Mynt/00001772.jpg";
    Eigen::Matrix3d K_c;
    K_c << 1037.536376953125, 0, 600.182861328125, 0, 1038.532958984375, 358.40493774414062500, 0, 0, 1;
    double k1 = 0.03784750;
    double k2 = -0.051872;
    double p1 = -0.000938;
    double